Нервная система выполняет ряд важных функций:
- обеспечивает связь организма с окружающим миром;
- управляет работой всех органов;
- координирует функционирование всех систем органов, обеспечивая их согласованную работу.
Нервная ткань
Нервная ткань отличается от других тканей нашего организма тем, что обладает особыми свойствами — возбудимостью и проводимостью. Эти свойства нервной ткани обусловлены особенностями её строения.
В состав нервной ткани входят клетки двух видов. Основные функции выполняют нейроны, а клетки-спутники (клетки нейроглии) служат опорой и обеспечивают обмен веществ.
Рис. (1). Нервная ткань
Функции нейронов: генерирование и передача нервных импульсов; обработка и хранение поступающей информации.
Нервный импульс — это волна возбуждения (биоэлектрическая волна), распространяющаяся по нервным клеткам.
Нейрон — основная клетка нервной ткани. Он имеет тело и отростки двух типов. В теле нейрона располагается ядро и органоиды, а по отросткам передаются нервные импульсы.
Дендриты — это отростки, по которым нервные импульсы передаются к телу нейрона. Эти отростки сильно ветвятся. У нейрона может быть несколько дендритов.
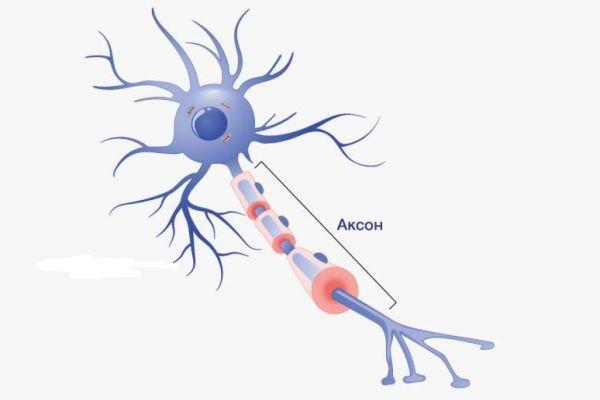
Аксон — это отросток, по которому импульсы передаются от тела клетки. Аксон обычно ветвится только на конце. У каждого нейрона всего один аксон.
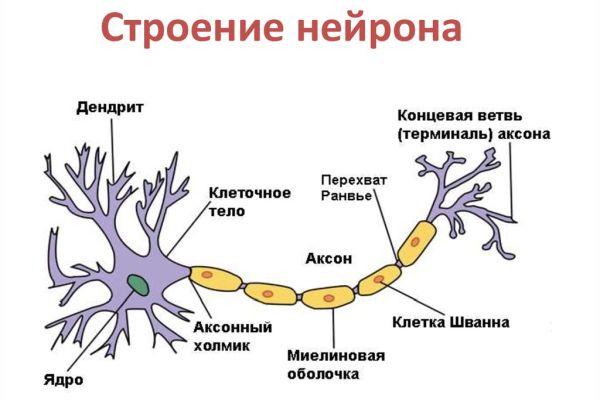
Рис. (2). Строение нейрона
Аксоны часто окружены оболочкой из жироподобного вещества миелина. Это вещество имеет белый цвет. Скопления миелинизированных аксонов образуют белое вещество головного и спинного мозга. Тела нервных клеток и дендриты не покрыты миелином. Они серого цвета, а их группы составляют серое вещество центральной нервной системы.
Передача нервных импульсов с одной клетки на другую происходит в синапсах.
Синапс — это место контакта между двумя нейронами или между нейроном и клеткой рабочего органа.
Главными элементами синапса являются мембраны двух клеток (пресинаптическая и постсинаптическая мембраны) и пространство между ними (синаптическая щель).
Рис. (3). Строение синапса
В аксоне пресинаптического нейрона вырабатывается медиатор — особое вещество, с помощью которого происходит передача нервного импульса.
Под действием нервного импульса медиатор выделяется в синаптическую щель. Рецепторы постсинаптической мембраны реагируют на его появление и генерируют возникновение нервного импульса в следующем нейроне. Так в синапсе происходит химическая передача возбуждения с одной клетки на другую.
Нейроны различаются по своему строению и выполняемым функциям.
Рис. (4). Виды нейронов
По выполняемым функциям выделяют три типа нейронов.
Чувствительные (сенсорные) нейроны проводят информацию от органов в мозг. Тела таких нейронов находятся в нервных узлах вне центральной нервной системы.
Другая группа нейронов передаёт информацию от головного и спинного мозга к органам. Это двигательные (моторные) нейроны. Их тела находятся в сером веществе центральной нервной системы, а аксоны находятся за пределами ЦНС.
Третий вид нейронов осуществляет связь между чувствительными и двигательными нейронами. Это вставочные нейроны, они находятся в головном и спинном мозге.
Скопление нейронов в головном или спинном мозге называют ядром.
Рис. (5). Типы нейронов и синапсы
Связь между органами и центральной нервной системой осуществляется через нервы.
Нерв — это орган, в состав которого входят пучки нервных волокон, покрытые соединительнотканной оболочкой.
Рис. (6). Нерв
Нервы выполняют проводниковую функцию. Они связывают головной и спинной мозг с кожей, органами чувств и с внутренними органами.
Нервы бывают чувствительные, двигательные и смешанные.
Чувствительные нервы проводят нервные импульсы от рецепторов в мозг. В их состав входят дендриты чувствительных нейронов.
Двигательные нервы состоят из аксонов двигательных нейронов. Их функция — проведение импульсов от мозга к рабочим органам.
Смешанные нервы образованы чувствительными и двигательными волокнами и способные проводить импульсы как к ЦНС, так и от ЦНС.
Нервные сплетения представлены сетчатыми скоплениями нервных волокон разных нервов, связывающих ЦНС с внутренними органами, скелетными мышцами и кожей.
Наиболее известное солнечное сплетение находится в брюшной полости.
Источники:
Рис. 1. Нервная ткань https://image.shutterstock.com/image-photo/mammalian-nervous-tissue-under-microscope-600w-74170234.jpg
Рис. 2. Строение нейрона https://image.shutterstock.com/image-vector/education-chart-biology-nerve-cell-600w-661087429.jpg
Рис. 3. Строение синапса https://image.shutterstock.com/image-illustration/gap-between-two-nerve-cells-600w-1284912691.jpg
Рис. 4. Виды нейронов https://image.shutterstock.com/image-illustration/different-kinds-neurons-scheme-structure-600w-138356969.jpg
Рис. 5. Типы нейронов и синапсы © ЯКласс
Рис. 6. Нерв https://image.shutterstock.com/image-illustration/nerve-structure-anatomy-600w-1041115012.jpg
Нервная ткань — основная ткань, формирующая нервную систему и создающая условия для реализации ее многочисленных функций. Нервная ткань имеет эктодермальное происхождение, не принято делить нервную ткань на какие-либо виды тканей. Обладает двумя основными свойствами: возбудимостью и проводимостью.
Нейрон
Структурно-функциональной единицей нервной ткани является нейрон (от др.-греч. νεῦρον — волокно, нерв) — клетка с одним
длинным отростком — аксоном (греч. axis — ось), и одним/несколькими короткими — дендритами (греч. dendros — дерево).
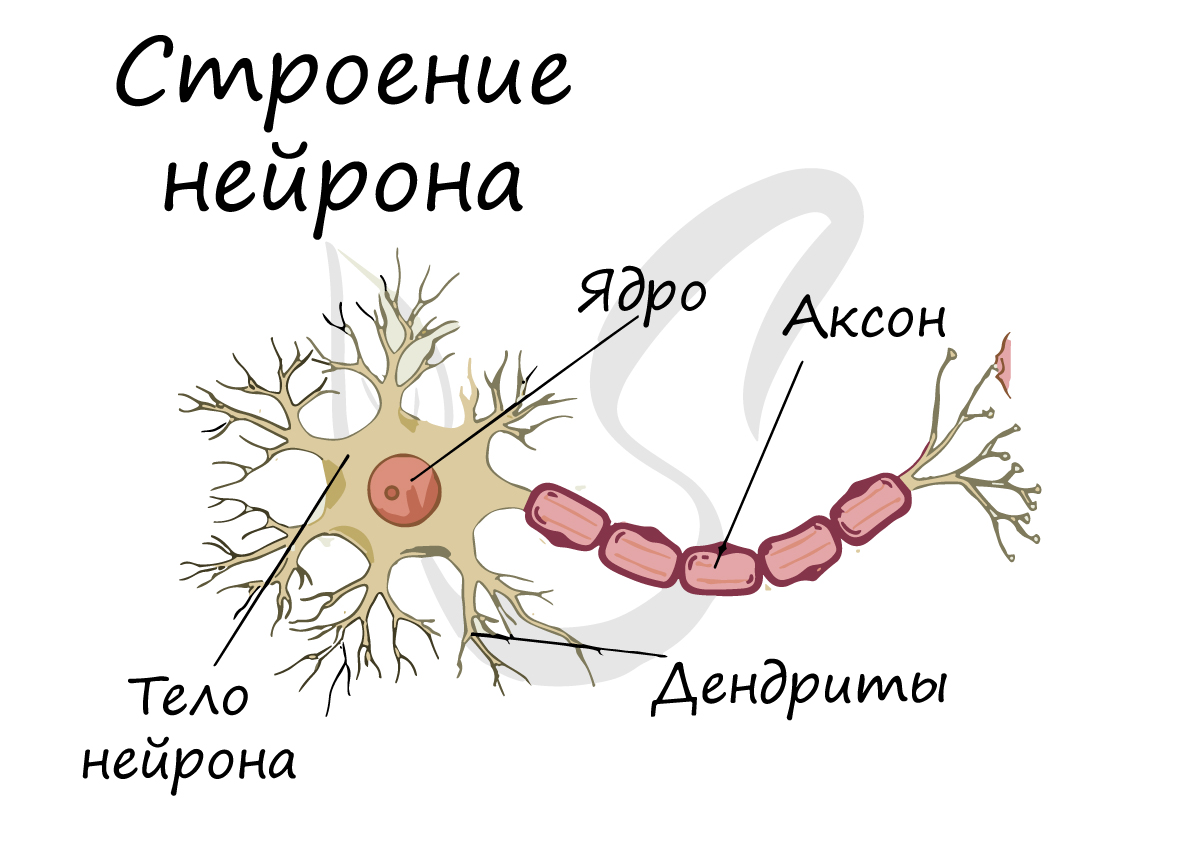
Спешу сообщить, что представление, будто короткий отросток нейрона — всегда дендрит, а длинный — всегда аксон, в корне неверно. С точки
зрения физиологии правильнее дать следующие определения: дендрит — отросток нейрона, по которому нервный импульс перемещается к телу нейрона, аксон — отросток нейрона, по которому импульс перемещается от тела нейрона.
Нейроны обладают 4 свойствами:
- Рецепция (лат. receptio — принятие) — способны воспринимать поступающие сигналы (дендриты)
- В ответ на сигналы способны переходить в состояние возбуждения или торможения
- Проведение возбуждения (от дендрита к телу нейрона, затем — к концу аксона)
- Передача сигнала другим объектам — нейрону или эффекторному органу
В физиологии эффекторным (от лат. efferes — выносящий) органом часто называют исполнительный орган или орган-мишень воздействия (мышцы, железы). Орган-эффектор выполняет те или иные «приказы» ЦНС (центральной нервной системы) или эндокринных желёз
Отростки нейронов проводят нервные импульсы и передают их другим нейронам, эффекторам, благодаря чему
мышцы сокращаются или расслабляются, а секреция желез усиливается или уменьшается.
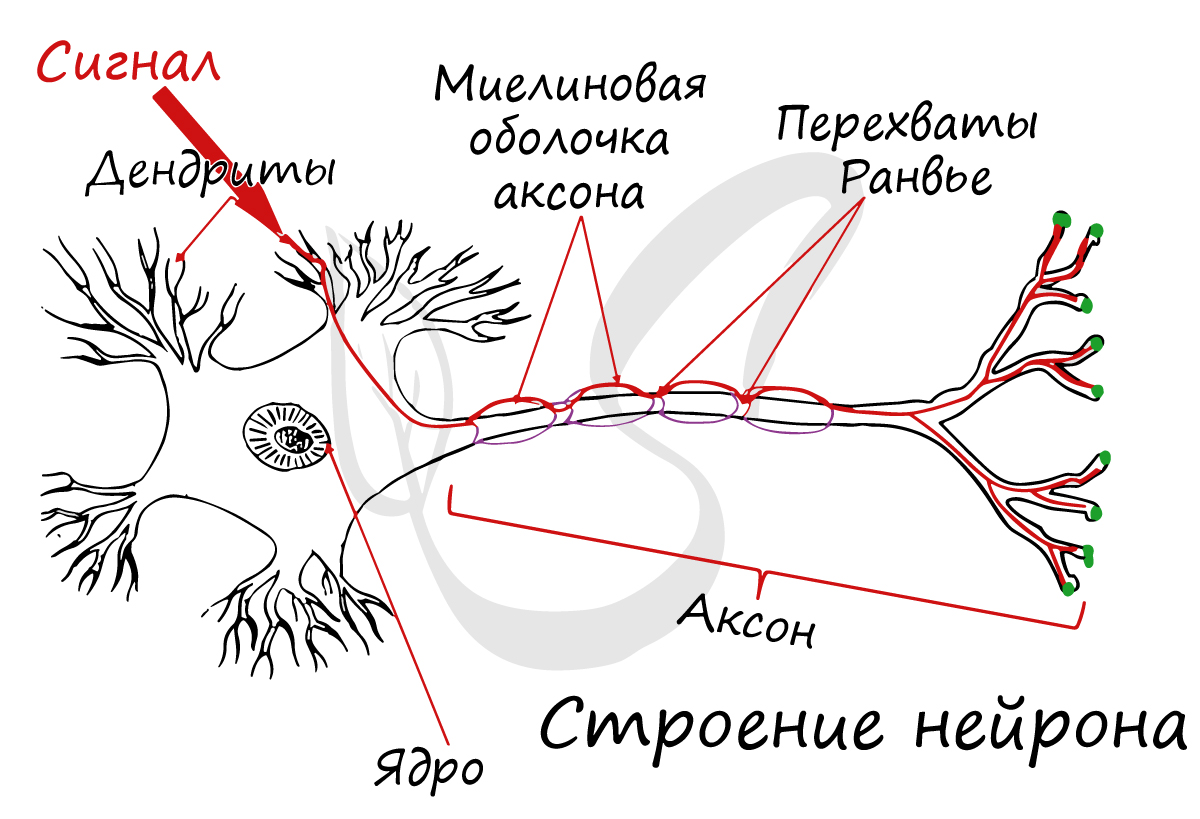
Миелиновая оболочка
Нервные волокна подразделяются на миелиновые и безмиелиновые. Нервное волокно — это один или несколько отростков нейронов (могут быть как аксоны, так и дендриты) с окружающей оболочкой.
Безмиелиновые нервные волокна находятся преимущественно в составе вегетативной нервной системы (скорость проведения 1-2 м/c). Миелиновые — образуют белое вещество головного и спинного мозга, нервные волокна соматической нервной системы (5-120 м/с).
В миелиновых нервных волокнах отростки нейронов покрыты миелиновой оболочкой (на 70-75% состоит из липидов (жиров)), которая обеспечивает изолированное проведение нервного
импульса по нерву. Если бы не было миелиновой оболочки (вообразите!) нервные импульсы распространялись бы хаотично, и,
когда мы хотели сделать движение рукой, то вместе с рукой двигалась бы нога.
Существует болезнь при которой собственные антитела уничтожают миелиновую оболочку нервных волокон головного и спинного мозга (случаются и такие сбои в работе организма). Эта
болезнь — рассеянный склероз, по мере прогрессирования приводит к разрушению не только миелиновой оболочки, но и нервов — а значит,
происходит атрофия мышц и человек постепенно становится обездвиженным.

Миелиновый слой представлен несколькими слоями мембраны глиальной клетки (леммоцит, шванновская клетка), которые закручиваются вокруг осевого цилиндра (отростка нейрона). Это закручивание хорошо видно на картинке, где изображен здоровый нерв, чуть выше 
Миелиновый слой оболочки волокна регулярно прерывается в местах стыка соседних леммоцитов — перехваты Ранвье. Миелиновая оболочка обеспечивает изолированное и более быстрое проведение возбуждения (сальтаторный тип, лат. salto — скачу, прыгаю).

Нейроглия (греч. νεῦρον — волокно, нерв + γλία — клей)
Вы уже убедились, насколько значимы нейроны, их высокая специализация приводит к возникновению особого окружения — нейроглии.
Нейроглия (глиальные клетки, глиоциты) — вспомогательная часть нервной системы, которая выполняет ряд важных функций:
- Опорная — поддерживает нейроны в определенном положении
- Регенераторная (лат. regeneratio — возрождение) — в случае повреждения нервных структур нейроглия способствует регенерации
- Трофическая (греч. trophe — питание) — с помощью нейроглии осуществляется питание нейронов: напрямую с кровью нейроны не контактируют
- Электроизоляционная — леммоциты (шванновские клетки) закручиваются вокруг отростков нейронов и формируют миелиновую оболочку
- Барьерная и защитная — изолируют нейроны от тканей внутренней среды организма
- Некоторые глиоциты секретируют цереброспинальную (спинномозговую) жидкость — ликвор (от лат. liquor — жидкость)
В состав нейроглии входят разные клетки, их в десятки раз больше чем самих нейронов. В периферическом отделе нервной
системы миелиновая оболочка, изученная нами, образуется именно из нейроглии — шванновских клеток (леммоцитов). Между ними хорошо
заметны перехваты Ранвье — участки, лишенные миелиновой оболочки, между двумя смежными шванновскими клетками.
Классификация нейронов
Нейроны функционально подразделяются на чувствительные, двигательные и вставочные.
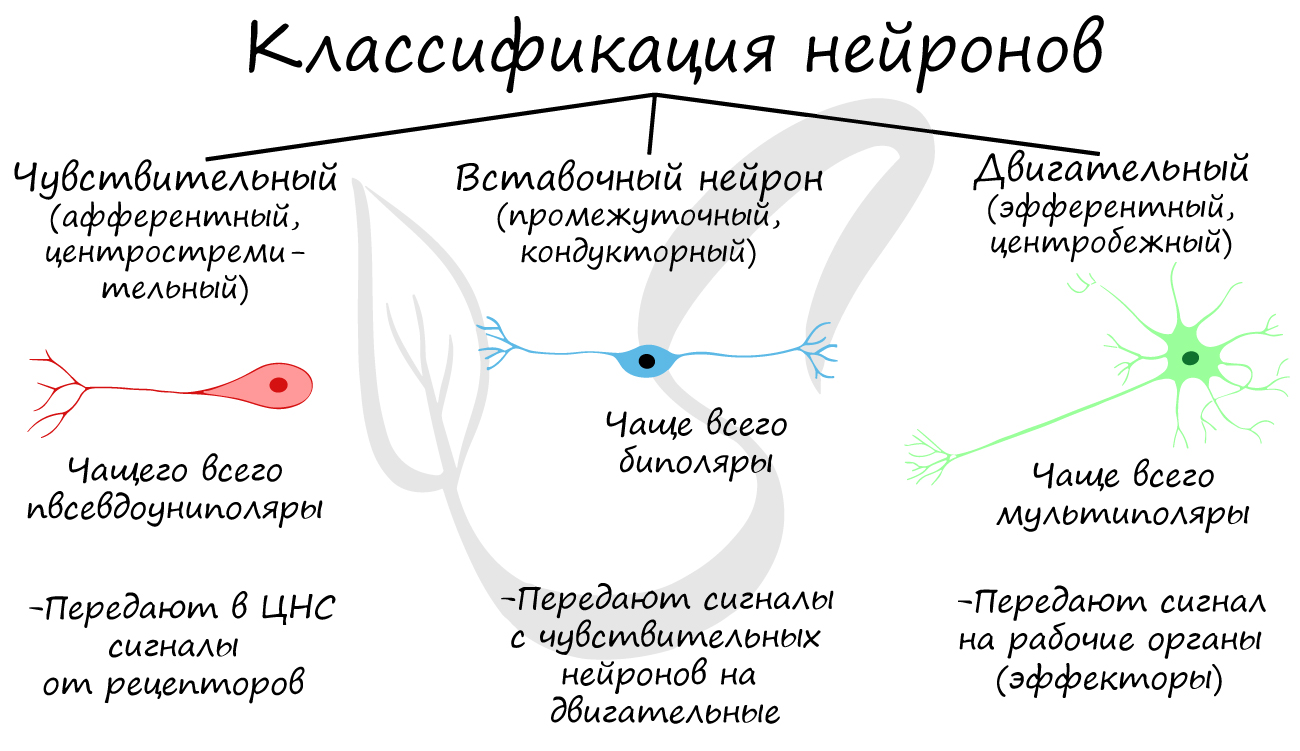
Чувствительные нейроны также называются афферентные, центростремительные, сенсорные, воспринимающие — они воспринимают раздражения, преобразуют их в нервные импульсы и передают в ЦНС. Рецептором называют концевое окончание чувствительных нервных
волокон, воспринимающих раздражитель.
Вставочные нейроны также называются промежуточные, ассоциативные — они обеспечивают связь между чувствительными и двигательными
нейронами, передают возбуждение в различные отделы ЦНС, участвуют в обработке информации и выработке команд.
Двигательные нейроны по-другому называются эфферентные, центробежные, мотонейроны — они передают нервный импульс (возбуждение) на
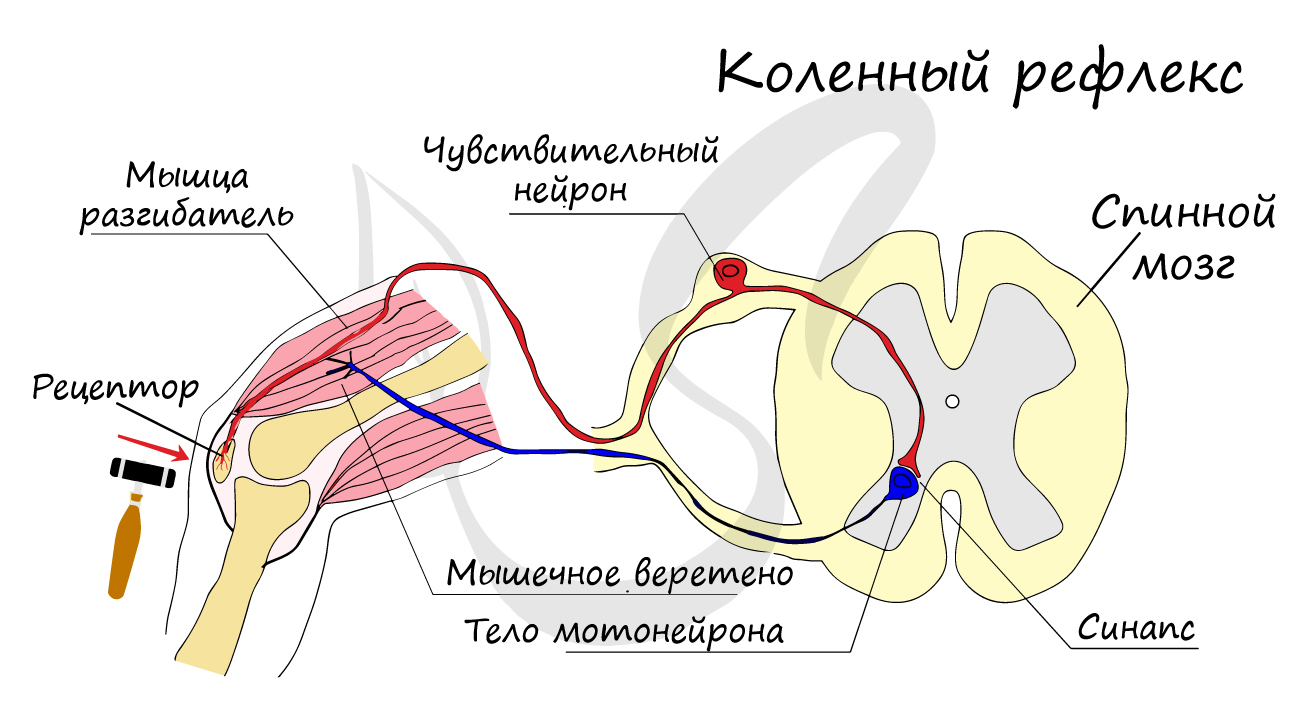
эффектор (рабочий орган). Наиболее простой пример взаимодействия нейронов — коленный рефлекс (однако вставочного нейрона
на данной схеме нет). Более подробно рефлекторные дуги и их виды мы изучим в разделе, посвященном нервной системе.
Синапс
На схеме выше вы наверняка заметили новый термин — синапс (греч. sýnapsis — соединение). Синапсом называют место контакта между двумя нейронами или между
нейроном и эффектором (органом-мишенью). В синапсе нервный импульс «преобразуется» в химический: происходит выброс особых
веществ — нейромедиаторов (наиболее известный — ацетилхолин) в синаптическую щель.
Разберем строение синапса на схеме. Его составляют пресинаптическая мембрана аксона, рядом с которой расположены везикулы (лат. vesicula — пузырек) с
нейромедиатором внутри (ацетилхолином). Если нервный импульс достигает терминали (окончания) аксона, то везикулы начинают
сливаться с пресинаптической мембраной: ацетилхолин поступает наружу, в синаптическую щель.
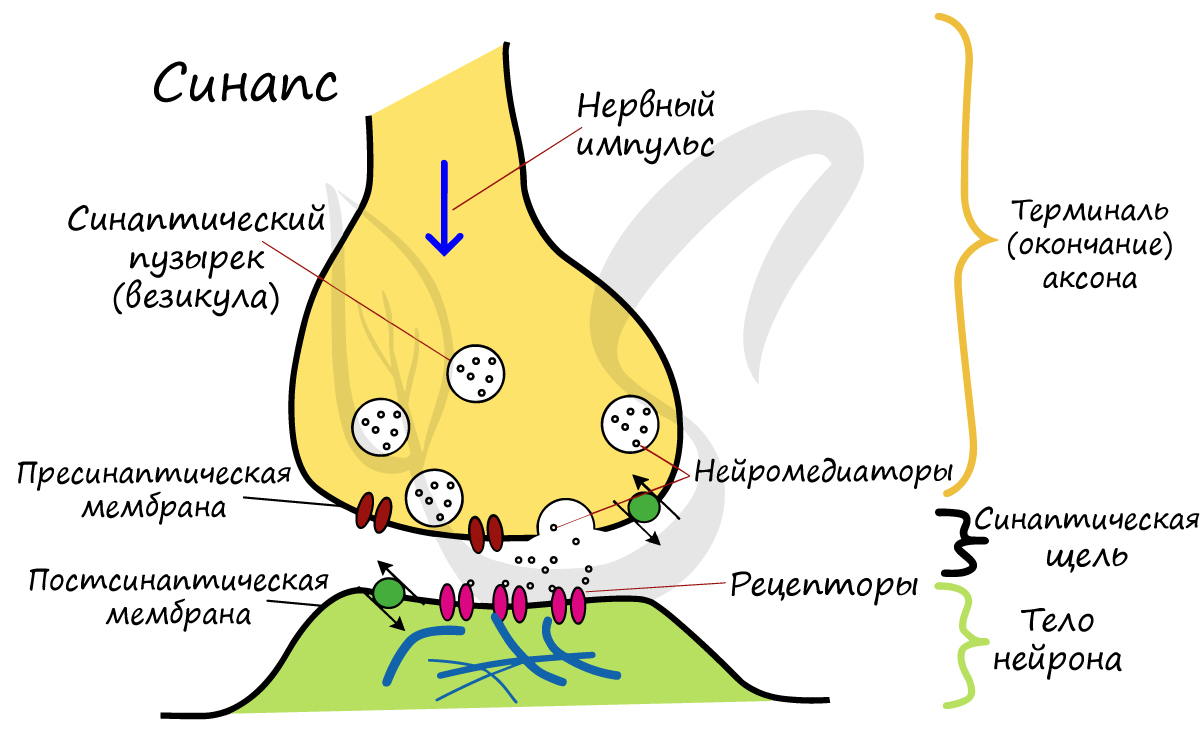
Попав в синаптическую щель, ацетилхолин связывается с рецепторами на постсинаптической мембране, таким образом, возбуждение (нервный импульс)
передается другому нейрону. Так устроена нервная система: электрический путь передачи сменяется
химическим (в синапсе).
Яд кураре
Гораздо интереснее изучать любой предмет на примерах, поэтому я постараюсь как можно чаще радовать вас ими 
историю о яде кураре, который используют индейцы для охоты с древних времен.
Этот яд блокирует ацетилхолиновые рецепторы на постсинаптической мембране, и, как следствие, химическая передача возбуждения с
одного нейрона на другой становится невозможна. Это приводит к тому, что нервные импульсы перестают поступать к эффекторам,
в том числе к дыхательным мышцам (межреберным, диафрагме), вследствие чего дыхание останавливается и наступает смерть животного.

Нервы и нервные узлы
Собираясь вместе, отростки нейронов (нервные волокна) образуют пучки нервных волокон. Нервные пучки объединяются в нервы, которые покрыты соединительнотканной оболочкой.
В случае, если тела нейронов концентрируются в одном месте за пределами центральной нервной системы, их скопления
называют нервным узлом — или ганглием (от др.-греч. γάγγλιον — узел).
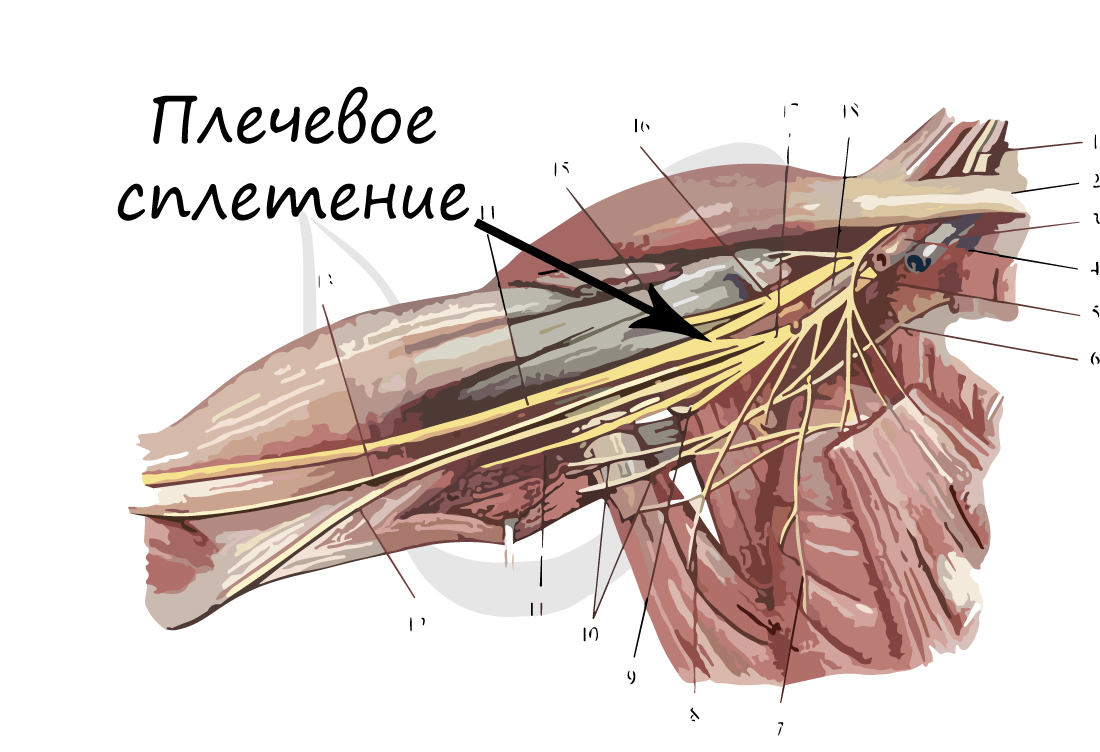
В случае сложных соединений между нервными волокнами говорят о нервных сплетениях. Одно из наиболее известных —
плечевое сплетение.
Болезни нервной системы
Неврологические болезни могут развиваться в любой точке нервной системы: от этого будет зависеть клиническая картина. В случае повреждения
чувствительного пути пациент перестает чувствовать боль, холод, тепло и другие раздражители в зоне иннервации пораженного нерва, при этом
движения сохранены в полном объеме.
Если повреждено двигательное звено, движение в пораженной конечности будет
невозможно: возникает паралич, но чувствительность может сохраняться.
Существует тяжелое мышечное заболеванием — миастения (от др.-греч. μῦς — «мышца» и ἀσθένεια — «бессилие, слабость»), при
котором собственные антитела разрушают мотонейроны (двигательные нейроны).

Постепенно любые движения мышцами становятся для пациента все труднее,
становится тяжело долго говорить, повышается утомляемость. Наблюдается характерный симптом — опущение верхнего века.
Болезнь может привести к слабости диафрагмы и дыхательных мышц, вследствие чего дыхание становится невозможным.
© Беллевич Юрий Сергеевич 2018-2023
Данная статья написана Беллевичем Юрием Сергеевичем и является его интеллектуальной собственностью. Копирование, распространение
(в том числе путем копирования на другие сайты и ресурсы в Интернете) или любое иное использование информации и объектов
без предварительного согласия правообладателя преследуется по закону. Для получения материалов статьи и разрешения их использования,
обратитесь, пожалуйста, к Беллевичу Юрию.
|
|
Макеты страниц
Часть I. ТЕОРИЯ
Глава 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
Под нейронными сетями подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Они представляют собой распределенные и параллельные системы, способные к адаптивному обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом.
К настоящему времени предложено и изучено большое количество моделей нейроподобных элементов и нейронных сетей, ряд из которых рассмотрен в настоящей главе.
1.1. Биологический нейрон
Нервная система и мозг человека состоят из нейронов, соединенных между собой нервными волокнами. Нервные волокна способны передавать электрические импульсы между нейронами. Все процессы передачи раздражений от кожи, ушей и глаз к мозгу, процессы мышления и управления действиями — все это

Рис. 1.1 Взаимосвязь биологических нейронов
реализовано в живом организме как передача электрических импульсов между нейронами.
Нейрон (нервная клетка) является особой биологической клеткой, которая обрабатывает информацию (рис. 1.1). Он состоит из тела (cell body), или сомы (soma), и отростков нервных волокон двух типов — дендритов (dendrites), по которым принимаются импульсы, и единственного аксона (ахоп), по которому нейрон может передавать импульс. Тело нейрона включает ядро (nucleus), которое содержит информацию о наследственных свойствах, и плазму, обладающую молекулярными средствами для производства необходимых нейрону материалов. Нейрон получает сигналы (импульсы) от аксонов других нейронов через дендриты (приемники) и передает сигналы, сгенерированные телом клетки, вдоль своего аксона (передатчика), который в конце разветвляется на волокна (strands). На окончаниях этих волокон находятся специальные образования — синапсы (synapses), которые влияют на величину импульсов.
Синапс является элементарной структурой и функциональным узлом между двумя нейронами (волокно аксона одного нейрона и дендрит другого). Когда импульс достигает синаптического окончания, высвобождаются химические вещества, называемые нейротрансмиттерами. Нейротрансмиттеры диффундируют через синаптическую щель, возбуждая или затормаживая, в зависимости от типа синапса, способность нейрона-приемника генерировать
электрические импульсы Результативность передачи импульса синапсом может настраиваться проходящими через него сигналами так, что синапсы могут обучаться в зависимости от активности процессов, в которых они участвуют. Эта зависимость от предыстории действует как память, которая, возможно, ответственна за память человека. Важно отметить, что веса синапсов могут изменяться со временем, а значит, меняется и поведение соответствующих нейронов.
Кора головного мозга человека содержит около 1011 нейронов и представляет собой протяженную поверхность толщиной от 2 до 3 мм с площадью около 



Нейроны взаимодействуют короткими сериями импульсов продолжительностью, как правило, несколько миллисекунд. Сообщение передается посредством частотно-импульсной модуляции. Частота может изменяться от нескольких единиц до сотен герц, что в миллион раз медленнее, чем быстродействующие переключательные электронные схемы Тем не менее сложные задачи распознавания человек решает за несколько сотен миллисекунд. Эти решения контролируются сетью нейронов, которые имеют скорость выполнения операций всего несколько миллисекунд. Это означает, что вычисления требуют не более 100 последовательных стадий. Другими словами, для таких сложных задач мозг «запускает» параллельные программы, содержащие около 100 шагов Рассуждая аналогичным образом, можно обнаружить, что количество информации, посылаемое от одного нейрона другому, должно быть очень малым (несколько бит). Отсюда следует, что основная информация не передается непосредственно, а захватывается и распределяется в связях между нейронами.
Оглавление
- Введение
- Часть I. ТЕОРИЯ
- 1.1. Биологический нейрон
- 1.2. Структура и свойства искусственного нейрона
- 1.3. Классификация нейронных сетей и их свойства
- 1.3.1. Теорема Колмогорова-Арнольда
- 1.3.2. Работа Хехт-Нильсена
- 1.3.3. Следствия из теоремы Колмогорова-Арнольда – Хехт-Нильсена
- 1.4. Постановка и возможные пути решения задачи обучения нейронных сетей
- 1.4.1. Обучение с учителем. Алгоритм обратного распространения ошибки
- 1.4.2. Обучение без учителя
- 1.5. Настройка числа нейронов в скрытых слоях многослойных нейронных сетей в процессе обучения
- 1.5.2. Конструктивные алгоритмы
- 1.6. Краткое обобщение материалов главы
- 1.6.2. Обучение нейронной сети
- 1.6.3. Применение обученной нейронной сети
- Глава 2. ОСНОВНЫЕ КОНЦЕПЦИИ НЕЙРОННЫХ СЕТЕЙ
- 2.1. Ассоциативная память нейронных сетей
- 2.2. Персептроны
- 2.3. Нейронные сети встречного распространения
- 2.4. Оптимизирующие нейронные сети
- 2.4.2. Нейронные сети Хэмминга
- 2.5. Двунаправленная ассоциативная память
- 2.6. Сети адаптивной резонансной теории
- 2.7. Когнитрон
- 2.8. Неокогнитрон
- 3.1. Нечеткая информация
- 3.1.2. Операции над нечеткими множествами
- 3.1.3. Нечеткие и лингвистические переменные
- 3.1.4. Нечеткие отношения
- 3.2. Нечеткий логический вывод
- 3.3. Эффективность нечетких систем принятия решений
- 3.4. Синтез нечетких нейронных сетей
- 3.4.2. Алгоритмы обучения и использования нечетких нейронных сетей
- 3.5. Нечеткий классификатор
- 3.6. Генетические алгоритмы
- 3.6.2. Что такое генетический алгоритм
- 3.6.3. Обучение нечетких нейронных сетей на основе генетических алгоритмов
- 3.6.4. Особенности генетических алгоритмов
- Часть II. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
- Глава 4. ОСНОВНЫЕ ФУНКЦИОНАЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММ МОДЕЛИРОВАНИЯ НЕЙРОННЫХ СЕТЕЙ
- 4.1. Общие сведения о программах моделирования нейронных сетей
- 4.2. Характеристики современных нейропакетов
- Глава 5. ПРОГРАММЫ МОДЕЛИРОВАНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 5.2. Нейропакет НейроПро (NeuroPro)
- 5.3. Нейропакет QwikNet32
- 5.4. Нейропакет Neural Planner
- 5.5. Нейропакет BrainMaker
- 5.6. Нейропакет MPIL
- 5.7. Нейропакет Braincel
- 5.8. Нейропакет Excel Neural Package
- 5.9. Пакет Fuzzy Logic Toolbox
- Часть III. ПРИМЕНЕНИЕ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- Глава 6. ПРИМЕРЫ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ
- 6.2. Анализ данных социологического опроса
- 6.3. Выявление показателей, влияющих на валовую прибыль предприятия
- 6.4. Задача об ирисах Фишера
- 6.5. Задача о землекопах
- 6.6. Аппроксимация функции
- 6.7. Нейросетевая экспертная система
- 6.8. Прогнозирование на финансовом рынке
- 6.9. Сжатие информации
- 6.10. Компактное представление информации репликативными нейронными сетями
- 6.11. Кратко о других задачах
- П.1. Основные парадигмы нейронных сетей
- П.2. Алгоритмы обучения нейронных сетей
- П.3. Глоссарий
- Список литературы

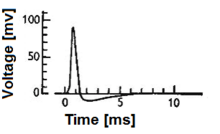
A модель биологического нейрона, также известная как модель нейрона с импульсами, представляет собой математическое описание свойств определенных клеток нервной системы, генерирующих резкие электрические потенциалы через их клеточную мембрану длительностью примерно одну миллисекунду, как показано на рис. 1. Пиковые импульсы нейронов известны как основная сигнальная единица нервной системы, и по этой причине характеристика их работы имеет большое значение. Стоит отметить, что не все клетки нервной системы производят спайк, который определяет область действия моделей спайк-нейронов. Например, улитковые волосковые клетки, рецепторные клетки сетчатки и биполярные клетки сетчатки не образуются. Кроме того, многие клетки нервной системы не классифицируются как нейроны, а вместо этого классифицируются как глия.

В конечном итоге, биологические модели нейронов на объяснение механизмов, лежащих в основе работы нервной системы контроля восстановления утраченных возможностей таких как восприятие (например, глухота или слепота), принятие решений и непрерывный контроль конечностей. В этом смысле модели биологических нейронов отличаются от моделей искусственных нейронов, которые не предполагают предсказывать результаты экспериментов с биологической нервной ткани (хотя модели искусственных нейронов также связаны с выполнением задач восприятия и оценки). Соответственно, важным аспектом биологических нейронов является экспериментальная проверка и использование физических объектов для описания экспериментальной процедуры.
Модели нейронов можно разделить на две категории в соответствии с физическими единицами интерфейса модели. Каждую модель можно использовать в соответствии с уровнем абстракции / детализации:
- Моделирование электрического входного-выходного напряжения мембраны — Эти модели позволяют прогнозировать выходное напряжение мембраны в зависимости от электростимуляции, заданное как входной ток или напряжение. Различные модели в этой категории отличаются точным функциональным устройством между входным током и выходным напряжением. Некоторые модели в этой категории являются моделями черного ящика и различают только два измеренных уровня напряжения: наличие всплеска (также известный как «потенциал») или состояние покоя. Другие модели более подробны и учитывают субклеточные процессы. Модели в этой категории могут быть детерминированными или вероятностными.
- Естественные или фармакологические модели входных нейронов этой категории связаны между входным стимулом, который может быть фармакологическим или естественным, и вероятность всплеска. Входящие каскад этих моделей не является электрическим, имеет либо фармакологические (химические) единицы, которые имеют другие физические единицы, которые имеют другие физические силы, такие как свет, звук формы физического давления. Кроме того, выходной каскад представляет вероятность возникновения всплеска, а не электрического напряжения.
Хотя в науке и технике нет ничего необычного в наличии нескольких описательных моделей для разных уровней абстракции / детализации, различных, иногда противоречие, биологических моделей нейронов исключительно высоки. Это частично является результатом различных различных экспериментальных ситуаций и сложных ситуаций одного и того же взаимодействия различных клеток (сетевые эффекты). Чтобы ускорить переход к единой теории, мы перечисляем несколько моделей в каждой категории и, где это возможно, также ссылки на поддерживающие эксперименты.
Содержание
- 1 Модели электрических входов-выходов с мембранным напряжением
- 1.1 Ходжкина — Хаксли
- 1.2 Perfect Integrate-and-fire
- 1.3 Leaky Integrate-and-Fire
- 1.4 Адаптивная интеграция- и -fire
- 1.5 Неплотный интегрируй-и-огонь дробного порядка
- 1,6 «Экспоненциальная интеграция и огонь» и «Адаптивная экспоненциальная интеграция и огонь»
- 1,7 Гальвес — Лёчербах
- 1,8 ФитцХью– Нагумо
- 1.9 Моррис — Лекар
- 1.10 Хиндмарш — Роуз
- 1.11 Тета-модель и квадратичная интеграция-и-огонь.
- 1.12 Теория кабеля
- 1.13 Компартментные модели
- 2 Модели нейронов естественного входного стимула
- 2.1 Неоднородная модель пуассоновского процесса (Зиберт)
- 2.2 Марковская модель с двумя состояниями (Носсенсон и Мессер)
- 2.3 Немарковские модели
- 3 Фармакологические модели нейронов входного стимула
- 3.1 Синаптические модели передачи (Кох и Сегев)
- 3.2 Модель Маркова с двумя состояниями (Носсенсон и Мессер)
- 4 Модель нейрона HTM
- 5 Применения
- 5.1 Электрический протез сетчатки
- 5.2 Протез сетчатки на основе нейротрансмиттера sis
- 5.3 Кохлеарный имплант
- 5.4 Интерфейс мозг-компьютер
- 5.4.1 Управление искусственными конечностями и ощущениями
- 6 Связь между искусственными и биологическими моделями нейронов
- 7 Предположения относительно роли нейрона в более широком контексте контекста работы
- 7.1 Схема обнаружения энергии на основе нейротрансмиттера
- 8 Общие комментарии относительно современных перспектив научных и и нженерных моделей
- 9 См. также
- 10 Ссылки
Электрический ввод –Модели выходного мембранного напряжения
этой
Модели в категории описывают взаимосвязь между мембранными токами нейронов на входном каскаде и мембранным напряжением на выходном каскаде. Наиболее широкое экспериментальное исследование этой категории было проведено Ходжкином-Хаксли в начале 1950-х годов с использованием экспериментальной установки, которая прокалывала клеточную мембрану и позволяет вызвать определенное напряжение / ток мембраны.
Самые современные электрические нейронные интерфейсы применяют внеклеточную электрическую стимуляцию, чтобы избежать прокола мембраны, что может привести к гибели клеток и повреждению тканей. Следовательно, неясно, в какой мощности электрические модели нейронов подходят для внеклеточной стимуляции (см., Например).
Ходжкина — Хаксли
| Свойство модели HH | Ссылки |
|---|---|
| Форма отдельного пика | |
| Идентичность участвующих других | |
| Пиковая скорость по аксону |
Модель Ходжкина — Хаксли (модель HH) — это взаимосвязь между потоком ионных токов через мембрану нейрональной клетки и мембранным напряжением клетки. Он состоит из набора нелинейных дифференциальных уравнений, описывающих поведение ионных каналов, пронизывающих клеточную мембрану гигантского аксона кальмара. За эту работу Ходжкин и Хаксли были удостоены Нобелевской премии 1963 года по физиологии и медицине.
Мы отмечаем взаимосвязь напряжение-ток с множественными зависимыми от напряжения токами, заряжающими клеточную мембрану емкостью C m
- C md V (t) dt = — ∑ i I i (t, V) { displaystyle C _ { mathrm {m}} { frac {dV (t)} {dt}} = — sum _ {i} I_ {i} (t, V)}
.
Приведенное выше уравнение — это время производная закона емкости, Q = CV, где изменение общего заряда должно быть объяснено как сумма по токам. Каждый ток задается законом Ома как
- I (t, V) = g (t, V) ⋅ (V — V eq) { displaystyle I (t, V) = g (t, V) cdot (VV _ { mathrm {eq}})}
где g (t, V) — это проводимость, или обратное сопротивление, которое можно разложить на постоянное среднее значение ḡ и совместную активацию и инактивации m и h, которые определяют, сколько может проходить через доступные мембранные каналы. Это расширение задается формулой
- g (t, V) = g ¯ ⋅ m (t, V) p ⋅ h (t, V) q { displaystyle g (t, V) = { bar {g}} cdot m (t, V) ^ {p} cdot h (t, V) ^ {q}}
и наши дроби следуют кинетике первого порядка
- dm (t, V) dt = m ∞ (В) — м (т, В) τ м (В) знак равно α м (В) ⋅ (1 — м) — β м (В) ⋅ м { Displaystyle { гидроразрыва {дм (т, V)} {dt} } = { frac {m _ { infty} (V) -m (t, V)} { tau _ { mathrm {m}} (V)}} = alpha _ { mathrm {m}} (V) cdot (1-m) — beta _ { mathrm {m}} (V) cdot m}
с аналогичной динамикой для h, где мы можем использовать либо τ, либо m ∞ или α и β, чтобы определить наши доли ворот.
Модель Ходжкина — Хаксли может быть расширена за счет включения дополнительных ионных токов. Обычно они включают входящие токи Ca и Na, а также несколько разновидностей выходных токов K, включая ток утечки.
Конечным результатом может быть около 20 параметров, которые необходимо оценить или измерить для получения точной модели. Для сложных систем нейронов интеграция соотношений требует больших вычислительных ресурсов. Поэтому необходимы тщательные упрощения модели Ходжкина — Хаксли.
Идеальная интеграция и запуск
Одна из самых ранних моделей нейрона — это идеальная модель интеграции и запуска, впервые исследованная в 1907 году Луи Лапик. Нейрон его представлен мембранным напряжением V, который вовлекается во время стимуляции входным током I (t) согласно
- I (t) = C d V (t) dt { displaystyle I (t) = C { frac {dV (t)} {dt}}}
, который является просто временной производной законом емкости, Q = CV. Когда подается входной ток, мембранное напряжение увеличивается со временем, пока не достигнет постоянного порогового значения V th, в этот момент возникает всплеск дельта-функции, и напряжение сбрасывается до состояния покоя. потенциал, после чего модель продолжает работать. Таким образом, частота срабатывания модели неограниченно линейно увеличенный класс входного тока.
Модель можно сделать более точной, введя рефрактерный период t ref, который ограничивает частоту срабатывания нейрона, предотвращая его срабатывание в течение этого периода. Для постоянного входа I (t) = I пороговое напряжение достигается по истечении времени интегрирования t int = CV thr / I после старта с нуля. После сброса рефрактерный период вводит мертвое время, так что общее время до следующего срабатывания равно t ref + t int. Частота срабатывания обратна полному интервалу между импульсами (включая мертвое время). Таким образом, частота срабатывания как функция постоянного входного тока равна
- f (I) = ICV th + tref I { displaystyle , ! F (I) = { frac {I} {C _ { mathrm {}} V _ { mathrm {th}} + t _ { mathrm {ref}} I}}}
.
Недостатком этой модели является то, что она не входит ни адаптации, ни утечки. Заработок в области ускорения. Эта характеристика явно не соответствует наблюдаемому поведению нейронов. Следующие расширения делают модель интеграции и стрельбы более правдоподобной биологической точки зрения.
Негерметичная интеграция и возгорание
Модель протекающей интеграции и возгорания, восходящая к Луи Лапику, по сравнению с негерметичной интеграцией, содержит смоделировать член «утечки» в уравнении мембранный, отражающий диффузию через мембрану. Уравнение модели выглядит так (модель с утечкой интегрирования и возгорания, глава 4,1 дюйма)
- C md V m (t) dt = I (t) — V m (t) R m { displaystyle С _ { mathrm {m}} { frac {dV _ { mathrm {m}} (t)} {dt}} = I (t) — { frac {V _ { mathrm {m}} (t)} {R _ { mathrm {m}}}}}
где V m — напряжение на клеточной мембране, а R m — сопротивление мембраны. (Модель интегрирования и возгорания без утечки восстанавливается в пределе R m до бесконечности, т.е. если мембрана является идеальным изолятором). Уравнение модели действительно для произвольного зависящего от времени входа, пока не достигнуто пороговое значение V th ; после этого мембранный потенциал сбрасывается.
Для постоянного входа минимальный вход для достижения равенства I th = V th / R m. Предполагаемая сброс на ноль, частота срабатывания выглядит как
- f (I) = {0, I ≤ I th [tref — R m C m log (1 — V th IR m)] — 1, I>I th { displaystyle f (I) = { begin {case} 0, I leq I _ { mathrm {th}} \ {[} t _ { mathrm {ref}} -R _ { mathrm {m }} C _ { mathrm {m}} log (1 — { tfrac {V _ { mathrm {th}}} {IR _ { mathrm {m}}}}) {]} ^ {- 1 }, I>I _ { mathrm {th}} end {ases}}
который сходится для больших входных токов к предыдущей модели безрактерчек с периодом. также может быть распространено на тормозящие нейроны.
Самый большой недостаток Дырявого нейрона интеграции и запуска заключается в том, что он не содержит нейронной адаптации, поэтому он может описать экспериментально измеренную последовательность импульсов в ответ на постоянный входной то к. Этот недостаток устранен в обобщенной версии «Интегрируй и стреляй». модели, которые также вводят переменную адаптацию с высокой степенью точности предсказывать время спайков корковых нейронов при токе.
Адаптивная интеграция и запуск
Нейрональная адаптация относится к Дело в том, что даже при наличии постоянной подачи тока в некоторые интервалы между выбросами на выходе увеличиваются. Адаптивная модель нейрона интеграции и активации сочетает интеграцию напряжения V с одними или адаптационными переменными w k (см. главу 6.1 в учебнике Neuronal Динамика)
τ мд В м (т) dt знак равно RI (т) — [В м (т) — Е м] — R ∑ kwk { displaystyle tau _ { mathrm {m}} { frac {dV _ { mathrm {m}} (t)} {dt}} = RI (t) — [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] — R sum _ {k} w_ {k}}
τ kdwk (t) dt = — ak [V m (t) — E m] — wk + bk τ k ∑ е δ (t — tf) { displaystyle tau _ {k} { frac {dw_ {k} (t)} {dt}} = — a_ {k} [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] — w_ {k } + b_ {k} tau _ {k} sum _ {f} delta (tt ^ {f})}
где τ m { displaystyle tau _ {m}}

Интегрируйте и запускайте нейроны с одной или несколькими переменными адаптациями, которые включают множество возбудителей нейронов в ответ на постоянную стимуляцию, включая адаптацию, взрыв и начальный взрыв. Более того, адаптивные нейроны с интеграцией и запуском с использованием адаптационных переменными предсказывать время всплесков корковых нейронов при зависящей от времени инъекции тока в сому.
Неплотный интегрируй-и-стреляй дробного порядка
Недавние достижения в области вычислительного и теоретического дробного исчисления привели к новой форме модели, получившей название «интегрировать и запустить с утечкой дробного порядка». «Преимущество этой модели» состоит в том, что она может использовать эффекты адаптации с помощью одной новой модели. Модель имеет следующий вид
- I (t) — V m (t) R m = C md α V m (t) d α t { displaystyle I (t) — { frac {V _ { mathrm {m }} (t)} {R _ { mathrm {m}}}} = C _ { mathrm {m}} { frac {d ^ { alpha} V _ { mathrm {m}} (t) } {d ^ { alpha} t}}}
Как только напряжение достигает порогового значения, оно сбрасывается. Для учета адаптации нейронов в экспериментальных данных использовалась дробная интеграция.
«Экспоненциальная интеграция и запуск» и «Адаптивная экспоненциальная интеграция и запуск»
В экспоненциальной интегрировать и активировать модель, генерация всплесков экспоненциальна в соответствии с уравнением:
- d В dt — р τ м я (t) знак равно 1 τ м [Е м — V + Δ T ехр (V — VT Δ T)] { displaystyle { frac {dV} {dt}} — { frac {R} { tau _ {m}}} I (t) = { frac {1} { tau _ {m}}} [E_ {m} -V + Delta _ {T} exp left ({ frac {V-V_ {T}} { Delta _ {T}}} right)]}
.
где V { displaystyle V}






В адаптивном экспоненциальном нейроне интегрирования и включения указанная выше экспоненциальная нелинейность уравнения напряжения комбинируется с переменной адаптации w
τ md V dt = RI (t) + [E m — V + Δ T exp (V — VT Δ T)] — R w { displaystyle tau _ {m} { frac {dV} {dt}} = RI (t) + [E_ {m } -V + Delta _ {T} exp left ({ frac {V-V_ {T}} { Delta _ {T}}} right)] — Rw}
τ dw (t) dt Знак равно — a [В м (T) — E м] — вес + б τ δ (t — tf) { displaystyle tau { frac {dw (t)} {dt}} = — a [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] — w + b tau delta (tt ^ {f})}
где w обозначает ток адаптации во времени масштаб τ { displaystyle tau}



Гальвес-Лёчербах

Модель Гальвса — Лёчербаха представляет собой конкретное развитие дырявая модель интеграции и возгорания. Это по своей сути стохастический. Его разработали математики Антонио Гальвес и. С учетом указанной модели, вероятность того, что данный нейрон i { displaystyle i}

P rob (X t (i) = 1 | F t — 1) = ϕ i (∑ j ∈ IW j → i ∑ s = L tit — 1 gj (t — s) X s (j), τ — L ti), { displaystyle mathop { mathrm {Prob}} (X_ {t} (i) = 1 | { mathcal {F}} _ {t-1}) = phi _ {i} { Biggl (} sum _ {j in I} W_ {j rightarrow i} sum _ {s = L_ {t} ^ {i}} ^ {t-1} g_ {j} (ts) X_ { s} (j), ~~~ t-L_ {t} ^ {i} { Biggl)},}
где W j → i { displaystyle W_ {j rightarrow i}}






L ti = sup {s < t : X s ( i) = 1 }. {displaystyle L_{t}^{i}={text{sup}}{s
ФитцХью — Нагумо
Шве Упрощения эпинга для Ходжкина-Хаксли были введены ФитцХью и Нагумо в 1961 и 1962 годах. Стремясь описать «регенеративное самовозбуждение» с помощью нелинейного мембранного напряжения с положительной обратной связью и восстановления с помощью линейного напряжения затвора с отрицательной обратной связью, они разработали описанную модель на
- d V dt = V — V 3/3 — w + I ext τ dwdt = V — a — bw { displaystyle { begin {array} {rcl} { dfrac {dV} {dt}} = VV ^ {3} / 3-w + I _ { mathrm {ext }} \ tau { dfrac {dw} {dt}} = Va-bw end {array}}
, где мы снова имеем мембранное напряжение и входной ток с более медленным общим напряжением затвора w и экспериментально определенными значениями a = -0,7, b = 0,8, τ = 1 / 0,08. Эта модель явно не выводится из биологии. Экспериментальная поддержка слабая.
Моррис-Лекар
В 1981 году Моррис и Лекар объединили модели Ходжкина-Хаксли и ФитцХью-Нагумо в модели потенциалаозависимого кальциевого канала с калиевым каналом с задержанным выпрямителем, представленным
- C d V dt Знак равно — I ion (V, w) + I dwdt = ϕ ⋅ вес ∞ — вес τ w { displaystyle { begin {array} {rcl} C { dfrac {dV} {dt}} = — I _ { mathrm {ion}} (V, w) + I \ { dfrac {dw} {dt}} = phi cdot { dfrac {w _ { infty} -w} { tau _ {w}}} end {array}}}
где I ion (V, w) = g ¯ C am ∞ ⋅ (V — VC a) + g ¯ K w ⋅ (V — VK) + г ¯ L ⋅ (V — VL) { displaystyle I _ { mathrm {ion}} (V, w) = { bar {g}} _ { mathrm {Ca}} m _ { infty} cdot (VV _ { mathrm {Ca}}) + { bar {g}} _ { mathrm {K}} w cdot (VV _ { mathrm {K}}) + { bar {g}} _ { mathrm {L}} cdot (VV _ { mathrm {L}})}
Хиндмарш — Роуз
Основываясь на модели ФитцХью — Нагумо, Хиндмарш и Роузили в 1984 году модель нейронной активности описывалась тремя связанными дифференциа льными уравнениями первого порядка:
- dxdt = y + 3 x 2 — x 3 — z + I dydt = 1–5 x 2 — ydzdt = r ⋅ (4 (x + 8 5) — z) { displaystyle { begin {array} {rcl} { dfrac {dx} {dt}} = y + 3x ^ {2} -x ^ {3} -z + I \ { dfrac {dy} {dt}} = 1-5x ^ {2} -y \ { dfrac {dz} {dt}} = r cdot (4 (x + { tfrac {8} {5}}) — z) end {array}}}
с r = x + y + z и r ≈ 10, так что переменная z только меняется очень медленно. Эта дополнительная математическая допускает большое разнообразие динамических характеристик мембранного, описываемого типа x модели, включая хаотическую динамику. Это делает модель нейрона Хиндмарша — Роуза очень полезной, поскольку качественно все еще простой, позволяет описать множество различных паттернов действия, наблюдаемых в экспериментах.
Тета-модель и квадратичная интеграция-и-огонь.
тета-модель, или каноническая модель Эрментроута — Копелла, математически эквивалентна квадратичной модели интегрирования и включения, которая, в свою очередь, является приближением к экспоненциальной модель интеграции и стрельбы и модель Ходжкина-Хаксли. Это называется канонической моделью, потому что это одна из общих моделей для постоянного входа, близкого к точке бифуркации, что означает близость перехода от бесшумного к повторяющемуся срабатыванию.
Уравнение для квадратичного интегрирования-и- Модель пожара (см. главу 5.3 в учебнике «Нейронная динамика»)
τ md V m (t) dt = (I — I 0) R + [В м (т) — Е м] [В м (т) — VT] { displaystyle tau _ { mathrm {m}} { frac {dV _ { mathrm {m}} (т)} {dt}} = (I-I_ {0}) R + [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] [V _ { mathrm {m} } (t) -V _ { mathrm {T}}]}
Эквивалентность тета-модели и квадратичной интеграции-и-зажигания, например, рассматривается в главе 4.1.2.2 Spiking Neuron Models.
Для входа I (t), который изменен со временем или вдали от точки бифуркации, предпочтительнее работать с экспоненциальной моделью интегрировать и запустить (если кто-то хочет остаться в классе одномерных моделей нейронов), потому что реальные нейроны демонстрируют нелинейность эксцентриситета. Поненциальная модель интегрирования и возгорания.
Теория кабеля
Теория кабеля дендритную ветвь как цилиндрическую стойкую, подвергающуюся регулярному шаблону бифуркации, как ветви на дереве. Для одного цилиндра или всего дерева входная проводимость в основании (где дерево встречается с телом ячейками или любой такой границей) как определяется как
- G in = G ∞ tanh (L) + GL 1 + (GL / G ∞) tanh ( L) { displaystyle G_ {in} = { frac {G _ { infty} tanh (L) + G_ {L}} {1+ (G_ {L} / G _ { infty}) tanh ( L)}}}
,
где L — электротоническая длина цилиндра, которая зависит от его длины, диаметра и сопротивления. Простой рекурсивный алгоритм линейно переводится с ветвей и другая программа для эффективной проводимости дерева. Это задается как
- GD = G m AD tanh (LD) / LD { displaystyle , ! G_ {D} = G_ {m} A_ {D} tanh (L_ {D}) / L_ {D}}
где A D = πld — общая площадь поверхности дерева общей длиной l, а L D — его полная электротонная длина. Для всегорона, в котором проводимость нейрона клетки составляет G S, проводимость мембраны на единицу площади равна G md = G m / A, мы на общую проводимость нейрона G N для n дендритных деревьев путем сложения проводимости всех деревьев и сомы, полученной как
- GN = GS + ∑ j = 1 n AD j F dgaj { displaystyle G_ {N} = G_ {S } + sum _ {j = 1} ^ {n} A_ {D_ {j}} F_ {dga_ {j}}}
,
где мы можем найти общий поправочный коэффициент F dga экспериментально, отмечая G D = G mdADFdga.
Компартментные модели
Модель кабеля делает ряд упрощений для получения закрытых аналитических результатов, а именно, что дендритная ветвь должна разветвляться в убывающих парах по фиксированной схеме. Компартментная модель допускает любую желаемую топологию с произвольными ветвями и длинами, но упрощает взаимодействие между ветвями для компенсации. Таким образом, две модели дают дополнительные результаты.
Каждая отдельная часть или дендрита моделируется прямым цилиндром произвольной длины l и диаметром d, который соединяется с фиксированным сопротивлением с любым разветвленным цилиндров. Определим коэффициент проводимости i-го цилиндра как B i = G i / G ∞, где G ∞ = π d 3/2 2 Р я р м { displaystyle G _ { infty} = { tfrac { pi d ^ {3/2}} {2 { sqrt {R_ {i} R_ {m}}}}}}
- B out, я знак равно B in, я + 1 (di + 1 / di) 3/2 R m, i + 1 / R m, i { displaystyle B _ { mathrm {out}, i} = { frac {B _ { mathrm {in}, i + 1} (d_ {i + 1} / d_ {i}) ^ {3/2}} { sqrt {R _ { mathrm {m}, i + 1} / R_ { mathrm {m}, i}}}}}
- B in, i = B out, i + tanh X i 1 + B out, я tanh X i { displaystyle B _ { mathrm {in}, i} = { frac {B _ { mathrm {out}, i} + tanh X_ {i}} {1 + B _ { mathrm {out}, i} tanh X_ {i}}}}
- B out, par = B in, dau 1 (ddau 1 / dpar) 3/2 R m, dau 1 / R m, par + B in, dau 2 (ddau 2 / dpar) 3/2 R m, dau 2 / R m, par +… { displaystyle B _ { mathrm {out, par}} = { frac {B _ { mathrm {in, dau1}} (d _ { mathrm {dau1}} / d _ { mathrm {par}}) ^ {3/2}} { sqrt {R _ { mathrm {m, dau1}} / R _ { mathrm {m, par}}}}} + { гидроразрыв {B _ { mathrm {in, dau2}} (d _ { mathrm {dau 2}} / d _ { mathrm {par}}) ^ {3/2}} { sqrt {R _ { mathrm {m, dau2}} / R _ { mathrm {m, par}}}} } + ldots}
где последнее уравнение относится к родителям и дочерям в филиалах, а X i = li 4 R idi R m { displaystyle X_ {i} = { tfrac {l_ {i} { sqrt {4R_ {i}}}}} { sqrt {d_ {i} R_ {m}}}}}
- GN = A soma R m, soma + ∑ j B in, stem, j G ∞, j { displaystyle G_ {N} = { frac {A _ { mathrm {soma }}} {R _ { mathrm {m, soma}}}} + sum _ {j} B _ { mathrm {in, stem}, j} G _ { infty, j}}
.
Пример Компартментную модель нейрона с алгоритмом уменьшения количества отсеков (увеличения скорости вычислений) и при этом основных показателей можно найти в.
Модели нейронов естественного входного стимула
Модели этой категории были созданы в результате экспериментов с естественной стимуляцией, такие как свет, звук, прикосновение или запах. В этих условиях экспериментов характер спайков, стимулирует результаты испытаний к испытанию, но усредненный ответ от нескольких испытаний часто сходится к четкому образцу. Следовательно, модели этой категории генерируют вероятностную взаимосвязь между входным стимулом и возникновением всплесков.
Неоднородная модель пуассоновского процесса (Зиберт)
Зиберт смоделировалтерн возбуждения спайков нейрона, используя не- однородную модель пуассоновского процесса, следующие эксперименты со слуховой система. Согласно Зиберту, вероятность всплеска в интервале времени [t, t + Δ t] { displaystyle [t, t + Delta _ {t}]}![{ displaystyle [t, t + Delta _ {t}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a5f74c8e9f1b771d10e66322f05d9692676551b)
![{ displaystyle g [s (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f02d6c931d32be9a417598bb7164a38b18e7c7)

П спайк (t ∈ [t ′, t ′ + Δ t]) = Δ t ⋅ g [s (t)] { displaystyle P_ {spike} (t in [t ‘, t’ + Delta _ { t}]) = Delta _ {t} cdot g [s (t)]}
Сиберт рассматривал несколько функций как g [s (t)] { displaystyle g [s (t)]}![{ displaystyle g [s (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79f02d6c931d32be9a417598bb7164a38b18e7c7)
![{ displaystyle г [s (t)] propto s ^ {2} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/279ad33854b65b37667308913d562014bdb7f30a)
Основное преимущество модели Зиберта — ее простота. Недостатком модели является ее неспособность должным образом отразить следующие явления:
- свойство нейрона подчеркивать края в ответ на импульс стимула.
- насыщение скорости возбуждения.
- Значения межпикового интервала- гистограммы при значениях коротких интервалов (близких к нулю).
Эти недостатки устранены моделью Маркова с двумя состояниями.
Два состояния Модель Маркова (Носсенсон и Мессер)
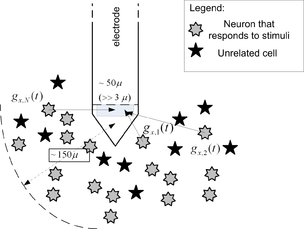
Модель пикового нейрона, разработанная Носсенсоном и Мессером, вырабатывает вероятность того, что нейрон вызовет спайк в зависимости от внешнего или фармакологического стимула. Модель состоит из каскада модели рецепторного слоя и модели нейрона с импульсами, как показано на рис. 4. Связь между внешним стимулом и вероятностью выброса осуществляется в два этапа: во-первых, модель рецепторной клетки преобразует исходный внешний стимул. с концентрацией нейротрансмиттера, то модель пикового нейрона связывает концентрацию нейротрансмиттера с частотой срабатывания (вероятность пика). Таким образом, модель импульсного нейрона сама по себе зависит от концентрации нейротрансмиттера на входной стадии.


Важной особенностью этой модели является прогнозирование модели частоты срабатывания нейронов, которая фиксирует, используя небольшое количество свободных параметров, характерную реакцию с подчеркнутым краем нейронов к импульсу стимула, как показано на рис. 5. Скорость возбуждения определяется как нормализованная вероятность возбуждения нервного импульса, так и величина, пропорциональная току нейротрансмиттеров, высвобождаемых клеткой. Выражение для скорости стрельбы имеет следующий вид:
R fire (t) = P spike (t; Δ t) Δ t = [y (t) + R 0] ⋅ P 0 (t) { displaystyle R_ {огонь} (t) = { frac {P_ {spike} (t; Delta _ {t})} { Delta _ {t}}} = [y (t) + R_ {0}] cdot P_ {0} (t)}
где,
- P0 — вероятность того, что нейрон будет «активирован» и готов к срабатыванию. Он задается следующим дифференциальным уравнением:
P ˙ 0 = — [y (t) + R 0 + R 1] ⋅ P 0 (t) + R 1 { displaystyle { dot {P}} _ { 0} = — [y (t) + R_ {0} + R_ {1}] cdot P_ {0} (t) + R_ {1}}
P0 обычно можно вычислить рекурсивно с использованием метода Эйлера, но в в случае импульса стимула это дает простое выражение в замкнутой форме.
- y (t) является входом модели и интерпретируется как концентрация нейромедиатора в окружающей клетке (в большинстве случаев глутамат). Для внешнего стимула его можно оценить с помощью модели рецепторного слоя:
y (t) ≃ ggain ⋅ ⟨s 2 (t)⟩ { displaystyle y (t) simeq g_ {gain} cdot langle s ^ {2} (t) rangle}

- R0 соответствует внутренней скорости спонтанного возбуждения нейрона.
- R1 — скорость восстановления нейрона из рефрактерного состояния.
Другие прогнозы этой модели включают:
1) Усредненный потенциал вызванного ответа (ERP), обусловленный популяцией множества нейронов в нефильтрованных измерениях, похож на частоту возбуждения.
2) Изменение напряжения активности из-за активности нескольких нейронов напоминает частоту возбуждения (также известную как мощность нескольких активностей или MUA).
3) Распределение вероятностей между интервалами всплесков принимает форму функции, подобной гамма-распределению.
| Свойство модели Носсенсон и Мессер | Ссылки | Описание экспериментальных данных |
|---|---|---|
| Форма скорости стрельбы в ответ на импульс слухового стимула | Скорость стрельбы имеет та же форма, что и на рис. 5. | |
| Форма скорости стрельбы в ответ на импульс визуального стимула | Скорость стрельбы имеет ту же форму, что и на рис. 5. | |
| Форма скорости стрельбы в ответ на импульс обонятельного стимула | Скорость стрельбы такая же, как на рис. 5. | |
| Форма скорости стрельбы в ответ на сомато-сенсорный стимул | Скорость возбуждения имеет ту же форму, что и на рис. 5. | |
| Изменение скорости возбуждения в ответ на применение нейромедиатора (в основном глутамата) | Изменение скорости возбуждения в ответ на приложение нейротрансмиттера (Glutamat e) | |
| Квадратная зависимость между давлением слухового стимула и скоростью возбуждения. | Квадратная зависимость между давлением слухового стимула и скоростью возбуждения (- Линейная зависимость в квадрате давления (мощности)). | |
| Квадратная зависимость между электрическим полем визуального стимула (вольты) и интенсивностью возбуждения | Квадратная зависимость между электрическим полем визуального стимула (вольт) — линейная зависимость между визуального стимула и скоростью развития. | |
| Форма статистики межпикового интервала (ISI) | Форма ISI похожа на гамма-функцию | |
| ERP похожа на частоту срабатывания в нефильтрованных измерениях | Форма усредненной вызванной способности в ответ на стимул напоминает темп стрельбы (рис. 5).). | |
| Мощность MUA похожа на частоту возбуждения | Форма эмпирической дисперсии внеклеточных импульсов в ответ на импульс стимула частоту возбуждения (рис. 5). |
Немарковские модели
Ниже представлен список опубликованных немарковских моделей нейронов:
- Джонсон и Свами
- Берри и Мейстер
- Касс и Вентура
Моделирование нейронов с фармакологическим входным стимулом
Модели этой категории позволяют делать прогнозы для экспериментов с фармакологической стимуляцией.
Синаптическая передача (Кох и Сегев)
Согласно модели Коха и Сегева, ответ нейрона на отдельные нейротрансмиттеры можно смоделировать как расширение классической модели Ходжкина-Хаксли с как стандартные, так и нестандартные кинетические токи. Четыре нейротрансмиттера в первую очередь на ЦНС. АМРА / каинатные рецепторы являются быстрыми возбуждающими медиаторами, тогда как рецепторы NMDA опосредуют значительно более медленные токи. Быстрые тормозящие токи проходят через ГАМК A рецепторы, а ГАМК B рецепторы опосредуются вторичным G-белком — активированные калиевые каналы. Этот диапазон посредничества дает следующую текущую динамику:
где ḡ — максимальная проводимость (около 1 S ), а E — равновесный потенциал данного иона или передатчика (AMDA, NMDA, Cl или K ), а [O] принадлежность открытых рецепторов. Для NMDA существует значительный эффект магниевого блока, который сигмоидально зависит от внутриклеточного магния посредством B (V). Для GABA B, [G] представляет собой концентрацию G-белка, а K d представляет собой диссоциацию G при связывании с воротами калия.
Динамика этой сложной модели была хорошо изучена экспериментально и дает важные результаты с точки зрения очень быстрого синаптического потенцирования и депрессии, то есть быстрого, краткосрочного обучения.
Модель Маркова с двумя состояниями (Носсенсон и Мессер)
Модель Носсенсона и Мессера переводит концентрацию нейротрансмиттера на входной стадии в вероятность высвобождения нейротрансмиттера на выходной стадии. Более подробное описание этой модели см. В разделе Марковская модель с двумя состояниями выше.
Модель нейрона HTM
Модель нейрона HTM была заблокирована Джеффом Хокинсом и исследователями из Numenta и основа теории под названием Иерархическая временная память, описанная в книге Об интеллекте. Он основан на неврологии, а также на физиологии и взаимодействии пирамидных нейронов в неокортексе человеческого мозга..
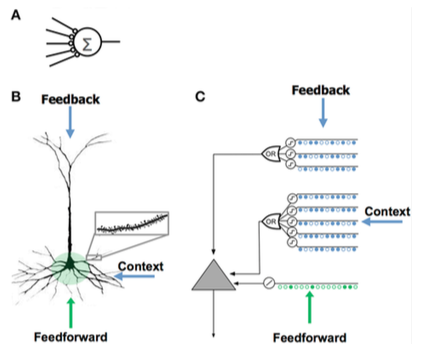
| Искусственная нейронная сеть (ANN) | Неокортикальный пирамидный нейрон (биологический Нейрон) | Нейрон модели HTM |
| — Мало синапсов
— Нет дендритов — Сумма входных x весов — Обучается путем изменения весов синапсов |
— Тысячи синапсы на дендритах
— Активные дендриты: клетка распознает уникальных паттернов — Совместная активация набора синапсов на дендритном сегменте вызывает спайк NMDA и деполяризацию в соме — Источники входных данных в клетку:
— учится путем выращивания новых синапсов |
— вдохновляется пирамидными клетками в слоях неокортекса 2/3 и 5
— Тысячи синапсов — Активные дендриты: клетка распознает уникальных паттернов — Моделирует дендриты и пики NMDA с каждым массивом совпадающих детекторов, имеющим набор синапсов — Обучение моделированию роста новых синапсов |
Приложения
Вопрос нейронного моделирования лежит в основе следующих проектов:
Электрический протез сетчатки
Дополнительная литература по этой теме:
нейротрансмиттер протез сетчатки
Дополнительная литература по этой теме:
Кохлеарный имплант
Интерфейс мозг-компьютер
Контроль и ощущения искусственных конечностей
Дополнительная литература по этой теме:
Связь между искусственными и биологическими моделями нейронов
Самая основная модель нейрона из входящего с некоторым вектором синаптического веса и функции активации или передаточной функции внутри выходного сигнала, определяющего нейрон. Это основная структура, используемая для искусственных нейронов, которая в нейронной сети часто выглядит как
yi = ϕ (∑ jwijxj) { displaystyle y_ {i} = phi left ( sum _ {j } w_ {ij} x_ {j} right)}
где y i — выход i-го нейрона, x j — сигнал j-го входного нейрона, w ij — синаптический вес (или сила связи) между нейронами i и j, а φ — функция активации. Хотя эта модель успешно используется в приложениях для машинного обучения, она не подходит для реальных (биологических) нейронов, поскольку в ней отсутствует зависимость от времени, демонстрируют спайки реальных нейронов. Именно такую форму принимают биологические модели типа «объединяй и огонь»; в и фармакологической литературе медицинской степени заменены кинетическими моделями, такими как модель Ходжки — Хаксли.
В случае моделирования биологического нейрона вместо абстракций, таких как «вес» и «», используются физические аналоги. Возбуждение нейрона включает движение в клетку, функцию передачи «. Нейрон заполнен и окружен водой, содержащей ионы, несущие электрические заряды. Нейрон из совместимой клеточной мембраной и может поддерживать заряженных других сторон, которая определяет емкость Cm. Это происходит, когда нейротрансмиттеры вызывают открытие ионных каналов на клеточной мембране. Мы описываем это физическим зависящим от времени током I (t).>напряжение или разности электрической мощности между окружающей средой, что иногда приводит к скачку напряжения , называемому потенциалом действия, проходит по длине клетки и запускает высвобождение дополнительных нейротрансмиттеров Таким образом, напряжение является величиной, представляющей интерес, и определяется как V m (t).
Предположения относительно роли нейрона в более широком контенте ексте принципа работы мозга
Схема обнаружения энергии на основе нейротрансмиттеров
Схема обнаружения энергии на основе нейротрансмиттеров предполагает, что нервная ткань химически функционирует обнаружение, подобную радиолокационную.

Как показано на рис. 6, основная идея гипотезы состоит в том, чтобы учитывать концентрацию нейротрансмиттера, генерацию нейротрансмиттера и скорость удаления нейротрансмиттера как важные величины при выполнении задачи обнаружения., относящимся к измеренным электрическим параметрам как к побочному эффекту, который только определенным условиям совпадает с функциональным назначением каждого шага. Схема включения на радароподобное «обнаружение энергии», потому что она включает в себя возведение сигнала в квадрат, временное суммирование и механизм переключения порогов, как и детектор энергии, но также включает блок, который выделяет стимулы стимула и переменную длину (переменная память). Согласно этой гипотезе, физиологическим эквивалентом статистики энергетического теста является нейротрансмиттера, а скорость возбуждения соответствует току нейротрансмиттера. Эта интерпретация состоит в том, что она приводит к единому последовательному объяснению, позволяет проводить электрофизиологические измерения, биохимические измерения и психофизические результаты.
Доказательства, рассмотренные в предположении следующая связь между функциональностью и гистологической классификацией:
- Возведение в квадрат стимула, вероятно, выполнено рецепторными клетками.
- Подчеркивание краев стимула и передача сигнала осуществляется нейронами.
- Накопление нейромедиаторов во времени осуществляется глиальными клетками. Кратковременное накопление нейротрансмиттеров также может происходить в некоторых типах нейронов.
- Логическое переключение осуществляется глиальными клетками, и оно является результатом превышения порогового уровня нейромедиатора. Это превышение порога также сопровождается изменением скорости утечки нейромедиаторов.
- Физическое переключение движения «все или без него» происходит из-за мышечных клеток и является результатом превышения определенного порога нейромедиаторов в окружении мышц.
Примечание. что, хотя электрофизиологические сигналы на рисунке 6 часто похожи на функциональный сигнал (мощность сигнала / уровень нейромедиатора / мышечная сила), есть некоторые этапы, на которых электрическое наблюдение отличается от функционального назначения соответствующего этапа. В частности, Носсенсон и др. предположили, что пересечение порога глии имеет совершенно другое функциональное действие по с излучаемым электрофизиологическим сигналом, и что последнее может быть только побочным эффектом разрыва глии.
Общие комментарии относительно современных научных и инженерных моделей
- Приведенные выше модели все еще являются идеализацией. Необходимо внести поправки на увеличенную площадь поверхности мембраны, обусловленную многочисленными дендритными шипами, значительно более высокими, чем экспериментальные данные при комнатной температуре, и неоднородностью внутренней структуры клетки. Некоторые наблюдаемые эффекты не укладываются в некоторых из этих моделей. Например, циклическое изменение температуры (с минимальным повышением чистой температуры) клеточной мембраны во время использования функции несовместимо с моделями, которые используют моделирование мембраны как сопротивление, которое должно рассеивать энергию, когда через нее протекает ток. Переходное утолщение клеточной мембраны во время использования также предсказывается этими моделями, как и изменение в результате этого утолщения, не включены в эти модели. Действие некоторых анестетиков, таких как инертные газы, также проблематично для этих моделей. Новые модели, такие как солитонная модель, пытаются объяснить эти явления, но они менее развиты, чем старые модели, и еще не получили широкого применения.
- Современные взгляды на роль науки модель предполагает, что «все модели ошибочны, но некоторые полезны» (Box and Draper, 1987; Gribbin, 2009; Paninski et al., 2009).
- Недавнее предположение предполагает, что каждый нейрон может функционировать как независимые пороговые устройства. Предполагается, что нейрон может быть анизотропно активирован по происхождению сигналов, поступающих к мембране, через его дендритные деревья. Было предложено, чтобы импульсная форма волны зависела от источника стимула.
См. Также
- Связывающий нейрон
- Байесовские подходы к функциям мозга
- Принцип свободной энергии
- Модели нейронных вычислений
- Нейронное кодирование
- Нейронные колебания
- Количественные модели потенциала действия
Ссылки
Аксон – это волокнистая ось, отходящая от тела нейрона, покрытая миелиновым слоем, обеспечивающая связь с другими нейронами и клетками рабочих органов. Представляет собой удлиненный осевой отросток, по которому передаются потенциалы действия (возбуждения), что делает его важнейшим структурным элементом ЦНС.
Определение
Мозговое вещество – высокоорганизованная структура, образованная нервными клетками, от которых отходят аксоны. Из нервных клеток состоит мозговая ткань. Аксон в переводе с греческого означает «ось» – это такой отросток, элемент мозгового вещества, который обеспечивает взаимодействие между клетками разного типа (нейроны, клетки иннервируемых органов), что ассоциируется с тонким, четким управлением работой органов и систем. Функции ткани ЦНС:
- Воспринимает раздражения, преобразуя их в импульсы.
- Поддерживает передачу импульсов от управляющих отделов мозга к исполнительным органам.
- Формирует ответную реакцию на раздражающее воздействие.
- Обеспечивает взаимодействие в работе систем и органов, поддерживает интеграцию структурных единиц организма.
- Обеспечивает взаимосвязь организма с внешней средой.
Согласно определению в биологии, аксон (англ. axon) – удлиненный отросток, по которому идут импульсы от тела нейрона к другим нервным клеткам и структурным элементам всех тканей организма. Мозговая ткань в период внутриутробного развития образуется из нервной пластины. Края пластинки прогибаются, что приводит к формированию валиков и желобка. В результате смыкания краев валиков возникает нервная трубка – основа ЦНС.
Дифференциация клеток, образующих трубку, приводит к появлению нейробластов и спонгиобластов. Первые служат основой для формирования нейронов, вторые – для образования нейроглии. Нейроны (анат.) – основные структурные элементы мозгового вещества. Они характеризуются отсутствием функции деления, что приводит к постепенному уменьшению их численности. Тело нейрона состоит из ядра и цитоплазмы. В зависимости от типа нейронов меняется геометрическая форма тела, которая бывает круглая, овальная, пирамидальная и другая.
Цитоскелет, состоящий из микротрубочек и нейрофибриллов, обеспечивает опорную и трофическую функцию. Цитоскелет поддерживает форму нейрона, обеспечивает транспорт веществ и органелл. От тела ответвляются отростки – единичный аксон и множественные дендриты. Аксон нейрона почти не ветвится, иногда образует коллатеральные (обходные) сегменты. Концевые сегменты (окончания) разветвляются, называются терминали.
Терминали взаимосвязаны с окончаниями других нейронов и с клетками, образующими паренхиму (ткань) рабочих органов – мышц, желез. Количество дендритов варьируется от 1 до нескольких. Тонкие ответвления дендритов оканчиваются небольшими шипами, где сосредоточены терминали аксональных отростков многих тысяч других клеток. Дендриты воспринимают раздражения или потенциалы действия от других клеток и передают их по волокнам к телу своего нейрона.
Рост аксона зависит от особенностей строения и жизнедеятельности нейрона, который поддерживает функцию питания отростка. К примеру, если перерезать аксональный ствол, сегмент, связанный с телом, остается жизнеспособным и продолжает деятельность, участок, утративший связь с телом, отмирает. Аксоны образуют нервы, что предполагает сложную структурно-морфологическую организацию ЦНС.
Строение
Аксон – это длинный отросток нейрона, который обеспечивает взаимодействие между нервными клетками. Согласно анатомии, аксон ответвляется от холмика, находящегося на теле. Холмик аксона представляет собой структуру, где постсинаптический потенциал преобразуется в биоэлектрический сигнал. Чтобы в холмике происходила генерация биоэлектрических сигналов, необходима согласованная деятельность каналов –натриевых, кальциевых, нескольких типов калиевых.
Длина аксона у человека существенно варьируется в зависимости от вида нейрона, от которого отходит аксональная ось. Минимальная длина – около 1 миллиметра, максимальная – около 1,5 метров. Длина более 1 метра наблюдается в случаях, когда отросток отходит от спинного мозга в область конечностей. Диаметр аксональной оси также неодинаковый у разных типов клеток, равен около 1-20 микрон. Импульсы проходят быстрее по аксональным осям большего диаметра.
Размеры аксонального отростка нередко достигают 99% от общего объема нервной клетки, в структуру которой он входит. Аксон состоит из протоплазмы (аксоплазмы), где находятся тончайшие волокна, белковые нити – нейрофибриллы, из чего образован ствол аксонального ответвления. Согласно одной из теорий, нейрофибриллы – проводники питательных веществ. Аксональная протоплазма также содержит митохондрии и микротрубочки, которые представляют собой самые крупные элементы цитоскелета.
Диаметр микротрубочек составляет около 24 нанометров. Они обеспечивают внутриклеточный транспорт веществ, в том числе поддерживают трофику аксональных отростков. Тело (перикарион) – источник протеинов и нейромедиаторов, распространяющихся по аксональной оси посредством микротрубочек, которые у аксона имеют направленную полярную ориентацию (в отличие от микротрубочек дендритов).
Положительно заряженные концы микротрубочек направлены к сегменту терминали, отрицательно заряженные концы – к телу. Строение аксона предполагает наличие оболочки. Аксон покрыт глиальным (миелиновым) слоем по всей длине, чем защищен от разрушающих внешних воздействий. Миелиновый слой в аксональных отростках периферического отдела сформирован клетками Шванна.
Миелиновая оболочка, покрывающая нервную ось, обеспечивает ее механическую прочность, электрохимическую изоляцию, трофику (питание). Миелиновый слой ускоряет проведение биоэлектрических сигналов. Нервы – пучки объединенных аксональных отростков, которые покрыты оболочкой из соединительной ткани и снабжены кровеносными сосудами.
Функции
Основная задача нейронов – переработка данных. С их помощью осуществляется получение, обработка, передача информации отделам нервной и других систем организма.
Если дендриты проводят сигналы по направлению к телу нервной клетки (перикариону), то аксональный отросток передает импульсы от перикариона к другим клеткам.
Основная функция аксонов – проведение импульсов в пределах нейрональной сети и к исполнительным органам. Аксональные ответвления относятся к первичным проводниковым путям в нервной системе. Вспомогательная функция – транспорт веществ. При помощи аксонального транспорта осуществляется движение белков, синтезированных в теле, нейромедиаторов, органелл. Многие вещества способны двигаться в обоих направлениях.
В периферических сегментах аксона в него могут проникать вирусы и токсичные вещества, которые перемещаясь к телу нервной клетки, повреждают ее. Аксональный транспорт зависит от количества энергии АТФ. Если энергетический уровень АТФ понижается больше, чем в 2 раза, происходит блокировка аксонального транспорта.
Функции аксона заключаются в передаче импульсов. При взаимодействии аксона с телом другого нейрона образуется аксосоматический контакт. Если аксон взаимодействует с дендритами других клеток возникает аксодендритический контакт. Взаимодействие с аксоном другой клетки приводит к образованию аксо-аксонального контакта, который редко происходит в нервной системе, поддерживает тормозные рефлекторные реакции.
Особенности регенерации нервной ткани
Нервные клетки почти полностью лишены способности к регенерации. Однако нервные клетки способны восстанавливать поврежденные или утраченные ответвления. Процесс регенерации аксона возможен, если тело сохраняет жизнеспособность, и на пути роста аксонального отростка отсутствуют препятствия. В ходе процесса регенерации отросток вновь прорастает к органу-мишени.
Восстановление нервной проводимости в мышцах с нарушенной иннервацией – один из критериев успешного лечения невропатий разного генеза. При невропатиях травматического генеза восстановление функций мышц происходит за счет регенерации ствола прерванного аксона и ремиелинизации отростка (восстановление миелиновой оболочки). Периферический отдел нервной системы обладает более высоким потенциалом регенерационных возможностей в сравнении с центральным отделом.
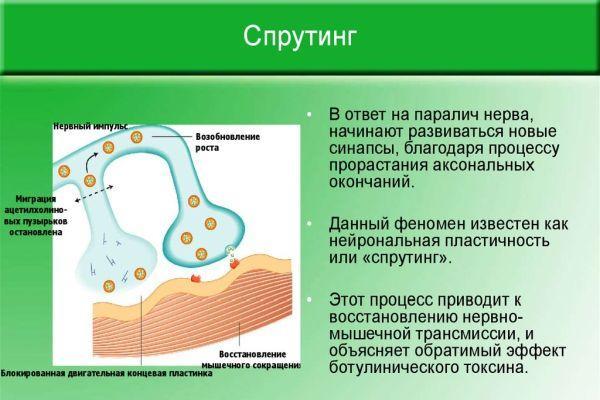
Восстановление иннервации в мышечной или кожной ткани происходит благодаря сохранившимся аксонам, которые начинают ускоренно разрастаться и ветвиться. Процесс ветвления аксонов в зоне перехватов Ранвье (периодические разрывы миелинового слоя) получил название «спрутинг». В результате происходит частичное или полное возобновление первичной иннервации.
В ходе экспериментов установлено, что близлежащие интактные (не вовлеченные в патологический процесс) аксоны выпускают нервные волокна, которые иннервируют участок мускулатуры или кожных покровов с нарушенной проводимостью нервных импульсов. Различают виды спрутинга – коллатеральный (обходной) и регенераторный (терминальный).
Регенераторный спрутинг начинается после устранения в нейронах ретроградных изменений, обусловленных аксонотомией (повреждением, рассечением нервной оси). Это связано с потребностью в продукции аппарата ядра нервной клетки, производящего протеины. Материал, необходимый для регенераторного спрутинга, продуцируется в теле и транспортируется по микротрубочкам по всей длине оси. Параллельно происходит процесс ремиелинизации осевого ствола.
Аксон – удлиненный отросток нервной клетки, обеспечивающий взаимодействие между структурными элементами мозговой ткани и связь ЦНС с исполнительными органами.
Просмотров: 2 336








 .
.



 .
.
![f(I)={begin{cases}0,Ileq I_{{mathrm {th}}}\{[}t_{{mathrm {ref}}}-R_{{mathrm {m}}}C_{{mathrm {m}}}log(1-{tfrac {V_{{mathrm {th}}}}{IR_{{mathrm {m}}}}}){]}^{{-1}},I>I _ { mathrm {th}}} end {ases}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c28e40bb941f3613b8c21d2935284f1b32aaff03)
![{ displaystyle tau _ { mathrm {m}} { frac {dV _ { mathrm {m}} (t)} {dt} } = RI (t) - [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] - R sum _ {k} w_ {k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f8345759b126e0ae20788d2be0b5f74b89dd598)
![{ d isplaystyle tau _ {k} { frac {dw_ {k} (t)} {dt}} = - a_ {k} [V_ { mathrm {m}} (t) -E _ { mathrm {m} }] - w_ {k} + b_ {k} tau _ {k} sum _ {f} delta (tt ^ {f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8561a663fc284164af5004d49dda606de65f3153)

![{ displaystyle { frac {dV} {dt}} - { frac {R} { tau _ {m}}} I (t) = { frac {1} { tau _ {m}}} [E_ {m} -V + Delta _ {T} exp left ({ frac {V-V_ {T}} { Delta _ {T}}} right)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/86f691681dd09ecbcdb84ddae90a2e507f19afc1) .
.![{ displaystyle tau _ {m} { frac {dV} {dt}} = RI ( t) + [E_ {m} -V + Delta _ {T} exp left ({ frac {V-V_ {T}} { Delta _ {T}})} right)] - Rw}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e10f63ab5b4efb55134e43e41eb146b570651960)
![{ displaystyle tau { frac {dw (t)} {dt}} = - a [V _ { mathrm {m}} (t) -E _ { mathrm {m}}] - w + b tau delta (tt ^ {f})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ad1061c0bd8fa3f0894982dfd5913c5114471f9)





![{ displaystyle tau _ { mathrm {m}} { frac {dV _ { mathrm {m}} (t)} {dt}} = (I-I_ {0}) R + [V _ { mathrm {m }} (т) -E _ { mathrm {m}}] [V _ { mathrm {m}} (t) -V _ { mathrm {T}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8392a8de9357950491d89517ec59294d6ef35e5)
 ,
,
 ,
,


 .
.![{displaystyle P_{spike}(tin [t',t'+Delta _{t}])=Delta _{t}cdot g[s(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20e225ceaf3666cc8be1af1e0764ffe48fbe0475)
![{ Displaystyle R_ {огонь} (т) = { гидроразрыва {P_ {шип} (т; Delta _ {t})} { Delta _ {t}}} = [y (t) + R_ {0}] cdot P_ {0} (t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32a68d5cc75b6acd50495998a27b695e17d803a)
![{ displaystyle { dot {P}} _ {0} = - [y (t) + R_ {0} + R_ {1}] cdot P_ {0} (t) + R_ {1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/830fe4d93362af37a7b4d97c1902b7db1826f9e1)