Статья на конкурс «био/мол/текст»: Тайна того, каким образом «работает» человеческий мозг, мучила философов и естествоиспытателей с древнейших времен. Современные ученые постепенно подходят к ее разгадке, приближая тот час, когда мы сможем полностью понять, как и с помощью чего мы на самом деле думаем. Именно сейчас развитие вычислительной техники и последние достижения в нейробиологии сделали реальным то, что раньше казалось недостижимым. Появились компьютеры, способные понимать речь, ориентироваться в пространстве и даже писать научные статьи. Работа таких машин частично основана на принципах работы головного мозга. Каким образом они работают, что такое мышление и где оно происходит? Обо всем этом мы попытаемся рассказать.
Клетки-деревья
Общеизвестно, что наш мозг состоит из нейронов (по крайней мере, именно они отвечают за мыслительный процесс). Морфологически эти клетки похожи на деревья с корнями-дендритами и стволом-аксоном. На дендритах суммируются электрические сигналы, поступающие от других нейронов, и в зависимости от этого нейрон «принимает решение», формировать ли ему потенциал действия (т.е. нервный импульс). Потенциалом действия называется волна токов ионов натрия и калия, которая быстро проходит через мембрану и распространяется без затухания по аксону к другим нейронам. Именно это свойство позволяет нейронам передавать сигнал без потери информации на большие расстояния. Так, потенциал действия, сформированный в коре головного мозга, может достичь нейронов в позвоночнике, а затем в руке, за считанные миллисекунды. В окончании аксона находятся синапсы, из которых после прохождения потенциала действия высвобождаются особые вещества — нейромедиаторы. Именно они передают сигнал к следующему нейрону, и так далее, по цепочке [14].
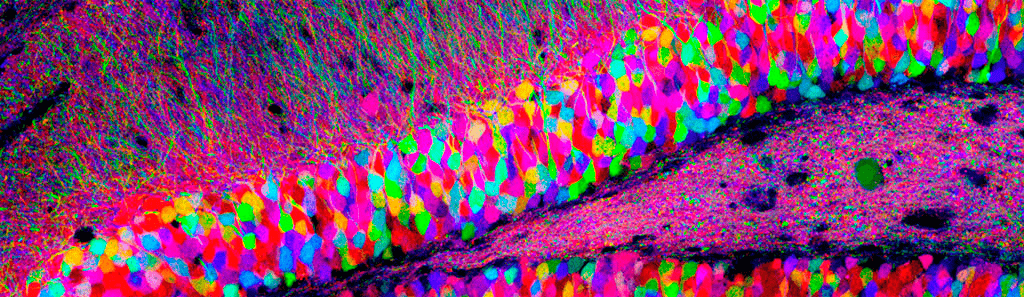
Однако один нейрон сам по себе не способен обеспечить сложное поведение, характерное для животных и тем более самого умного из них — человека. По оценкам ученых, в человеческом мозге около 100 миллиардов нервных клеток, которые соединены в сложнейшую сеть со 100 триллионами синаптических контактов между ними (рис. 1). При виде таких чисел в пору отчаяться и бросить попытки разобраться в том, как функционирует этот сложнейший природный объект. К счастью, ученые — люди не робкого десятка и продолжают упорно двигаться вперед.
Рисунок 1. Множество нейронов в срезе гиппокампа крысы. Клетки помечены различными флуоресцентными белками с помощью технологии Brainbow.
Моделирование вместо опыта
Один из главных вопросов изучения биологических нейронных сетей — каким образом при соединении нейронов относительно простое поведение отдельной единицы трансформируется в сложное поведение сети в целом. Однако полностью разобраться в этом мешают ограниченные возможности эксперимента: в настоящей нейронной сети практически невозможно измерить все сигналы со всех 100 миллиардов нейронов и отследить все процессы, происходящие в ней. Тут-то на помощь ученым и приходит компьютерное моделирование. Математические модели всегда помогали исследователям отвечать на подобного рода сложные вопросы. А после появления вычислительных машин возможности в этой области постоянно расширяются.
Одним из последних достижений в этой области является проект Blue Brain, возглавляемый Генри Маркромом [2], [3]. В рамках этой инициативы ученые пытаются воспроизвести поведение одной колонки кортекса, состоящей из сотен тысяч клеток, которые моделируются с максимальной степенью детализации. Колонки в новой коре являются ее важнейшим функциональным элементом, на уровне которых, по мнению многих ученых, происходят вычисления, которые являются основой высших психических функций, включая мышление. Именно поэтому детальное изучение этих структур является крайне важным.
Первая модель работы нейрона была создана еще в 1907 году французским физиологом Льюисом Лаписиком [4] — задолго до того, как был изучен механизм формирования нейроном потенциала действия [5]. Модель была очень простой: согласно ей нейрон как конденсатор накапливает напряжение до определенного порогового значения, после чего генерирует потенциал действия. Стоит отметить, что концепция работы нейрона как порогового интегратора почти не изменилась после публикации работы Льюиса Лаписика, но было выяснено множество важнейших деталей.
Нобелевская премия за кальмара
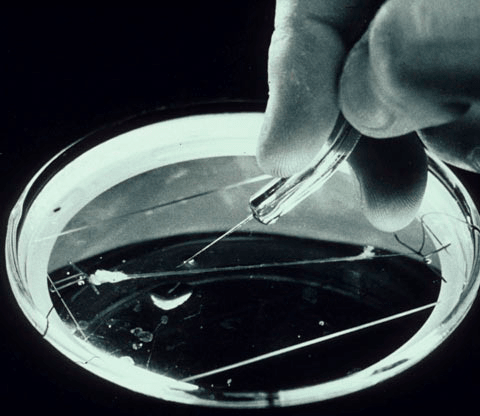
Однако наибольшее распространение получила модель Ходжкина-Хаксли, построенная на основе экспериментов с гигантским аксоном кальмара [5] (рис. 2). Тут мы позволим себе небольшое отступление, чтобы рассказать о том, почему нейроны именно этого живого организма оказались такими удобными для исследований.
Рисунок 2. Гигантский аксон кальмара в чашке Петри. Может быть, на первый взгляд он и не кажется таким уж большим, но по сравнению с аксонами нейронов головного мозга, которые невозможно увидеть невооруженным глазом, он просто огромен.
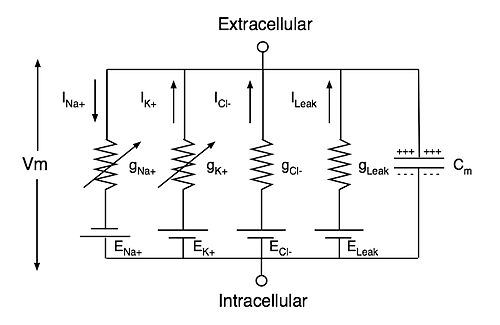
Модель Ходжкина-Хаксли (рис. 3) описывает поведение нейрона, представляя его в виде достаточно простой электрической цепи, где мембрана является конденсатором, ионные каналы — проводимостями (величина, обратная сопротивлению, измеряемая в Сименсах), градиенты ионов натрия, калия и хлора на мембране (то есть, разница между концентрацией ионов внутри и снаружи) — источниками напряжения. При этом активируемые каналы для ионов калия, натрия и хлора описываются нелинейными проводимостями gK, gNa и gCl, а каналы утечки, которые открыты всегда, — постоянной проводимостью gL (от англ. leak — «утечка»). Полученная модель работы нейрона оказалась применима не только для кальмара, но и для млекопитающих, в том числе для человека. Поэтому авторы исследования — британцы Алан Ходжкин и Эндрю Хаксли — получили в 1963 году Нобелевскую премию по физиологии и медицине.
Рисунок 3. Схема электрической цепи модели Ходжкина—Хаксли гигантского аксона кальмара, за которую была получена Нобелевская премия в 1963 году. Cm — емкость мембраны нейрона, ENa+, EK+, ECl− и ELeak — потенциалы реверсии токов натрия, калия, хлора и утечки, а gNa+, gK+, gCl− и gLeak — соответствующие проводимости ионных каналов. Vm — трансмембранный потенциал.
От подневольного труда к искусственному интеллекту
Первые упоминания об искусственных разумных существах можно обнаружить еще в греческой мифологии. Согласно легендам, Гефест по просьбе Зевса создал бронзового гиганта Талоса (рис. 4), который охранял Елену на острове Крит. В средние века появились предания о гомункулусах и Големе — созданных человеком разумных существах.
Рисунок 4. Бронзовый гигант Талос — пожалуй, первый робот в мифологическом фольклоре (кадр из фильма «Ясон и аргонавты», 1965 год).
С конца XIX века искусственные живые существа стали неотъемлемой частью культуры, начиная с «Франкенштейна» Мэри Шелли и пьесы Карела Чапека (рис. 5) «R.U.R.» («Россумские Универсальные Роботы»). Кстати, именно в этой пьесе Чапек впервые использовал придуманное с братом Йозефом слово «робот» (по-чешски robota означает «подневольный труд»).
Рисунок 5. Монстр Франкенштейна (а), Карел Чапек (б) и Алан Тьюринг (в)
До середины XX века разговоры о разумных машинах носили чисто теоретический характер, но уже в 1956 году разработка искусственного интеллекта приобрела статус научной дисциплины. Произошло это благодаря появлению электронных вычислительных машин, а также прорыву в нейробиологии. Наука о мозге помогла понять, что нервная система функционирует благодаря обмену нейронов электрическими импульсами, а вычислительные машины позволили описывать эти процессы с помощью программ.
Вскоре стало понятно, что создание искусственного интеллекта требует как минимум понимания значений слов «искусственный» и «интеллект». Алан Тьюринг нашел элегантный выход: вместо того, чтобы пытаться сформулировать, что же такое «интеллект», он предложил определять, есть он у машины или нет, способом, который получил название «Тест Тьюринга» [8].
Идея теста заключается в том, что экзаменатор общается в текстовом режиме с двумя испытуемыми, один из которых — машина, а другой — человек. Цель экзаменатора — определить, кто есть кто. Тест считается успешным, если машине удается обмануть эксперта. Несмотря на кажущуюся простоту, ни одной программе до сих пор не удалось его пройти.
Хотя настоящего думающего робота создать пока не удалось, различные современные подходы позволяют непрерывно расширять область задач, которые способны решать компьютеры, даже в тех сферах, которые всегда считались доступными лишь людям — например, работа с символами и написание научных статей.
Символьный подход
Первые достижения в создании искусственного интеллекта были связаны с использованием возможностей математической логики. Уже в 1956 году была создана программа с говорящим названием Logic Theorist, которая смогла доказать 38 из 52 теорем, описанных в книге Бертрана Рассела и Альберта Уайтхэда «Основания математики», причем для некоторых из них она смогла найти новые, более простые доказательства. В это же время были созданы программы, способные правдоподобно имитировать переписку с живым человеком (правда, недостаточно хорошо для прохождения теста Тьюринга), и многие другие.
Все эти программы основывались на предположении, что интеллект заключается в осуществлении операций над различными символами по законам логики. На этом принципе были основаны первые коммерчески успешные программы искусственного интеллекта — экспертные системы. Они позволяли частично заменить работу реального эксперта — например, оценить риск организации при предоставлении кредита клиенту. Такая программа работает с базой знаний (набором фактов и правил, формализующих работу экспертов в данной области) по определенным логическим законам. Но далеко не все проблемы могут быть решены в рамках строгой логики, поэтому зачастую в таких программах используется нечеткая или вероятностная логика. Ее особенностью является то, что вместо 0 и 1 — «да» или «нет» — в ней используются все значения между 0 и 1, — например, 0.2 или 0.7: «скорее да», «скорее нет».
Весьма ограниченный успех логического подхода продемонстрировал одну важную вещь: интеллект — это не только способность логически мыслить. Поэтому для решения сложно формализуемых задач (например, распознавания образов) пришлось отказаться от красоты и стройности формальной логики.
Нейронные сети
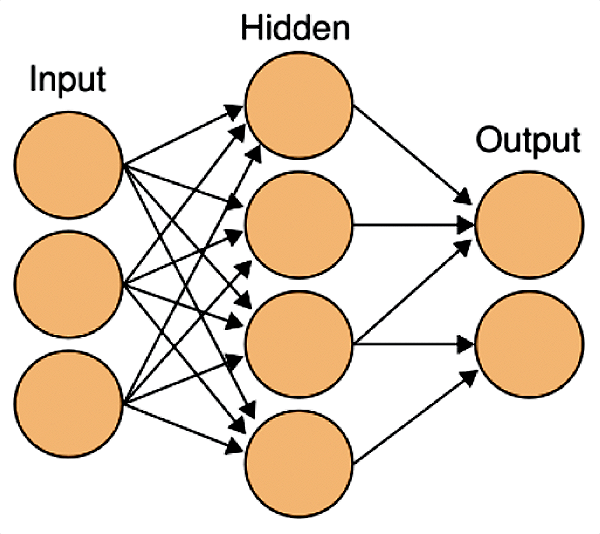
Разработчики искусственных нейронных сетей были вдохновлены работой настоящих нейронов в мозге. Только вместо реальных клеток в сетях используются уравнения, моделирующие их работу (рис. 6).
Рисунок 6. Схема искусственной нейронной сети. На входные нейроны подается стимул, затем он обрабатывается в нейронах скрытого слоя (таких слоев может быть несколько) и результаты предоставляются на выходных нейронах.
Первыми в нейронной сети получают информацию входные нейроны. Именно они получают сигналы от внешнего стимула, который может быть всем, чем угодно: изображения, отдельные звуки и даже человеческая речь. Но для того, чтобы передать полученную информацию, входным нейронам необходимо перевести сигнал стимула на их «язык». Это уже работа другого вида клеток — рецепторов, которые преобразуют информацию о стимуле в нервные импульсы. Биологическим примером таких рецепторов являются палочки и колбочки в сетчатке глаза. Подобные рецепторы есть и в искусственных нейронных сетях: при обработке изображений это фотоэлементы, звуков — микрофоны.
Конечным этапом обработки информации в нейросети являются выходные нейроны, активность которых интерпретируется как результат: преобразованный входными нейронами сигнал от рецепторов попадает в сеть, затем переходит к следующим нейронам и преобразуется за счет взаимодействий между ними через синапсы. Например, если сеть занимается распознаванием букв алфавита, то после успешного обучения на выходе будут активны нейроны, соответствующие этим буквам.
Для того чтобы сеть могла правильным образом классифицировать входной сигнал, связи между нейронами должны быть правильно подобраны. В 1943 году нейрофизиолог Фрэнк Розенблатт создал модель, которая называется перцептрон (от лат. perceptio — восприятие) [9]. Она работает следующим образом: в начале обучения связи между нейронами являются одинаковыми, затем сети предъявляются различные буквы по нескольку раз, и если буквы классифицируются на выходных нейронах правильно, то связи, приводящие к правильной классификации, усиливаются, а если нет, то ослабляются [13]. Таким образом, после предъявления большого количества стимулов сеть учится их распознавать. При этом, чем больше букв необходимо выучить сети, тем бóльшим должно быть количество нейронов. В качестве результата сеть может распознавать буквы, которые лишь отдаленно напоминают те, которые использовались при обучении. Более того, буквы могут быть повреждены или написаны другим шрифтом, но сеть все равно будет способна их распознать!
На самом деле многие программы в компьютере используют такой подход: например, программа Fine Reader, которая распознает изображение и переводит его в текст, использует в своей работе нейросети. По такому же принципу работает распознавание рукописного ввода на смартфонах и планшетах.
Генетические алгоритмы
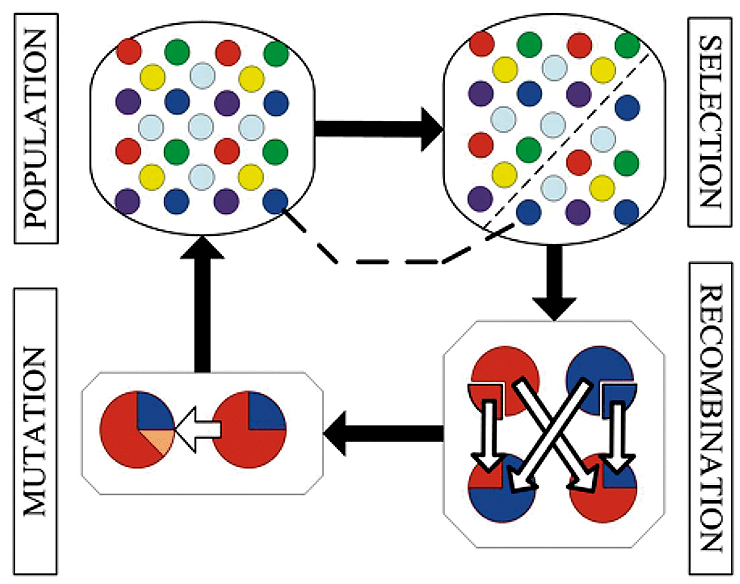
Еще одним подходом в программировании, вдохновленным биологией, являются эволюционные алгоритмы (рис. 7). В рамках этого подхода занимаются моделированием процесса биологической эволюции, только вместо живых организмов используются программы [10]. На первый взгляд у алгоритмов и животных мало общего, но, если присмотреться, можно увидеть похожее.
Под алгоритмом в общем случае подразумевают последовательный набор действий, который приводит к желаемому результату за конечное число ходов. Например, чтобы прийти в университет, необходимо: 1) проснуться, 2) умыться, 3) одеться, 4) позавтракать, 5) собраться, 6) пойти. Конечно, детали алгоритмов могут быть разными: например, кому-то не нужно собирать вещи, потому что они были собраны вчера. Но важным является то, что в любом случае выполняется последовательность действий, приводящая к нужному результату.
Рисунок 7. Принцип работы генетических алгоритмов. В начале рассматривается популяция алгоритмов, которые выполняют определенную задачу. Затем вводится правило, в соответствии с которым селективно выбираются только те из них, которые способны выполнить задачу лучше других. Затем алгоритмы обмениваются отдельными частями, чтобы получить новые на этапе рекомбинации. После этого на этапе мутаций в алгоритмы вносятся небольшие случайные изменения, чтобы увеличитель их разнообразие. Затем процедура выбора алгоритмов повторяется много раз, и на завершающем этапе остаются только те алгоритмы, которые выполняют задачу наилучшим образом.
Для того, чтобы алгоритмы могли эволюционировать, их разделяют на отдельные части, которые можно менять между собой. Например:
- проснуться—умыться—одеться—позавтракать—собраться—пойти;
- проснуться—собраться—одеться—позавтракать—умыться—пойти и т.д.
Также необходимо отказаться от невозможных вариантов: к примеру, алгоритм «одеться→позавтракать→проснуться→…» невозможен по понятным причинам.
После этого оценивают работу каждого алгоритма и выбирают наилучший. К примеру, в случае с походом в университет лучшим алгоритмом будет самый быстрый. Затем производится обмен их частей между собой и внесение мутаций (добавление и/или видоизменение действий), после чего появляются новые алгоритмы, которые снова оцениваются. Таким образом, через несколько поколений отбираются именно те, которые справляются с задачей лучше всего. Такие алгоритмы часто используют в биоинформатике, инженерном деле и многих других приложениях, чтобы находить наилучшие решения.
Во что играть против робота?
В 1994 году программа Chinook стала чемпионом мира по шашкам, впоследствии защитив этот титул в 1996 году. В 2007 году команда разработчиков Chinook закончила полный анализ всех возможных комбинаций этой игры, и Chinook стала непобедимой. На сегодняшний день шашки — самая сложная полностью проанализированная игра; в ней имеется 5×1020 возможных комбинаций фигур на игровом поле.
Но не стоит отчаиваться, потому что все еще существуют игры, в которых человек легко побеждает компьютер [11]. Например, к ним относится китайская игра го (рис. 8). Выглядит она достаточно просто: поле состоит из сетки 19×19 и двух видов шашек: черных и белых. Целью игры является захват территории — это чем-то напоминает игру в точки. Однако, несмотря на простоту правил, ней существует огромное количество возможных комбинаций. Если в шахматах после четвертого хода от начала партии может возникнуть несколько сотен тысяч различных вариантов, то в го их число превышает шестнадцать миллиардов. Так что пока человек все еще непобедимый соперник в некоторых играх против компьютера.
Рисунок 8. Игра го считается одной из наиболее сложных логических игр для освоения компьютером. Уже средние игроки легко побеждают любые существующие на данный момент компьютерные программы.
Заменят ли роботы ученых?
Казалось бы, кому, как не ученым, меньше всего стоит бояться того, что машины смогут конкурировать с ними? Не тут-то было: программисты из Массачусетского технологического института создали программу под названием SCIgen, способную «писать» тексты, посвященные разработке новых компьютерных алгоритмов, с иллюстрациями, графиками, ссылками и всеми остальными необходимыми атрибутами [12]! Правда, эти тексты похожи на научные статьи лишь по форме, а их осмысленность стремится к нулю.
Авторы создали эту программу для того, чтобы вывести на чистую воду конференции, которые публикуют присылаемые на них тезисы не глядя, и им это удалось. Тексты, сгенерированные программой, были приняты к публикации в сборниках тезисов сразу нескольких конференций. Группа российских ученых решила проверить, насколько тщательно подходят к отбору статей в отечественных журналах, и перевела текст, сгенерированный SCIgen, на русский язык. В итоге «статья» под названием «Корчеватель: Алгоритм типичной унификации точек доступа и избыточности» была опубликована в «Журнале научных публикаций аспирантов и докторантов»!
Разумные роботы уже рядом
Итак, полным ходом идет работа над созданием искусственного интеллекта — программ, обладающих, хотя бы частично, свойствами человеческого интеллекта. Пока что лучше всего ученым удается решение конкретных специализированных задач, таких как распознавание образов, автоматизированное написание финансовых отчетов или описание итогов спортивных игр на основе статистических данных о ходе игры.
Однако создание так называемого «сильного» искусственного интеллекта, то есть полноценного искусственного сознания, до сих пор представляется трудно достижимой целью. Тем не менее попытки его создания чрезвычайно полезны, так как позволяют лучше понять, что такое человеческий разум. Сегодня основная работа направлена на создание алгоритмов, позволяющих компьютерам осуществлять логические размышления, собирать, систематизировать и оперировать знаниями об окружающем мире, ставить цели и искать оптимальные пути их достижения, обучаться, распознавать речь и многое другое. «Сильный» искусственный интеллект должен объединять все эти алгоритмы и осуществлять взаимодействие между ними. При этом современные тенденции развития в этой области свидетельствуют о том, что, если «сильный» искусственный интеллект будет создан, большую роль в его создании будут играть нейронные сети, а значит, мы вряд ли будем знать в точности, как он работает. Стоит также отметить любопытное явление: многие успехи в развитии искусственного интеллекта, которые казались невозможными ранее, после их достижения не воспринимаются как «О, это же действительно искусственный разум!» Так что вполне возможно, что мы просто не заметим появление разумных роботов.
Статья написана в соавторстве с Антоном Сабанцевым. Частично материалы статьи были опубликованы в журнале «Я — Леонардо» (лето—осень 2013).
- Jean Livet, Tamily A. Weissman, Hyuno Kang, Ryan W. Draft, Ju Lu, et. al.. (2007). Transgenic strategies for combinatorial expression of fluorescent proteins in the nervous system. Nature. 450, 56-62;
- Henry Markram. (2006). The Blue Brain Project. Nat Rev Neurosci. 7, 153-160;
- Blue Brain Project: как все связано?;
- Nicolas Brunel, Mark C. W. van Rossum. (2007). Lapicque’s 1907 paper: from frogs to integrate-and-fire. Biol Cybern. 97, 337-339;
- A. L. Hodgkin, A. F. Huxley. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of Physiology. 117, 500-544;
- О чем не знал Гальвани: пространственная структура натриевого канала;
- Формирование мембранного потенциала покоя;
- Alan M. Turing. (2009). Computing Machinery and Intelligence. Parsing the Turing Test. 23-65;
- F. Rosenblatt. (1958). The perceptron: A probabilistic model for information storage and organization in the brain.. Psychological Review. 65, 386-408;
- Barricelli N.A. (1957). Symbiogenetic evolution processes realized by artificial methods. Methodos. 9, 143–182;
- Johnson G. (1997). To test a powerful computer, play an ancient game. The New York Times;
- Cyril Labbé, Dominique Labbé. (2013). Duplicate and fake publications in the scientific literature: how many SCIgen papers in computer science?. Scientometrics. 94, 379-396;
- Hebb D.O. The organization of behavior: A neuropsychological theory. Psychology Press, 2002;
- Kandel E.R. et al. Principles of neural science. NY: McGraw-Hill, 2000.
В гигантском аксоне кальмара:
Концентрац ия внутри клетки
340
ммоль/л
49
ммоль/л
114
ммоль/л
Концентрация
во
внеклеточной
среде
10
ммоль/л
463
ммоль/л
592
ммоль/л
•2) В покое проницаемость
наружной мембраны клетки для
ионов калия значительно больше, чем для натрия, и больше, чем для ионов хлора:
• Например, для аксона кальмара:
РК : РNa : PCl = 1 : 0,04 : 0,45
•Такая проницаемость обусловлена наличием в наружной мембране так называемых
потенциалнезависимых каналов, избирательно пропускающих ионы калия, натрия или хлора.
•Если концентрация какого-либо иона внутри клетки отлична от концентрации этого иона снаружи, и мембрана проницаема для этого иона, возникает поток заряженных частиц через мембрану.
•Происходит пространственное разобщение противоположных по знаку ионов.
•Вследствие этого электрическая нейтральность системы нарушается, образуется разность
потенциалов (градиент потенциала) между наружной и внутренней средой, которая
препятствует дальнейшему
переносу ионов через мембрану.
•При установлении равновесия между
концентрационным и электрическим градиентом выравниваются значения
электрохимических потенциалов по разные стороны мембраны и устанавливается равновесный потенциал для этого иона, который рассчитывается по формуле Нернста.
μ= μ0 + RTlnC + zFφ
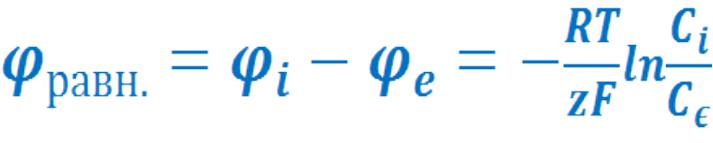
• При равновесии:
RTlnCi + zFφi = RTlnCe + zFφe
• Отсюда:
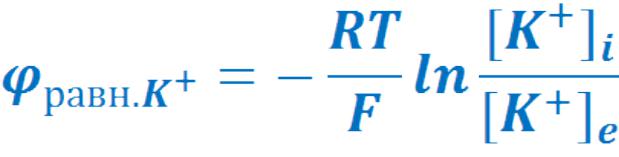
•Если принять, что мембранный потенциал обусловлен только переносом ионов калия, то
калиевый равновесный потенциал равен:
•Расчеты показывают, что для создания такого равновесного потенциала через мембрану клетки должно пройти всего
10-4 % ионов калия от общего их содержания внутри клетки (изменение концентрации калия всего на 2.10-3 ммоль/л).
•Это пренебрежимо малое количество ионов калия по сравнению с общим их количеством в клетке.
Соседние файлы в папке Презентации
- #
- #
- #
- #
- #
- #
- #
- #
Мало какое животное сыграло такую важную роль в развитии нейробиологии, как кальмар. А точнее — гигантский аксон в его мантии, аксон нейрона, который отвечает (в том числе), за реактивную систему кальмара. Этот аксон достигает в диаметре до полутора миллиметров (обычно полмиллиметра). Его открывали дважды: сначала аксон описал в 1909 году Леонард Уорчестер Уильямс, но открытие не заметили и забыли — и только через 27 лет британец Джон Юнг заново открыл его, и знаменитые Ходжкин и Хаксли получили материал, при помощи которого они построили модель потенциала действия и получили свою Нобелевскую премию 1963 года.
«Можно утверждать, что введение Юнгом в 1936 году препарата аксона кальмара имело для науки об аксоне большее значение, чем какое-либо другое открытие, сделанное за последние 40 лет. Один выдающийся нейрофизиолог заметил недавно во время ужина на одном из конгрессов (не самым тактичным образом, должен признать): «Если честно, Нобелевскую премию нужно было присвоить кальмару»», — вспоминал Ходжкин.
Нам попалось видео, в котором вы можете увидеть анатомирование кальмара и Тот Самый Аксон. А анатомирование проводит Тот Самый Джон Янг, «один из самых влиятельных биологов ХХ века».
|
|
Макеты страниц
Свойства полной модели Ходжкина — Хаксли, как правило, изучались с помощью расчетов на ЦВМ. Так как модели второго порядка хорошо описывают свойства моделей четвертого порядка, оценки свойств решений исходных уравнений можно легко получить по графикам нуль-изоклин уравнений второго порядка. Ниже будет продемонстрировано, как самые различные электрофизиологические явления могут быть объяснены не только качественно, но и количественно в терминах фазовых портретов редуцированных моделей.
Спонтанная активность. Известно, что в клетках, не обладающих спонтанной активностью, последняя может быть вызвана, например, увеличением натриевой или уменьшением калиевой
Анализ основан на том, что спонтанная активность в модели четвертого порядка 


Изоклины системы 

Обратим внимание, что, как следует из формулы (4.6), на форму изоклины 




Устойчивая деполяризация мембраны. Увеличение натриевого тока (например, за счет сдвига 

Исследование устойчивости деполяризации в модели Ходжкина — Хаксли, в принципе, ничем не отличается от исследования спонтанной активности. Здесь необходимо определить, при каких изменениях параметров модели мембраны 


Повторные ответы. Известно [21, 22], что в гигантском аксоне кальмара и в других мембранах автоколебания могут возникать под действием внешнего тока; в этом случае их называют повторными ответами. А возможны ли повторные ответы в модели Ходжкина — Хаксли? В каком диапазоне токов? Каков их механизм?
правую и вновь становится устойчивой. Повторные ответы прекращаются, возникает устойчивая деполяризация под током (рис. 35).
Интересно, что на некоторых биологических мембранах (перехват Ранье, модифицированный аконитином [36], препараты папиллярной мышцы сердца [37] и др.) повторные ответы не удается вызвать ни 


Скачкообразная деполяризация. При плавном повышении концентрации 


Триггерные свойства мембраны. Аксон кальмара при некоторых экспериментальных условиях, например при внутриклеточной перфузии 

Аккомодация. Этим термином называют свойство мембраны увеличивать порог возбуждения при длительном действии тока. Выделяют три типа мембран [33]: абсолютно аккомодирующие (при стимуляции линейно нарастающим током 
исследуемых значений 






Оглавление
- ОТ АВТОРОВ
- ВВЕДЕНИЕ
- 1. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ БИОХИМИЧЕСКИХ СИСТЕМ
- Глава первая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 1.2. Ферменты — белковые катализаторы и регуляторы
- 1.3. Метод графов
- 1.4. Модели реакций, катализируемых одноцентровыми ферментами
- 1.5. Модели реакций, катализируемых олигомерными ферментами
- 1.6. Свойства реакции …
- 1.7. Свойства двухсубстратной реакции
- Глава вторая. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОТОЧНЫХ ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ
- 2.2. Модель открытой реакции … с субстратным угнетением
- 2.3. Модель двухсубстратной реакции с субстратным угнетением
- 2.4. Динамика открытых реакций, катализируемых олигомерными ферментами
- 2.5. Разнообразие поведения открытых ферментативных реакций
- 2.6. Эквивалентные математические и кинетические модели
- 2.7. Эффект депонирования
- Глава третья. МОДЕЛИРОВАНИЕ ПОЛИФЕРМЕНТНЫХ СИСТЕМ
- 3.1. Полиферментные системы и их модели
- 3.2. Уровни функциональной организации полиферментных систем
- 3.3. Простая модель стехиометрической структуры энергетического метаболизма
- 3.4. Два класса аллостерических регуляторных связей, контролирующих энергетический метаболизм
- 2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВОЗБУДИМЫХ МЕМБРАН
- Глава четвертая. КАЧЕСТВЕННЫЕ МЕТОДЫ В ИССЛЕДОВАНИИ МОДЕЛЕЙ МЕМБРАН
- 4.1. Построение уравнений второго порядка для моделей Ходжкина — Хаксли и Побла
- 4.2. Фаэовые портреты систем второго порядка
- 4.3. Исследование основных режимов мембраны аксона кальмара с помощью качественных методов
- 4.4. Исследование основных режимов мембраны волокна Пуркинье сердца с помощью качественных методов
- 4.5. Математические детали асимптотического сведения уравнений Ходжкина — Хаксли к системе второго порядка Н-Н2
- Глава пятая. БИОЛОГИЧЕСКИ АКТИВНЫЕ ВЕЩЕСТВА, ИОННЫЕ ТОКИ И ЭЛЕКТРОФИЗИОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ МЕМБРАН
- 5.2. Техника анализа мембран по записям ионных токов
- 5.3. Фазовые портреты мембран сердечной, нервной и мышечной клеток
- 5.4. Анализ действия веществ на мембраны
- 5.5. Предсказание электрофизиологических эффектов с помощью качественных методов
- 5.6. Границы применимости анализа, мембран по фазовому портрету
- 5.7. Оценка на математических моделях мембран точности построения фазового портрета по записям ионных токов
- 3. ВОЗБУДИМЫЕ СРЕДЫ. ВОЛНЫ И АВТОВОЛНОВЫЕ ПРОЦЕССЫ
- 6.1. Автоволновые процессы в возбудимых средах
- 6.2. Распространение волн в однородной среде. Спиральная волна, вращающаяся вокруг отверстия, и ревербератор
- 6.3. Возникновение ревербератора в простейшей неоднородной среде
- 6.4. Ревербератор в более детальных моделях
- 6.5. Свойства ревербератора как источника волн. Размножение ревербераторов в неоднородной среде. Бремя жизни
- 6.6. Ревербератор и сердечные аритмии. Уязвимость сердечной ткани
- Глава седьмая. ЭХО – ИСТОЧНИК КОНЦЕНТРИЧЕСКИХ ВОЛН В ВОЗБУДИМЫХ СРЕДАХ
- 7.1. Эхо в простейших моделях. Источник эха и ревербератор
- 7.2. Источник эха в моделях, описываемых обыкновенными дифференциальными уравнениями
- 7.3. Эхо в непрерывных возбудимых средах
- 7.4. Эхо в модели клеток сердца. Уязвимость
- Глава восьмая. ВЗАИМОДЕЙСТВИЕ ИСТОЧНИКОВ ВОЛН. АВТОВОЛНОВЫЕ ПРОЦЕССЫ И СЕРДЕЧНЫЕ АРИТМИИ
- 8.2. Синхронизация при взаимодействии источников волн
- 8.3. Размножение ревербераторов и фибрилляция
- 8.4. Взаимодействие источников эха
- 8.5. Связь параметров возбудимых сред с характеристиками дифференциального уравнения мембраны
- 8.6. Стационарные и нестационарные режимы распространения
- 8.7. Результаты микроэлектродного исследования уязвимости
- 8.8. О параметрах, контролирующих уязвимость в математических моделях и в миокарде
- 8.9. Следствия из моделей для антиаритмических веществ
- 4. ПРОСТРАНСТВЕННАЯ ОРГАНИЗАЦИЯ БИОЛОГИЧЕСКИХ СТРУКТУР
- Глава девятая. МОДЕЛИРОВАНИЕ ОБЪЕМНЫХ КЛЕТОЧНЫХ СТРУКТУР. ВИРУСЫ, ФЕРМЕНТЫ
- 9.2. Математические основы объемной реконструкции
- 9.3. Модель трехмерной структуры отростка бактериофага
- 9.4. Голографический синтез объемного изображения поверхности клеточной мембраны
- 9.5. Моделирование структуры биологических макромолекул
- Глава десятая. АНАЛИЗ КЛЕТОЧНЫХ СТРУКТУР ПО ИХ ИЗОБРАЖЕНИЯМ. ГЛИЯ—СОСУДЫ, ХРОМОСОМЫ
- 10.1. Преобразование изображений клеток в цифровую форму
- 10.2. Определение морфометрических параметров клеток и клеточных структур
- 10.3. Исследование глиально-сосудистой системы головного мозга
- 10.4. Модель сокращения длины хромосом в митозе
- Глава одиннадцатая. ВОССТАНОВЛЕНИЕ ЛИНЕЙНОЙ СТРУКТУРЫ БИОПОЛИМЕРОВ
- 11.1. Анализ первичной последовательности нуклеиновых кислот
- 11.2. Математическая постановка проблемы
- 11.3. Восстановление слов по составу второго ранга
- 11.4. Метод подстановки при восстановлении слов
- 11.5. Оптимизация биохимического эксперимента