Нейрон Маккаллока-Питтса — первая математическая модель биологического нейрона человечества
Перевод
Ссылка на автора
Хорошо известно, что наиболее фундаментальная единица глубоких нейронных сетей называетсяискусственный нейрон / персептрон, Но самый первый шаг кперсептронмы используем сегодня был взят в 1943 году McCulloch и Pitts, имитируя функциональность биологического нейрона.
Примечание: концепция, содержание и структура этой статьи были в значительной степени основаны на удивительных лекциях и материалах, предложенных проф. Митеш М. Хапра на NPTEL «s Глубокое обучение курс. Проверьте это!
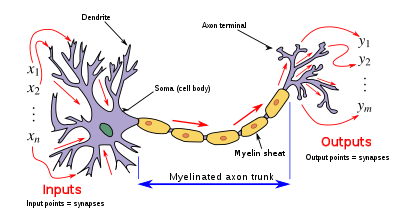
Биологические нейроны: чрезмерно упрощенная иллюстрация
дендрит: Получает сигналы от других нейронов
сома: Обрабатывает информацию
аксон: Передает вывод этого нейрона
синапс: Точка подключения к другим нейронам
По сути, нейрон принимает входной сигнал (дендрит), обрабатывает его подобно ЦП (сома), передает выходной сигнал через структуру, похожую на кабель, на другие подключенные нейроны (аксон для синапса к дендриту другого нейрона). Теперь, это может быть биологически неточно, поскольку там происходит гораздо больше, но на более высоком уровне это то, что происходит с нейроном в нашем мозгу — принимает входные данные, обрабатывает их, выбрасывает выходные данные.
Наши органы чувств взаимодействуют с внешним миром и посылают визуальную и звуковую информацию в нейроны. Допустим, вы смотрите Друзья. Теперь информация, которую получает ваш мозг, воспринимается набором нейронов «смеяться или нет», которые помогут вам принять решение о том, смеяться или нет. Каждый нейрон срабатывает / активируется только тогда, когда его соответствующие критерии (подробнее об этом позже) будут выполнены, как показано ниже.
Конечно, это не совсем так. В действительности, это не просто пара нейронов, которые будут принимать решения. В нашем мозгу имеется массивно параллельная взаимосвязанная сеть из 10¹¹ нейронов (100 миллиардов), и их связи не так просты, как я показал вам выше. Это может выглядеть примерно так:
Теперь органы чувств передают информацию в первый / самый нижний слой нейронов для ее обработки. И выходные данные процессов передаются на следующие уровни иерархическим образом, некоторые нейроны будут срабатывать, а некоторые — нет, и этот процесс будет продолжаться до тех пор, пока не будет получен окончательный ответ — в данном случае, смех.
Эта массивно параллельная сеть также обеспечивает разделение работы. Каждый нейрон срабатывает только тогда, когда его заданные критерии выполнены, то есть нейрон может выполнять определенную роль для определенного стимула, как показано ниже.
Считается, что нейроны расположены иерархически (однако ученые предлагают много надежных альтернатив с экспериментальной поддержкой), и каждый слой имеет свою роль и ответственность. Чтобы обнаружить лицо, мозг может полагаться на всю сеть, а не на один слой.
Теперь, когда мы установили, как работает биологический нейрон, давайте посмотрим, что могли предложить МакКаллох и Питтс.
Примечание: мое понимание того, как работает мозг, очень и очень ограничено. Приведенные выше иллюстрации чрезмерно упрощены.
Маккаллох-Питтс Нейрон
Первая вычислительная модель нейрона была предложена Уорреном Му Каллохом (нейробиологом) и Уолтером Питтсом (логиком) в 1943 году.
Это может быть разделено на 2 части. Первая часть,гпринимает входные данные (ahem dendrite ahem), выполняет агрегирование и на основе агрегированного значения вторую часть,епринимает решение.
Предположим, я хочу предсказать свое собственное решение, смотреть ли случайную футбольную игру или нет по телевизору. Все входные данные являются логическими, то есть {0,1}, а моя выходная переменная также является логическим {0: будет смотреть его, 1: не будет смотреть его}.
- Так,x_1может бытьisPremierLeagueOn(Мне больше нравится Премьер-лига)
- x_2может бытьisItAFriendlyGame(Я склонен меньше заботиться о товарищеских играх)
- x_3может бытьisNotHome(Не могу посмотреть, когда я бегу по делам. Могу ли я?)
- X_4может бытьisManUnitedPlaying(Я большой фанат «МЮ». ГГМУ!) И так далее.
Эти входы могут бытьвозбуждающийилитормозящий, Запрещающие входные данные — это те, которые оказывают максимальное влияние на принятие решений независимо от других входных данных, т.е. еслиx_3равен 1 (не дома), тогда мой вывод всегда будет равен 0, т.е. нейрон никогда не сработает, поэтомуx_3является запрещающим входом. Возбуждающие входы — это НЕ те, которые заставляют нейрон зажигать сами по себе, но они могут запустить его, когда объединены вместе. Формально это то, что происходит:
Мы это видимг(Икс)просто делает сумму входов — простая агрегация А такжететаздесь называется пороговым параметром. Например, если я всегда смотрю игру, когда сумма оказывается равной 2 или более,тетаздесь 2 Это называется пороговой логикой.
Булевы функции с использованием M-P Neuron
До сих пор мы видели, как работает нейрон M-P. Теперь давайте посмотрим, как этот самый нейрон может использоваться для представления нескольких логических функций. Помните, что все наши входные данные являются логическими, а выходные данные также являются булевыми, поэтому по сути нейрон просто пытается выучить булеву функцию. Множество проблем логического решения может быть приведено к этому на основе соответствующих входных переменных — например, будет ли нейрон M-P представлять, продолжать ли читать этот пост, смотреть ли Друзья после прочтения этого поста и т. Д.
M-P Neuron: краткое представление
Это представление просто означает, что для логических входовx_1,x_2а такжеx_3еслиг(Икс)т.е.сумма≥тетаиначе нейрон сработает, он не сработает.
И функция
Нейрон функции AND будет срабатывать только тогда, когда ВСЕ входы включены, т.е.г(Икс)≥ 3 здесь.
ИЛИ Функция
Я считаю, что это говорит само за себя, так как мы знаем, что нейрон функции ИЛИ сработает, если ЛЮБОЙ из входов включен, т.е.г(Икс)≥ 1 здесь.
Функция с запрещающим входом
Теперь это может выглядеть сложно, но на самом деле это не так. Здесь мы имеем запрещающий ввод, т.е.x_2так всякий раз, когдаx_2равно 1, выход будет0. Имея это в виду, мы знаем, чтоx_1 AND! x_2будет выводить 1 только тогда, когдаx_1это 1 иx_20, поэтому очевидно, что пороговый параметр должен быть 1.
Давайте проверим, чтог(Икс)т.е.x_1+x_2будет ≥ 1 только в 3 случаях:
Случай 1: когдаx_1это 1 иx_2это 0
Случай 2: когдаx_1это 1 иx_2это 1
Случай 3: когдаx_10 иx_2это 1
Но как в случае 2, так и в случае 3 мы знаем, что на выходе будет 0, потому чтоx_21 в обоих из них, благодаря ингибированию. И мы также знаем, чтоx_1 AND! x_2выдаст 1 для случая 1 (выше), так что наш параметр порога остается в силе для данной функции.
Функция NOR
Чтобы сработал нейрон NOR, мы хотим, чтобы ВСЕ входы были равны 0, поэтому параметр порогового значения также должен быть 0, и мы принимаем их все как запрещающий ввод.
НЕ функция
Для НЕЙРОНА 1 выводит 0, а 0 выводит 1. Таким образом, мы принимаем вход как запрещающий вход и устанавливаем для параметра порогового значения значение 0. Это работает!
Можно ли представить какую-либо булеву функцию с помощью нейрона M-P? Прежде чем ответить на этот вопрос, давайте разберемся, что делает нейрон M-P геометрически.
Геометрическая интерпретация M-P Neuron
Это лучшая часть поста по моему мнению. Давайте начнем с функции ИЛИ.
ИЛИ Функция
Мы уже обсуждали, что пороговый параметр функции ORтета1, по понятным причинам. Входные данные явно логические, поэтому возможны только 4 комбинации — (0,0), (0,1), (1,0) и (1,1). Теперь строим их на двухмерном графике и используем уравнение агрегации функции OR.
т.е.х_1 + х_2≥1используя который мы можем нарисовать границу решения, как показано на графике ниже. Имейте в виду, это не график реальных чисел.
Мы просто использовали уравнение агрегации, т.е.x_1 + x_2 =1графически показать, что все те входы, выход которых при прохождении через нейрон функции M-P OR находится в положении ON или НАД этой строкой, и все входные точки, лежащие ниже этой линии, будут выводить 0.
Вуаля !! Нейрон M-P только что изучил линейную границу решения! Нейрон M-P разбивает входные наборы на два класса — положительный и отрицательный. Положительные (которые выводят 1) — это те, которые лежат ВКЛ или ВЫШЕ границу решения, а отрицательные (которые выводят 0) — те, которые находятся НИЖЕ за границей решения.
Давайте убедимся в том, что блок M-P делает то же самое для всех булевых функций, посмотрев на другие примеры (если это еще не ясно из математики).
И функция
В этом случае решение граничного уравненияx_1 + x_2 =2, Здесь все входные точки, которые находятся в положении ВКЛ или ВЫШЕ, просто (1,1), выводят 1 при прохождении через нейрон функции И-М. Это подходит! Граница решения работает!
тавтология
Я думаю, вы уже поняли, но что, если у нас более 2 входов?
Функция ИЛИ с 3 входами
Давайте просто обобщим это, посмотрев на блок M-P с 3 входами ИЛИ функции. В этом случае возможными входными данными являются 8 баллов — (0,0,0), (0,0,1), (0,1,0), (1,0,0), (1,0,1) … вы получили точку (ы). Мы можем отобразить их на трехмерном графике, и на этот раз мы рисуем границу решения в 3 измерениях.
«Это птица? Это самолет?
Да, это САМОЛЕТ!
Плоскость, удовлетворяющая решению граничного уравненияx_1 + x_2 + x_3 =1показано ниже:
Не торопитесь и убедитесь сами, посмотрев на приведенный выше график, что все точки, лежащие на или над этой плоскостью (положительное полупространство), приведут к выходу 1 при прохождении через единицу измерения функции ИЛИ и все точки, лежащие под этой плоскостью (отрицательное полупространство) приведет к выводу 0.
Просто вручную кодируя параметр порогового значения, нейрон M-P может удобно представлять логические функции, которые являются линейно разделимыми.
Линейная отделимость (для булевых функций): существует линия (плоскость), такая, что все входы, которые производят 1, лежат на одной стороне линии (плоскости), и все входы, которые производят 0, лежат на другой стороне линии (плоскости) ,
Ограничения M-P Нейрон
- А как насчет небулевых (скажем, реальных) входных данных?
- Всегда ли нам нужно вручную кодировать порог?
- Все ли входы равны? Что если мы хотим придать большее значение некоторым входам?
- Как насчет функций, которые не являются линейно разделимыми? Скажи функцию XOR.
Надеюсь, теперь понятно, почему мы сегодня не используем нейрон M-P. Преодолевая ограничения нейрона M-P, американский психолог Фрэнк Розенблатт предложил классическую модель восприятия, могучийискусственный нейронв 1958 г. Это более обобщенная вычислительная модель, чем нейрон МакКаллоха-Питтса, где веса и пороги могут быть изучены с течением времени.
Ещеперсептрони как он узнает веса и пороги и т.д. в моих будущих постах.
Вывод
В этой статье мы кратко рассмотрели биологические нейроны. Затем мы создали концепцию нейрона MuCulloch-Pitts, первой в истории математической модели биологического нейрона. Мы представили несколько булевых функций, используя нейрон M-P. Мы также попытались получить геометрическое представление о том, что происходит с моделью, используя 3D-графики. В конце концов, мы также создали мотивацию для более обобщенной модели, единственной иискусственный нейрон / персептронмодель.
Спасибо за чтение статьи.
Живи и давай жить другим!
“Можно сказать, что человек,
освоивший методы искусственного интеллекта,
поднимается на качественно новый уровень своего
развития.
Можно сказать, что у него появляется
дар предвидения.
Он может предсказывать будущие
события.
И он знает, как повлиять на эти события.
Он знает, что нужно сделать, чтобы
события развивались в нужном направлении.
Раньше таких людей называли
волшебниками и колдунами.
Поэтому можно почти без преувеличения
сказать, что изучаемый вами элективный курс учит
вас искусству колдовства.
Изучив этот предмет, вы можете
свободно пользоваться основными нейросетевыми
технологиями и даже применять их для достижения
своих личных целей. Как и каким образом? Это
зависит от вашей собственной фантазии и от того,
насколько глубоко вы поняли идеи и освоили
методы искусственного интеллекта”.
Этими словами заканчивается новый
учебно-методический комплекс “Искусственный
интеллект”, готовящийся к выпуску издательством
“БИНОМ” к осени 2009 года. Сегодня мы продолжаем
сокращенную публикацию материалов элективного
курса и планируем в дальнейшем охватить его
целиком с тем расчетом, чтобы читатели нашей
газеты сами смогли овладеть обещанным выше искусством
колдовства.
Понятие об экспертных системах
Данные и знания
Как правило, любая, даже самая
простая, компьютерная программа оперирует не
только с данными, но и со знаниями.
Например, фрагмент программы, предназначенной
для вычисления площади треугольника с
основанием a см и высотой h см, на языке
Pasсal может выглядеть следующим образом:
a := 20;
h := 15;
s := 0.5*a*h;
writeln(‘Площадь треугольника S=’, s, ‘кв.см’);
Первые два оператора представляют
собой данные, а третий оператор — знание. Это
всем известная формула для вычисления площади
треугольника. Она является результатом
интеллектуальной деятельности древних
геометров.
Прежде чем сформулировать определение
знаний, вспомним, что собой представляют данные.
Данные — это отдельные факты,
характеризующие объекты, процессы и явления
предметной области, а также их свойства.
При обработке данные последовательно
трансформируются:
· данные, существующие как результат
измерений и наблюдений;
· данные на материальных носителях
информации — в таблицах, протоколах,
справочниках;
· данные, представленные в виде
диаграмм, графиков, функций;
· данные в компьютере на языке
описания данных;
· базы данных.
Знания основываются на данных, но
представляют собой результат мыслительной
деятельности человека, обобщают его опыт,
полученный в ходе практической деятельности или
научных исследований. Они могут выражать законы
природы и общества, закономерности конкретных
предметных областей.
При обработке на ЭВМ знания
трансформируются аналогично данным:
· знания, существующие в памяти
человека как результат обучения, воспитания,
мышления;
· знания, помещенные на материальных
носителях: в учебниках, инструкциях,
методических пособиях, книгах;
· S знания, описанные на языках
представления знаний и помещенные в компьютер;
· базы знаний.
Итак, для хранения данных в компьютере
используются базы данных, а для хранения знаний
используются базы знаний.
В приведенном выше фрагменте
программы вычисления площади треугольника
знания растворены в самом тексте программы.
Такой вид представления знаний называют процедурным.
Корректировка таких знаний требует изменения
самого текста программы. Поэтому с развитием
искусственного интеллекта все большая часть
знаний стала сосредотачиваться в отдельных
структурах. Такие знания называются декларативными.
Существует множество способов
представления декларативных знаний. Мы
рассмотрим только три наиболее употребляемых
способа:
· продукционные правила;
· фреймы;
· семантические сети.
Способы представления знаний
Продукционные правила
Продукционные правила имеют
следующий вид:
ЕСЛИ “условие”, ТО “действие”.
Например:
ЕСЛИ “холодно”, ТО “надеть шубу”;
ЕСЛИ “идет дождь”, ТО “взять зонтик”.
Продукционные правила — это наиболее
часто используемый способ представления знаний
в современных экспертных системах. Основными
преимуществами таких экспертных систем
являются: высокая модульность, легкость внесения
изменений и дополнений, простота механизма
логического вывода.
Фреймы
В психологии и философии
используется понятие абстрактного образа.
Например, слово “автомобиль” вызывает у
слушающих образ устройства, способного
перемещаться, имеющего четыре колеса, салон для
шофера и пассажиров, двигатель, руль. Считается,
что современный человек широко использует
абстрактные образы для хранения в своей памяти
информации об окружающем мире.
Фрейм — это модель абстрактного
образа, которую программисты используют для
хранения знаний о рассматриваемой предметной
области. Фрейм состоит из имени и отдельных
единиц, называемых слотами. Обычно он имеет
следующую структуру:
Имя фрейма
Имя 1-го слота: значение 1-го слота.
Имя 2-го слота: значение 2-го слота.
. . . . . . . . . . . . . . . . . . . . .
Имя N-го слота: значение N-го
слота.
В качестве значения слота может
выступать имя другого фрейма. Таким образом
фреймы объединяются в сеть. Свойства фреймов
наследуются сверху вниз, т.е. от вышестоящих к
нижестоящим через АКО-связи (начальные буквы
английских слов “a kind of”, что можно перевести как
“это”). Слот с именем АКО указывает на имя фрейма
более высокого уровня иерархии.
Например, на рис. 1 фрейм “Студент”
имеет ссылки на вышестоящие фреймы: “Человек” и
“Млекопитающее”. Поэтому на вопрос “Может ли
студент мыслить?” ответ будет положительным, так
как этим свойством обладает вышестоящий фрейм
“Человек”.
Если одно и то же свойство указывается
в нескольких связанных между собой фреймах, то
приоритет отдается нижестоящему фрейму. Так,
возраст фрейма “Студент” не наследуется из
вышестоящих фреймов.
Основным преимуществом фреймов как
способа представления знаний является
наглядность и гибкость в употреблении. Кроме
того, по мнению многих психологов, фреймовая
структура согласуется с современными
представлениями о хранении информации в памяти
человека.
Семантические сети
В основе этого способа
представления знаний лежит идея о том, что любые
знания можно представить в виде совокупности понятий
(объектов) и отношений (связей). На рис. 2
приведен пример графического изображения сети,
вершины которой представляют собой понятия
предметной области, а связывающие их линии —
отношения между этими понятиями. Сам термин семантическая
означает “смысловая”.
Рис. 2. Семантическая сеть
Основным преимуществом этой модели
является наглядность. Недостаток — сложность
поиска вывода, а также сложность корректировки,
т.е. удаления и дополнения сети новыми знаниями.
Экспертные системы
Назначение
Экспертная система — это
программа, предназначенная для моделирования
деятельности эксперта (специалиста) в какой-либо
предметной области.
Знания, которыми обладают эксперты,
можно разделить на формализуемые, плохо
формализуемые и неформализуемые. Формализуемые
знания излагаются в книгах и руководствах в виде
законов, формул, моделей, алгоритмов.
Формализуемые знания характерны для точных наук,
таких, как математика, физика, химия, астрономия.
Науки, которые принято называть
описательными, обычно оперируют с плохо
формализуемыми знаниями. К таким наукам можно
отнести, например, зоологию, ботанику, экологию,
социологию, педагогику, медицину и др.
Существуют знания, которые не попадают
в книги в связи с их неконкретностью,
субъективностью, приблизительностью. Знания
этого рода являются результатом многолетних
наблюдений, опыта работы, интуиции. Они обычно
представляют собой некие эмпирические и
эвристические приемы и правила. Обычно они
передаются из поколения в поколение в виде
определенных навыков, ноу-хау, секретов ремесла.
Есть также знания, которые вообще не
поддаются формализации. Они не могут быть
выражены ни в математическом виде, ни в терминах
обычного человеческого языка. Такими знаниями
обладают религиозные деятели, экстрасенсы,
контактеры, шаманы.
Класс задач, относящихся к плохо
формализуемым знаниям, значительно шире класса
задач, для которых знания легко поддаются
формализации. Экспертные системы предназначены
для работы именно с плохо формализуемыми
знаниями. Этим объясняется особая популярность
экспертных систем, которые сделали возможным
применение компьютерных технологий в широком
классе предметных областей, характеризующихся
плохо формализуемыми знаниями.
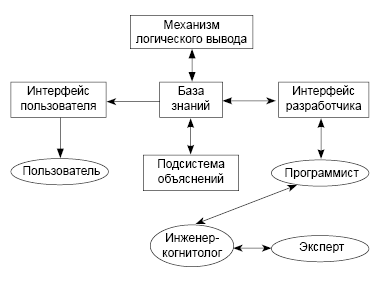
Блок-схема
Типичная блок-схема экспертной
системы представлена на рис. 3.
Рис. 3. Типичная блок-схема
экспертной системы
Обычно в ее состав входят следующие
взаимосвязанные функциональные блоки:
База знаний — ядро экспертной
системы, представляет собой совокупность знаний
предметной области, записанных с помощью
какого-либо способа представления знаний,
например, с помощью продукционных правил,
фреймов, семантических сетей.
Интерфейс разработчика —
программа, предоставляющая инженеру-когнитологу
и программисту возможность создавать базу
знаний в диалоговом режиме; включает системы
вложенных меню, шаблонов языка представления
знаний, подсказок (help-режим) и других сервисных
средств, облегчающих работу с базой знаний.
Интерфейс пользователя — комплекс
программ, реализующих диалог пользователя с
экспертной системой на стадии как ввода
информации, так и получения результатов.
Решатель (синонимы: дедуктивная
машина, блок логического вывода) —
программа, осуществляющая логический вывод
путем моделирования хода рассуждений эксперта
на основании знаний, имеющихся в базе знаний.
Подсистема объяснений —
программа, позволяющая пользователю получать
ответы на вопрос “На основании чего сделано то
или иное заключение?”. Принцип работы этой
программы заключается в том, что она
последовательно выводит на экран компьютера все
правила, которые были задействованы при
получении заключения. В результате, при
прочтении этих правил пользователю становится
понятной логика проделанного экспертной
системой вывода.
В коллектив разработчиков экспертной
системы входят, как минимум, четыре специалиста
(или четыре группы специалистов): эксперт,
инженер-когнитолог, программист, пользователь.
Возглавляет коллектив инженер-когнитолог —
ключевая фигура при разработке экспертных
систем. Обычно это руководитель проекта, в задачу
которого входит организация всего процесса
создания экспертной системы. С одной стороны, он
должен быть специалистом в области
искусственного интеллекта, а с другой — должен
разбираться в предметной области, общаться с
экспертом, извлекая и формализуя его знания,
передавать их программисту, кодирующему и
помещающему их в базу знаний экспертной системы.
Экспертная система работает в двух
режимах — приобретения знаний и решения задач
или проведения консультаций. В режиме
приобретения знаний происходит формирование
базы знаний. В режиме решения задач общение с
экспертной системой осуществляет конечный
пользователь.
Обычно знания, которыми располагает
эксперт, различаются степенью достоверности,
надежности, важности, четкости. В этом случае они
снабжаются некоторыми весовыми коэффициентами,
которые называют коэффициентами доверия (уверенности).
Коэффициенты доверия могут указываться в баллах
или в процентах. Например, если у больного
высокая температура и он кашляет, то с
уверенностью 90% можно утверждать, что он
простужен, и с уверенностью 30% подозревать, что у
него воспаление легких. Коэффициенты доверия
обрабатываются вместе с правилами решателем
экспертной системы, в результате вывод, который
делает экспертная система, тоже снабжается
некоторым коэффициентом доверия, который
показывает, насколько такому выводу можно
доверять. Процесс обработки коэффициентов
доверия решателем осуществляется с помощью
алгоритмов нечеткой логики, которую мы в нашем
курсе касаться не будем.
В процессе опытной эксплуатации
коэффициенты доверия могут подвергаться
корректировке. В этом случае говорят, что
происходит обучение экспертной системы. Процесс
обучения экспертной системы может производиться
автоматически с помощью обучающего алгоритма
либо путем вмешательства инженера-когнитолога,
выполняющего роль учителя.
В табл. 1 приведено несколько
отличительных признаков экспертных систем от
обычных компьютерных программ.
Таблица 1
Отличия экспертных систем
от обычных компьютерных программ
|
Характеристика |
Экспертные |
Традиционные
компьютерные программы |
|
Тип |
Символьная |
Числовая |
|
Метод |
Эвристический |
Алгоритм |
|
Задание |
Неявное |
Точное |
|
Искомое |
Удовлетворительное |
Оптимальное |
|
Управление |
Перемешаны |
Разделены |
|
Знания |
Неточные |
Точные |
|
Модификации |
Частые |
Редкие |
Коротко о главном
Экспертная система — это сложный
программный комплекс, предназначенный для
моделирования деятельности специалиста
(эксперта) в какой-либо предметной области. Ее
главное отличие от обычных программ состоит в
том, что в нее заложены знания эксперта, с помощью
которых она может делать логически обоснованные
выводы.
Вопросы и задания
Не на все из приведенных ниже
вопросов имеются ответы в тексте статьи. Однако
указанные ответы легко найти, например, в
Интернете. Главное — вы знаете, что искать!
1. Дайте определение данных и знаний.
2. Как трансформируются данные и знания
в процессе их обработки?
3. Какие знания называются
процедурными, а какие — декларативными?
4. Перечислите основные преимущества и
недостатки известных вам способов представления
знаний.
5. Какой способ представления знаний
наиболее распространен в современных экспертных
системах?
6. Какой из рассмотренных способов
представления знаний наиболее близок к способу,
которым пользуется мозг человека?
7. Приведите примеры научных областей,
в которых знания хорошо формализованы и где они
плохо поддаются формализации.
8. Дайте определение экспертной
системы.
9. Перечислите функциональные блоки, из
которых состоит типичная экспертная система,
укажите их назначение.
10. Что такое коэффициенты доверия и для
чего они вводятся?
11. Что понимается под обучением
экспертной системы?
12. Укажите несколько отличительных
признаков между экспертной системой и
традиционной компьютерной программой.
13. Из каких специалистов, по вашему
мнению, должен состоять коллектив разработчиков
экспертной системы?
14. Кто был создателем первой
экспертной системы? Для чего она была
предназначена?
НЕЙРОННЫЕ СЕТИ
Персептрон и его развитие
Мозг и компьютер
На самой заре компьютерной эры, в
середине ХХ в., были предложены различные
варианты принципов действия и архитектурного
исполнения электронно-вычислительных машин.
Многие из этих вариантов впоследствии были
отвергнуты и забыты. Наиболее удачной оказалась
архитектура машины фон Неймана, которую имеет
большинство современных компьютеров. Однако
наряду с машиной фон Неймана до наших дней дошла
еще одна схема, которая в последние годы
стремительно развивается и находит применение.
Речь идет о нейрокомпьютерах и нейронных сетях.
Нейронные сети и нейрокомпьютеры —
это одно из направлений компьютерной индустрии,
в основе которого лежит идея создания
искусственных интеллектуальных устройств по
образу и подобию человеческого мозга. Дело в том,
что компьютеры, выполненные по схеме машины фон
Неймана, по своей структуре и свойствам весьма
далеки от нашего естественного компьютера —
человеческого мозга. В подтверждение этому в
табл. 2 приведены признаки, отличающие
человеческий мозг от неймановского компьютера.
Основатели же нейрокибернетики
задались целью создания электронных устройств,
адекватных мозгу не только на функциональном, но
и на структурном уровне. Для этого им пришлось
обратиться за сведениями к биологам. Как же
устроен человеческий мозг?
Известно, что мозг человека состоит из
белого и серого вещества: белое вещество — это
тела нервных клеток, называемых нейронами, а
серое вещество — соединяющие их нервные волокна.
Каждый нейрон состоит из трех частей: тела
клетки, дендритов и аксона (рис. 4).
Дендриты и аксон — это нервные отростки, через
которые нейрон обменивается электрическими
сигналами с другими нейронами. Каждый нейрон
может иметь до 10 000 дендритов и всего лишь один
аксон. Через дендриты нейрон принимает
электрические сигналы, поступающие от других
нейронов по нервным волокнам, как по
проводам. Если сигналов много и они достаточно
интенсивны, то нейрон переходит в возбужденное
состояние и сам вырабатывает электрический
сигнал, который передает в аксон. Аксон на своем
другом конце разветвляется на тысячи нервных
волокон, которые затем соединяются с дендритами
других нейронов. Места соединения нервных
волокон с дендритами называются синапсами.
Как же человеческий мозг запоминает
информацию и как ее обрабатывает? Ответить на
этот вопрос биологи не могли. Но зато они знали,
что общее число нейронов в течение жизни
человека практически не изменяется, т.е. мозг
ребенка и мозг взрослого человека содержат
приблизительно одинаковое количество нейронов.
Примерно одинаковое количество нейронов
содержит мозг ученого, политического деятеля и
спортсмена. Отличие состоит в величинах
электропроводностей синапсов.
Как известно из электротехники,
электропроводность проводника r — это величина,
обратная его электросопротивлению R и
имеющая размерность
1/Ом. Биологи же электропроводности синапсов
назвали силами межнейронных синаптических
связей, и, по их мнению, мозг одного человека
отличается от мозга другого человека прежде
всего силами межнейронных синаптических связей.
На этом основании была высказана гипотеза о том,
что все наши мысли, эмоции, знания, вся
информация, хранящаяся в человеческом мозге,
закодирована в виде огромного количества цифр,
характеризующих силы межнейронных
синаптических связей.
Рис. 4. Нейроны человеческого мозга
А теперь давайте попробуем оценить,
сколько же чисел способен запомнить такой
гипотетический мозг, если принять, что с помощью
одной синаптической связи можно закодировать
одно число.
В человеческом мозге содержится
приблизительно 1011 нейронов. Каждый нейрон
связан с 103…104 другими нейронами.
Таким образом, биологическая нейронная сеть,
составляющая мозг человека, содержит
1014…1015 синапсов. Получается, что
именно такое количество цифр способен хранить
человеческий мозг. Получается, что именно таким
количеством цифр закодированы в нашем мозге все
наши знания, весь жизненный опыт, все мысли и
эмоции, вся информация, которую мы получаем на
протяжении жизни.
Таблица 2
Приведенные выше представления о
строении и функционировании мозга в настоящее
время считаются научно обоснованным фактом. Ни у
кого из ученых не вызывает сомнений, что разум
человека создается огромным количеством
мельчайших нервных клеток — нейронами,
непрерывно исполняющими свой информационный
танец. Что это за “танец”, мы рассмотрим в
следующих разделах.
Биологический и математический
нейроны
Первой работой, заложившей
теоретический фундамент для создания
интеллектуальных устройств, моделирующих
человеческий мозг на самом низшем — структурном
уровне, принято считать опубликованную в 1943 г.
статью Уоррена Мак-Каллока и Вальтера
Питтса “Идеи логических вычислений в нервной
деятельности”. Ее авторы, американские ученые
математики-нейрофизиологи, по праву считающиеся
основателями нейроинформатики, предложили
математическую модель нейрона мозга человека,
назвав ее математическим, или модельным,
нейроном.
Математический нейрон Мак-Каллока –
Питтса изображен на рис. 5 в виде кружочка. Он
имеет несколько входов и один выход, показанные
на рисунке стрелками. Через входы, число которых
обозначим j, математический нейрон принимает входные
сигналы xj, которые суммирует, умножая
каждый входной сигнал на некоторый весовой
коэффициент wj:

(1)
После выполнения операции
суммирования математический нейрон формирует
выходной сигнал y согласно следующему
правилу:
(2)
где — порог чувствительности
нейрона.
Рис. 5. Математический нейрон
Мак-Каллока — Питтса
Таким образом, математический нейрон,
как и его биологический прототип — мозг, может
существовать в двух состояниях — возбужденном и
невозбужденном. Если взвешенная сумма входных
сигналов S меньше некоторой пороговой
величины , то математический нейрон не возбужден
и его выходной сигнал равен нулю. Если же входные
сигналы достаточно интенсивны и их сумма
достигает порога чувствительности, то нейрон
переходит в возбужденное состояние и на его
выходе формируется сигнал y = 1.
Весовые коэффициенты wj:
имеют вполне определенный физический смысл. Они
имитируют электропроводности нервных волокон,
тех самых, которые биологи назвали силами
межнейронных синаптических связей, или синаптическими
весами. Чем эти силы выше, тем больше
вероятность перехода нейрона в возбужденное
состояние.
Ранее мы уже отмечали, что биологи
придают силам синаптических связей очень важное
значение. Считается, что именно с их помощью
человеческий мозг кодирует всю имеющуюся у него
информацию. Как мы увидим далее, в искусственном
мозге — в нейронных сетях и в нейрокомпьютерах,
происходит то же самое. Вся информация в них тоже
кодируется в виде множества цифр,
характеризующих силы межнейронных
синаптических связей wj.
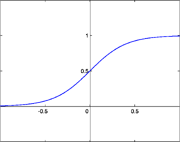
Логическая функция (2) называется активационной
функцией нейрона. Ее графическое изображение,
представленное на рис. 6a, по форме
напоминает ступеньку, поэтому ее называют функцией-ступенькой.
Рис. 6. Пороговые активационные
функции нейрона, заданные формулами: а – (3.2); б –
(3.4); в – (3.5)
Таким образом, математический
нейрон представляет собой пороговый элемент с
несколькими входами и одним выходом. Каждый
математический нейрон имеет свое определенное
значение порога .
С помощью математического нейрона
можно моделировать различные логические
функции, например, функцию логического умножения
“И” (ее также обозначают “AND”), функцию
логического сложения “ИЛИ” (“OR”) и функцию
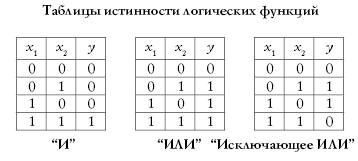
логического отрицания “НЕТ” (“NOT”). Таблицы
истинности этих логических функций приведены в
табл. 3, в которых значение логических функций
“истинно” закодировано единицей, а значение
“ложно” — нулем.
Таблица 3
С помощью этих таблиц и формул (1)–(2)
нетрудно убедиться, что математический нейрон
(см. рис. 7), имеющий два входа с единичными
силами синаптических связей w1 = w2
= 1, моделирует функцию логического умножения
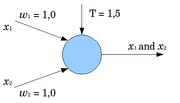
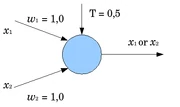
“И” при q = 2. Этот же нейрон
моделирует функцию логического сложения “ИЛИ”
при задании q = 1. Математический
нейрон с одним входом моделирует функцию “НЕТ”
при задании w = -1 и q =
0.
Рис. 7. Математические нейроны,
моделирующие логические функции
В современной литературе иногда
вместо понятия порога чувствительности нейрона q используют
термин нейронное смещение b, которое
отличается от порога q только знаком: b = – q.
Если его добавить к сумме (1):

(3)
то пороговая активационная функция
нейрона примет вид:
(4)
Графическое представление этой
активационной функции приведено на рис. 6б на
с. 21. Еще более симметричный вид, представленный
на рис. 6в, активационная функция нейрона
приобретает при использовании формулы:
(5)
В формуле (3) нейронное смещение b
можно рассматривать как вес w0
некоторого дополнительного входного сигнала x0,
величина которого всегда равна единице:

(6)
Нейрон с дополнительным входом x0
изображен на рис. 8.
Рис. 8. Нейронное смещение b
интерпретируется
как вес дополнительного входа w 0 ,
сигнал которого x 0 всегда равен 1
Коротко о главном
Согласно наиболее распространенным
современным научным представлениям, вся
информация и все знания в человеческом мозге
кодируются и хранятся в виде матрицы сил
межнейронных синаптических связей.
Математический нейрон Мак-Каллока – Питтса —
это математическая модель биологического
нейрона мозга, учитывающая его структуру и
функциональные свойства.
Рекомендации по проведению урока
Как показал опыт, рассказ о строении
мозга и его функционировании обычно
воспринимается учащимися с большим интересом.
Здесь важно завладеть вниманием и не упускать
его до конца урока-лекции. Кроме того, надо
учесть, что материал урока достаточно объемен,
поэтому надо сразу начать лекцию и не сбавлять
темпа изложения материала до самого конца урока,
оставив повторение и закрепление материала на
следующий урок.
Необходимая тишина в классе воцарится
сразу же после того, как вы сообщите, что мозг
каждого человека (включая и слушателей) состоит
из множества нервных клеток — нейронов, число
которых приблизительно равно количеству звезд в
нашей Галактике, что нейроны связаны между собой
нервными волокнами, через которые происходит
обмен электрическими сигналами.
Для лучшего понимания и усвоения
материала школьникам нелишне напомнить сведения
из физики. Написать на доске (а лучше попросить
написать кого-нибудь из школьников) закон Ома I = U
/ R и дать его формулировку: “электрический ток I,
протекающий через проводник, прямо
пропорционален приложенной к его концам
разности потенциалов (напряжению) U и обратно
пропорционален электросопротивлению R этого
проводника”. Вместо электросопротивления
(измеряемого, как известно, в омах) в
электротехнике часто используют обратную ему
величину r = 1 / R, называемую
электропроводностью и измеряемую в сименсах.
Можно спросить школьников: какой из известных им
материалов обладает наиболее высокой
проводимостью, и услышать в ответ — медь,
алюминий (из которых сделана электропроводка в
школе и в их квартирах). Так вот, большинство
ученых склонны считать, что вся хранимая в нашем
мозге информация (все наши мысли, чувства, эмоции,
знания) закодирована с помощью чисел,
характеризующих электропроводности
межнейронных соединений, точнее — с помощью
величин электропроводностей синапсов —
точек контакта между нервными волокнами и дендритами
(см. рис. 4). Именно этот физический факт
заложен в основу математической модели нейрона,
предложенной в 1943 г. американскими
математиками-нейрофизиологами Мак-Каллоком и
Питтсом. Именно этот факт заложен в основу
искусственных нейронных сетей, состоящих из
математических нейронов. Именно этот факт
заложен в основу нейрокомпьютеров, реализующих
искусственные нейронные сети “в железе”. Роль
электропроводностей во всех этих моделях мозга
выполняют весовые коэффициенты, называемые силами
синаптических связей, или синаптическими
весами.
Надо, чтобы школьники и в дальнейшем
помнили приведенную выше физическую трактовку. В
дальнейшем они перейдут от физики к математике и
будут оперировать только математическими и
алгоритмическими понятиями и терминами. И надо
им постоянно напоминать, что за математическими
абстракциями кроется реальная физическая
основа, что в виде сил синаптических связей
(электропроводностей межнейронных связей) в
человеческом мозге хранятся знания. В таком же
виде представляются знания в искусственных
нейронных сетях и нейрокомпьютерах. Именно в
этом состоит принципиальное отличие нейронных
сетей от экспертных систем, где знания хранятся в
явном виде с помощью продукционных правил,
фреймов, семантических сетей.
Давая теоретический материал о
строении мозга, о попытках построения компьютера
по образу и подобию мозга, надо неустанно
повторять, что все это делается не для
развлечения. Это делается не какими-то заумными
учеными ради каких-то отдаленных и нереальных
научных перспектив. Это нужно для того, чтобы
научиться строить компьютерные модели мозга,
чтобы научиться использовать эти
модели-программы для решения практических задач,
которые уже сейчас встречаются и еще не раз будут
встречаться в жизни современных молодых людей.
Нужно говорить о том, что в результате изучения
элективного курса школьники научатся не только
теоретически, но и практически владеть новым
мощным суперсовременным математическим
аппаратом, что они получат и освоят компьютерные
программы, которые смогут применять в жизни для
решения широкого круга практических задач.
В результате изучения материала урока
учащиеся должны иметь представление о
строении мозга и происходящих в нем процессах, знать
математические формулы, которые реализует
математический нейрон, и уметь вычислять его
выход.
Вопросы и задания с ответами и
комментариями
1. Назовите несколько отличительных
признаков в принципах действия современного
компьютера, выполненного по схеме фон Неймана, от
мозга.
Ответ: См. табл. 2.
2. Сколько нейронов имеет человеческий
мозг?
Ответ: В человеческом мозге
содержится приблизительно 1011 нейронов.
3. Сколько дендритов и сколько аксонов
может иметь нейрон? Каково их назначение?
Ответ: Биологический нейрон
может иметь до 10 000 дендритов (через которые он
принимает электрические сигналы от других
нейронов) и один аксон (нервный отросток, через
который нейрон передает свои выходные сигналы
другим нейронам).
4. Сколько нервных волокон, соединяющих
нейроны между собой, имеет человеческий мозг?
Ответ: Если учесть, что мозг
человека содержит приблизительно 1011
нейронов, а каждый нейрон имеет до 10 000
дендритов (через которые он связан с 10 000
других нейронов), то, умножая эти цифры, получим,
что мозг человека содержит до 1015 связей в
виде нервных волокон, соединяющих нейроны между
собой.
5. В каком виде хранится информация в
человеческом мозге?
Ответ: Согласно
распространенным нейрофизиологическим
представлениям, вся информация в человеческом
мозге хранится в виде матрицы сил синаптических
связей.
6. Объясните на языке электротехники
значение термина “сила синаптической связи”. В
каких единицах она измеряется?
Ответ: Сила синаптической
связи — это электропроводность проводника
электрического тока, соединяющего нейроны между
собой. Электропроводность (r)
измеряется в сименсах и представляет собой
величину, обратную электрическому сопротивлению
( R ): r = 1 / R . 1 Сименс = 1 / 1 Ом.
7. Какой объем памяти имеет
человеческий мозг? Сколько чисел он может
запомнить?
Ответ: Человеческий мозг
содержит около 1015 межнейронных
синаптических связей, каждая из которых кодирует
один синаптический вес в виде десятичного числа.
Как известно, для хранения одного десятичного
числа требуется 1 байт информации. Следовательно,
объем памяти человеческого мозга составляет
около 1015 байт. Именно столько цифр он может
запомнить. Естественно, что это всего лишь
теоретический результат, полученный на
основании гипотезы о том, что информация в
человеческом мозге кодируется в виде сил
синаптических связей.
8. Сколько входов и сколько выходов
имеет биологический нейрон?
Ответ: Биологический нейрон
имеет один выход (аксон) и до 10 000 входов
(дендритов).
9. Сколько входов и сколько выходов
может иметь математический нейрон Мак-Каллока –
Питтса?
Ответ: Математический нейрон
Мак-Каллока – Питтса имеет один выход и любое
количество входов.
10. Напишите формулы, с помощью которых
происходит преобразование сигналов в
математическом нейроне Мак-Каллока – Питтса.
Ответ: Работа математического
нейрона Мак-Каллока – Питтса описывается
формулами (1)–(2).
11. Нарисуйте графическое изображение
активационной функции математического нейрона
Мак-Каллока – Питтса.
Ответ: См. рис. 6а.
12. Нарисуйте математические нейроны,
реализующие логические функции “И”, “ИЛИ”,
“НЕТ”, и приведите соответствующие им значения
сил синаптических связей и порогов.
Ответ: См. рис. 7.
13. Нарисуйте математический нейрон и
напишите формулы, по которым он работает, с
использованием понятия смещения вместо порога.
Какой вид при этом имеет активационная функция
нейрона?
Ответ: См. рис. 8; формулы
(3.3)–(3.6); рис. 6б, в [1].
14. Чем весовые коэффициенты отличаются
от синаптических весов и от сил синаптических
связей?
Ответ: Ничем. Это все синонимы.
15. Чем нейронное смещение b
отличается от порога чувствительности q?
Ответ: Они различаются только
знаком: b = -q.
Лабораторная работа № 1:
“Математический нейрон”
Первая лабораторная работа
посвящена изучению математического нейрона
Мак-Каллока – Питтса. Перед включением
компьютеров школьникам рекомендуется напомнить
содержание предыдущего урока — нарисовать на
доске изображение математического нейрона (рис.
4) и написать формулы (1) и (2), по которым он
работает. Согласно этим формулам, если
взвешенная сумма входных сигналов меньше
некоторой пороговой величины , то выходной
сигнал равен нулю. Если же входные сигналы
достаточно интенсивны и их сумма достигает
порога чувствительности, то на выходе нейрона
формируется сигнал . Зависимость (2) изображают
графически (см. рис. 6а) и называют
активационной функцией нейрона.
Напомните школьникам, что с помощью
математического нейрона можно моделировать
различные логические функции. Напомните им, что
собой представляют логические функции “И”,
“ИЛИ” и “Исключающее ИЛИ”, и нарисуйте (или
попросите нарисовать школьников) на доске
таблицы истинности этих функций:
Лабораторная работа состоит в
следующем: школьникам предлагается попробовать
вручную подобрать по два варианта параметров
нейрона (величину порога и синаптические силы)
так, чтобы он моделировал все эти логические
функции. На предыдущем уроке некоторые варианты
решения этой задачи уже приводились. Например,
сообщалось, что при w1 = w2 = 1, q = 2, нейрон реализует функцию
логического умножения “И”, а при задании q = 1этот же нейрон реализует функцию
логического сложения “ИЛИ”. Можно подсказать
эти значения параметров нейрона школьникам или
дать им возможность посмотреть тетрадки или
учебник. Однако лучше устроить соревнование —
кто первый справится со всеми заданиями
лабораторной работы, тот будет отмечен
положительной оценкой.
Работа проходит в виде азартной игры,
правила которой школьники быстро осваивают сами.
Преподавателю рекомендуется, не делая долгих
вступлений, усадить школьников за компьютеры и
запустить первую лабораторную работу.
Содержимое лабораторных работ рекомендуется
предварительно скачать на школьные компьютеры с
сайта http://www.LbAI.ru.
Школьникам надо сказать, что они
должны выполнять задания, появляющиеся в
“Протоколе выполнения”. Между компьютерами и
школьниками завязывается диалог, который
протоколируется и впоследствии может быть
проверен преподавателем.
Школьникам преподносится
своеобразный “сюрприз”: если с двумя первыми
заданиями (моделирование функций “И” и “ИЛИ”)
школьники с нескольких попыток справляются, то
последнее задание (моделирование функции
“Исключающее ИЛИ”) они не могут выполнить в
принципе, сколько бы попыток ни делали.
Здесь авторы лабораторного практикума
воспользовались известным историческим фактом,
произошедшим в 50-е гг. XX в. Многие ученые тогда
пытались применять нейронные сети для решения
таких задач, как прогнозирование погоды и курсов
валют, постановка медицинских диагнозов и др.
Иногда им это удавалось, но чаще они терпели
неудачу. Задачи внешне мало чем различались
между собой, однако с одними из них нейросети
успешно справлялись, а с другими — нет. Объяснить
причины неудач никто не мог, и исследователи
продолжали свои попытки, расходуя массу времени
и финансовых ресурсов. И только более глубокие
исследования, выполненные американскими
математиками М.Минским и С.Пейпертом
(которые затем изучаются на следующих уроках),
помогли разобраться в причинах парадоксальных
неудач.
Таким образом, школьники на
собственном опыте как бы повторяют историю
развития нейроинформатики.
С помощью нейрона Мак-Каллока – Питтса они с
успехом решают задачи моделирования логических
функций “И” и “ИЛИ”, но никак не могут решить
задачу моделирования функции “Исключающее
ИЛИ”, хотя внешне эти функции мало чем
различаются между собой.
Разочаровавшихся школьников следует
успокоить, сообщив им, что не одни они попались в
ловушку. В середине XX в. решением линейно
неразделимых задач, типа проблемы “Исключающего
ИЛИ”, долго и безуспешно занимались многие
ученые, а бизнесмены и американское
правительство вкладывали в эти исследования
немалые финансовые средства.
По мнению авторов лабораторного
практикума, этот неудачный опыт позволяет
учащимся глубоко прочувствовать проблему,
задуматься над ней и в дальнейшем избегать
подобных ошибок при практическом применении
нейросетевых технологий.
Ниже на рисунке приведено рабочее окно
1-й лабораторной работы. Вверху в виде
развернутой книги помещена кнопка вызова
теоретического материала, однако лучше, если
школьники его прочитают после того, как попотеют
над выполнением заданий, появляющихся в
“Протоколе выполнения”. Им надо предоставить
возможность осваивать программный интерфейс так
же, как они осваивают большинство своих
программ-игрушек. Обычно они ленятся читать
инструкции, а осваивают новые игры путем
нажимания кнопок наугад. Так что здесь мы
рекомендуем преподавателю не мешать школьникам
заниматься их любимым делом. Пусть они читают
задания и пытаются их выполнить, наблюдая за
комментариями, появляющимися в “Протоколе
выполнения”.
Рабочее окно лабораторной работы № 1
В нижней части рабочего окна приведена
графическая интерпретация работы нейрона, с
помощью которой можно догадаться о причинах
неудач, постигающих школьников. Но это под силу
только особо одаренным детям, которые
встречаются крайне редко. На вопрос школьников
об этих графиках можно ответить, что их суть
будет объяснена на последующих уроках.
Школьников, которые первыми
догадались прочитать теоретический материал и
поняли, что проблему “Исключающего ИЛИ” с
помощью одного математического нейрона решить
невозможно, желательно отметить положительными
оценками. Выполнившим лабораторную работу № 1
раньше, чем закончится урок, можно предложить
начать выполнение лабораторной работы № 2.
В конце урока ученикам рекомендуется
задать вопрос, почему же невозможно с помощью
математического нейрона моделировать функцию
“Исключающее ИЛИ”, в то время как с
моделированием других, внешне мало чем
отличающихся функций (“И” и “ИЛИ”) проблем не
возникало. Ответ на этот очень сложный вопрос
школьники (и учителя тоже) получат на следующих
уроках, а пока и школьникам, и учителям
предлагается просто задуматься над этим
парадоксом.
В результате выполнения лабораторной работы №
1 учащиеся должны понимать принцип действия
математического нейрона, уметь подбирать
синапрические веса и пороги нейронов,
моделирующих логические функции “И” и “ИЛИ”, знать,
что не все логические функции удается
моделировать с помощью математического нейрона, задуматься
над объяснением этого парадокса и подумать
над его преодолением.

Схема искусственного нейрона
1.Нейроны, выходные сигналы которых поступают на вход данному
2.Сумматор входных сигналов
3.Вычислитель передаточной функции
4.Нейроны, на входы которых подаётся выходной сигнал данного
5.
Иску́сственный нейро́н (Математический нейрон Маккалока — Питтса, Формальный нейрон[1]) — узел искусственной нейронной сети, являющийся упрощённой моделью естественного нейрона.
Математически, искусственный нейрон обычно представляют как некоторую нелинейную функцию от единственного аргумента — линейной комбинации всех входных сигналов. Данную функцию называют функцией активации[2] или функцией срабатывания, передаточной функцией. Полученный результат посылается на единственный выход. Такие искусственные нейроны объединяют в сети — соединяют выходы одних нейронов с входами других. Искуственные нейроны и сети являются основными элементами идеального нейрокомпьютера.[3]
Биологический прототип
Биологический нейрон состоит из тела диаметром от 3 до 100 мкм, содержащего ядро (с большим количеством ядерных пор) и другие органеллы (в том числе сильно развитый шероховатый ЭПР с активными рибосомами, аппарат Гольджи), и отростков. Выделяют два вида отростков. (Аксон обычно — длинный отросток, приспособленный для проведения возбуждения от тела нейрона. Дендриты — как правило, короткие и сильно разветвлённые отростки, служащие главным местом образования влияющих на нейрон возбуждающих и тормозных синапсов (разные нейроны имеют различное соотношение длины аксона и дендритов). Нейрон может иметь несколько дендритов и обычно только один аксон. Один нейрон может иметь связи с 20-ю тысячами других нейронов. Кора головного мозга человека содержит 10—20 миллиардов нейронов.
История развития
Математическая модель искусственного нейрона была предложена У. Маккалоком и В. Питтсом вместе с моделью сети, состоящей из этих нейронов. Авторы показали, что сеть на таких элементах может выполнять числовые и логические операции[4]. Практически сеть была реализована Фрэнком Розенблаттом в 1958 году как компьютерная программа, а в последствии как электронное устройство — перцептрон. Первоначально нейрон мог оперировать только с сигналами логического нуля и логической единицы[5], поскольку был построен на основе биологического прототипа, который может пребывать только в двух состояниях — возбужденном или невозбужденном. Развитие нейронных сетей показало, что для расширения области их применения необходимо, чтобы нейрон мог работать не только с бинарными, но и с непрерывными (аналоговыми) сигналами. Такое обобщение модели нейрона было сделано Уидроу и Хоффом[6], которые предложили в качестве функции срабатывания нейрона использовать логистическую кривую.
Связи между искусственными нейронами
Связи, по которым выходные сигналы одних нейронов поступают на входы других, часто называют синапсами по аналогии со связями между биологическими нейронами. Каждая связь характеризуется своим весом. Связи с положительным весом называются возбуждающими, а с отрицательным — тормозящими[7]. Нейрон имеет один выход, часто называемый аксоном по аналогии с биологическим прототипом. С единственного выхода нейрона сигнал может поступать на произвольное число входов других нейронов.
Математическая модель
Математически нейрон представляет собой взвешенный сумматор, единственный выход которого определяется через его входы и матрицу весов следующим образом:
Здесь 

![{displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)

Передаточная функция нейрона
Передаточная функция определяет зависимость сигнала на выходе нейрона от взвешенной суммы сигналов на его входах. В большинстве случаев она является монотонно возрастающей и имеет область значений ![{displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)
![{displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
Классификация нейронов
В основном, нейроны классифицируют на основе их положения в топологии сети. Разделяют:
- Входные нейроны — принимают исходный вектор, кодирующий входной сигнал. Как правило, эти нейроны не выполняют вычислительных операций, а просто передают полученный входной сигнал на выход, возможно, усилив или ослабив его;
- Выходные нейроны — представляют из себя выходы сети. В выходных нейронах могут производиться какие-либо вычислительные операции;
- Промежуточные нейроны — выполняют основные вычислительные операции[9].
Основные типы передаточных функций
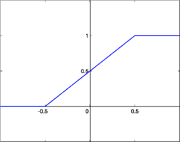
Линейная функция активации с насыщением
Линейная передаточная функция
Сигнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе.
В искусственных нейронных сетях со слоистой структурой нейроны с передаточными функциями такого типа, как правило, составляют входной слой. Кроме простой линейной функции могут быть использованы её модификации. Например полулинейная функция (если ее аргумент меньше нуля, то она равна нулю, а в остальных случаях, ведет себя как линейная) или шаговая (линейная функция с насыщением), которую можно выразить формулой[10]:
При этом возможен сдвиг функции по обеим осям (как изображено на рисунке).
Недостатками шаговой и полулинейной активационных функций относительно линейной можно назвать то, что они не являются дифференцируемыми на всей числовой оси, а значит не могут быть использованы при обучении по некоторым алгоритмам.
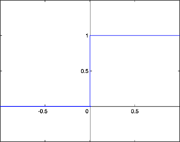
Пороговая функция активации
Пороговая передаточная функция
Представляет собой перепад. До тех пор пока взвешенный сигнал на входе нейрона не достигает некоторого уровня 
Здесь 

Сигмоидальная функция активации
Сигмоидальная передаточная функция
Один из самых часто используемых, на данный момент, типов передаточных функций. Введение функций сигмоидального типа было обусловлено ограниченностью нейронных сетей с пороговой функцией активации нейронов — при такой функции активации любой из выходов сети равен либо нулю, либо единице, что ограничивает использование сетей не в задачах классификации. Использование сигмоидальных функций позволило перейти от бинарных выходов нейрона к аналоговым[12]. Функции передачи такого типа, как правило, присущи нейронам, находящимся во внутренних слоях нейронной сети.
Логистическая функция
Математически эту функцию можно выразить так:
Здесь A — это параметр функции, определяющий её крутизну. Когда A стремится к бесконечности, функция вырождается в пороговую. При 
То, что производная этой функции может быть выражена через её значение облегчает использование этой функции при обучении сети по алгоритму обратного распространения[13]. Особенностью нейронов с такой передаточной характеристикой является то, что они усиливают сильные сигналы существенно меньше, чем слабые, поскольку области сильных сигналов соответствуют пологим участкам характеристики. Это позволяет предотвратить насыщение от больших сигналов[14].
Гиперболический тангенс
Использование функции гиперболического тангенса
отличается от рассмотренной выше логистической кривой тем, что его область значений лежит в интервале (-1;1).
Т.к. верно соотношение
,
то оба графика отличаются лишь масштабом осей.
Производная гиперболического тангенса, разумеется, тоже выражается квадратичной функцией значения; свойство противостоять насыщению имеет место точно также.
Радиально-базисная функция передачи[15]
Этот тип функций принимает в качестве аргумента расстояние между входным вектором и некоторым наперед заданным центром активационной функции. Значение этой функции тем выше, чем ближе входной вектор к центру[16]. В качестве радиально-базисной можно, например, использовать функцию Гаусса:
Здесь 




Здесь 

В реальных сетях активационная функция этих нейронов может отражать распределение вероятности какой-либо случайной величины, либо обозначать какие-либо эвристические зависимости между величинами.
Другие функции передачи
Перечисленные выше функции составляют лишь часть от множества передаточных функций, используемых на данный момент. В число других передаточных функций входят такие как[10]:
Схема нейрона, настроенного на моделирование логического «И» Схема нейрона, настроенного на моделирование логического «ИЛИ» Схема нейрона, настроенного на моделирование логического «НЕ»
Моделирование формальных логических функций
Нейрон с пороговой передаточной функцией может моделировать различные логические функции. Изображения иллюстрируют, каким образом можно, задав веса входных сигналов и порог чувствительности, заставить нейрон выполнять конъюнкцию(логическое «И») и дизъюнкцию(логическое «ИЛИ») над входными сигналами, а также логическое отрицание входного сигнала[19]. Этих трех операций достаточно, чтобы смоделировать абсолютно любую логическую функцию любого числа аргументов.
Различия между биологическим и искусственным нейроном
Нейронные сети, построенные на искусственных нейронах, обнаруживают некоторые признаки, которые позволяют сделать предположение о сходстве их структуры со структурой мозга живых организмов. Тем не менее, даже на низшем уровне искусственных нейронов существуют существенные различия. Например, искусственный нейрон является безынерционной системой, то есть сигнал на выходе появляется одновременно с появлением сигналов на входе, что совсем нехарактерно для биологического нейрона.
Примечания
- ↑ Людмила Георгиевна Комарцова, Александр Викторович Максимов — Нейрокомпьютеры
- ↑ По аналогии с нейронами активации
- ↑ Миркес Е. М., pca.narod.ru/MirkesNeurocomputer.htm Нейрокомпьютер. Проект стандарта. — Новосибирск: Наука, 1999. — 337 с. ISBN 5-02-031409-9
- ↑ В книге McCulloch W.S., Pitts W. A logical Clculus of Ideas Immanent in Nervous Activity — Bull. Mathematical Biophysics, 1943
- ↑ 5,0 5,1 5,2 Л. Н. Ясницкий — Введение в искусственный интеллект — с.29
- ↑ В работе Widrow B., Hoff M.E. Adaptive switching circuits. 1960 IRE WESTCON Conferencion Record. — New York, 1960
- ↑ В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.11
- ↑ 8,0 8,1 В. А. Терехов — Нейросетевые системы управления — с.12-13
- ↑ В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.14
- ↑ 10,0 10,1 В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.12 Ошибка цитирования Неверный тег
<ref>: название «Kruglov12» определено несколько раз для различного содержимого - ↑ Очень часто в литературе можно встретить название персептрон
- ↑ Л. Н. Ясницкий — Введение в искусственный интеллект — с.34
- ↑ CIT forum — Нейрокомпьютеры — архитектура и реализация
- ↑ В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.13
- ↑ В литературе часто встречается сокращение RBF, порождённое английским названием
- ↑ Л. Н. Ясницкий — Введение в искусственный интеллект — с.77
- ↑ В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.349
- ↑ В. В. Круглов, В. В. Борисов — Искусственные нейронные сети. Теория и практика — с.348
- ↑ Л. Н. Ясницкий — Введение в искусственный интеллект — c.30
Ссылки
- Лаборатория анализа данных BaseGroup
Литература
- В. А. Терехов, Д. В. Ефимов, И. Ю. Тюкин Нейросетевые системы управления. — 1-е. — Высшая школа, 2002. — С. 184. — ISBN 5-06-004094-1
- Круглов Владимир Васильевич, Борисов Вадим Владимирович Искусственные нейронные сети. Теория и практика. — 1-е. — М.: Горячая линия — Телеком, 2001. — С. 382. — ISBN 5-93517-031-О
- Роберт Каллан Основные концепции нейронных сетей = The Essence of Neural Networks First Edition. — 1-е. — «Вильямс», 2001. — С. 288. — ISBN 5-8459-0210-X
- Л.Н. Ясницкий Введение в искусственный интеллект. — 1-е. — Издательский центр «Академия», 2005. — С. 176. — ISBN 5-7695-1958-4
- Людмила Георгиевна Комарцова, Александр Викторович Максимов Нейрокомпьютеры. — 1-е. — Изд-во МГТУ им. Н.Э. Баумана, 2002. — С. 320. — ISBN 5-7038-1908-3
Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Искусственный нейрон. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

Контрольные вопросы и задания 41
предметную область, наблюдения за работой эксперта, за процессом принятия решений. К пассивным методам относится также прослушивание лекций, читаемых экспертом, изучение его инструкций и протоколов «мыслей вслух» — попыток объяснить принимаемые им решения.
Активные методы отличаются широким разнообразием ассортимента. Это анкетирование, интервью, свободный диалог, экспертные игры, дискуссии за круглым столом с участием нескольких экспертов, мозговой штурм. В результате инженер по знаниям формирует концептуальную структуру предметной области — модель предметной области, включающую описание ее объектов и связей между ними. Концептуальную структуру изображают в виде графов, фреймов либо описывают словами. Затем формируется функциональная структура предметной области — модель рассуждений эксперта и процесса принятия решений. Она представляется в виде таблицы, графа или в виде предложений естественного языка. Здесь могут присутствовать математические формулы, отражающие внутренние закономерности предметной области, а также продукционные правила, имеющие эвристическую природу, а потому снабженные коэффициентами уверенности.
Процесс проектирования базы знаний заканчивается ее формализацией и программной реализацией.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1.Приведите примеры предметных областей, в которых знания 1) легко поддаются формализации, 1) плохо поддаются формализации,
1)не могут быть формализованы.
5.Дайте определение и сформулируйте назначение экспертной системы.
6.Приведите примеры известных вам экспертных систем.
7.Что такое оболочка экспертной системы?
8.Какой, по вашему мнению, должен быть коллектив разработчиков экспертной системы?
9.Перечислите и охарактеризуйте стадии и этапы разработки экспертных систем.
10.Назовите отличительные признаки экспертной системы.
11.Назовите и охарактеризуйте основные стратегии получения знаний.
12.Почему задачу извлечения знаний называют «узким горлышком»
впроектировании экспертных систем? Какие идеи вы можете предложить для устранения этой ситуации?

Глава 4
ПОНЯТИЕ О КЛАССИЧЕСКОЙ НЕЙРОННОЙ СЕТИ
4.1.МОЗГ И КОМПЬЮТЕР
Нейронные сети и нейрокомпьютеры — это одно из направлений компьютерной индустрии, в основе которого лежит идея создания искусственных интеллектуальных устройств «по образу и подобию» человеческого мозга. Дело в том, что большинство современных компьютеров имеют архитектуру фон Неймана. Согласно этой архитектуре, они имеют центральный процессор, запоминающее устройство, устройства ввода, устройства вывода, устройства хранения информации. По своей структуре и свойствам эти компьютеры весьма далеки от нашего естественного компьютера — человеческого мозга. В подтверждение этому в табл. 4.1 приведены признаки, отличающие человеческий мозг от неймановского компьютера.
Таблица 4.1
Сопоставление принципов построения и свойств современного компьютера (машины фон Неймана) и человеческого мозга
|
Признаки |
Компьютер |
Человеческий мозг |
|
Сложный |
Простой |
|
|
Процессор |
Высокоскоростной |
Низкоскоростной |
|
Один или несколько |
Большое количество |
|
|
Отделена от процессора |
Интегрирована в процес- |
|
|
Память |
сор |
|
|
Локализована |
Распределенная |
|
|
Адресация не по |
Адресация по содержанию |
|
|
содержанию |
||
|
Централизованные |
Распределенные |
|
|
Вычисления |
Последовательные |
Параллельные |
|
Хранимые программы |
Самообучение |
|
|
Надежность |
Высокая уязвимость |
Живучесть |
|
Среда функци- |
Строго определенная |
Плохо определенная |
|
онирования |
||
|
Строго ограниченная |
Без ограничений |
|

4.1. Мозг и компьютер 43
Рис. 4.1. Нейроны человеческого мозга
Основатели же нейрокибернетики1) задались целью создать электронные устройства, адекватные мозгу не только на функциональном, но и на структурном уровне. Для этого им пришлось обратиться за сведениями к биологам. Как же устроен человеческий мозг?
Известно, что мозг человека состоит из белого и серого вещества:
|
белое вещество — это тела нервных |
клеток, называемых |
нейронами, |
|
а серое вещество — соединяющие |
их нервные волокна. |
Каждый |
нейрон состоит из трех частей: тела клетки, дендритов и аксона (рис. 4.1). Дендриты и аксон — это нервные отростки, через которые нейрон обменивается электрическими сигналами с другими нейронами. Каждый нейрон может иметь до 10 000 дендритов и всего лишь один аксон. Через дендриты нейрон принимает электрические сигналы, поступающие от других нейронов по нервным волокнам, как по проводам. Если сигналов много и они достаточно интенсивны, то нейрон переходит в возбужденное состояние и сам вырабатывает электрический сигнал, который передает в аксон. Аксон на своем другом конце разветвляется на тысячи нервных волокон, которые затем соединяются с дендритами других нейронов. Места соединения нервных волокон с дендритами называются синапсами.
Как же человеческий мозг запоминает информацию и как ее обрабатывает? Ответить на этот вопрос биологи не могли. Но зато они знали, что общее число нейронов в течение жизни человека практически не изменяется. Это значит, что мозг ребенка и мозг взрослого человека содержат приблизительно одинаковое количество
1)Эту стратегию создания интеллектуальных систем в гл. 1 книги мы также называли низкоуровневой, или восходящей.

44 Глава 4. Понятие о классической нейронной сети
нейронов. Примерно одинаковое количество нейронов содержит мозг ученого, политического деятеля, солдата, спортсмена. Отличие состоит в величинах электропроводностей синапсов.
Как известно из электротехники, электропроводность проводника ρ— это величина, обратная его электрическому сопротивлению R, т. е. ρ = R1 . Сопротивление R входит в закон Ома, U = IR, как
коэффициент пропорциональности между приложенной к концам проводника разности потенциалов U и силой тока I, возникающего в проводнике под действием этой разности потенциалов. Чем выше электропроводность проводника ρ, тем лучше его способность
проводить электрический ток.
Биологи электропроводности синапсов называют силами межнейронных синаптических связей. По их мнению, мозг одного человека отличается от мозга другого человека прежде всего величинами сил межнейронных синаптических связей. На этом основании была высказана гипотеза о том, что все наши мысли, эмоции, знания, вся информация, хранящаяся в человеческом мозге, закодирована в виде огромного количества чисел, характеризующих силы межнейронных синаптических связей.
А теперь попробуем оценить, сколько же чисел способен запомнить такой гипотетический мозг, если принять, что с помощью одной синаптической связи можно закодировать одно число.
В человеческом мозге содержится приблизительно 1011 нейронов. Каждый нейрон связан с 103…104 другими нейронами. Таким образом, биологическая нейронная сеть, составляющая мозг человека, содержит 1014…1015 синапсов. Получается, что именно такое количество чисел способен хранить человеческий мозг и что именно таким количеством чисел закодированы в нашем мозге все наши знания, весь жизненный опыт, все мысли и эмоции, вся информация, которую мы получаем на протяжении жизни.
Приведенные выше представления о строении и функционировании мозга в настоящее время считаются научно обоснованным фактом. Ни у кого из ученых не вызывает сомнений, что разум человека создается огромным количеством мельчайших нервных клеток — нейронами, непрерывно исполняющими свой «информационный танец». Что это за «танец», мы рассмотрим в следующих параграфах.
4.2.МАТЕМАТИЧЕСКИЙ НЕЙРОН МАК-КАЛЛОКА—ПИТТСА
Первой работой, которая заложила теоретический фундамент для создания интеллектуальных устройств, моделирующих человеческий мозг на самом низшем — структурном — уровне, принято считать

|
4.2. |
Математический нейрон Мак-Каллока—Питтса 45 |
|||
|
опубликованную в |
1943 г. статью Уоррена Мак- |
|||
|
Каллока и Вальтера Питтса «Идеи логических вы- |
||||
|
числений в нервной деятельности» [100]. Ее авторы, |
||||
|
американские ученые математики-нейрофизиологи, |
||||
|
по праву считаются основателями нейроинформати- |
||||
|
ки. Они предложили математическую модель нейрона |
||||
|
мозга человека, назвав ее математическим или |
||||
|
модельным нейроном. |
||||
|
Рис. 4.2. Мате- |
||||
|
У. Мак-Каллок и В. Питтс предложили изображать |
||||
|
нейрон в виде кружочка со стрелочками, как показано |
матический ней- |
|||
|
на рис. 4.2. Стрелки означают входы и выход нейрона. |
рон Мак-Калло- |
|||
|
Через входы математический нейрон принимает |
ка—Питтса |
|||
|
входные сигналы x1, x2, . . ., xj, . . ., xJ и суммирует их, |
умножая |
|
|
каждый входной сигнал на некоторый весовой коэффициент wj: |
||
|
J |
||
|
X |
||
|
S = |
wjxj. |
(4.1) |
j=1
После выполнения операции суммирования математический нейрон формирует выходной сигнал y согласно следующему правилу:
|
1, |
если S > θ; |
|
|
y = 0, |
если S < θ, |
(4.2) |
где θ— порог чувствительности нейрона.
Таким образом, математический нейрон, как и его биологический прототип — нейрон мозга, может существовать в двух состояниях — возбужденном и невозбужденном. Если взвешенная сумма входных сигналов S меньше пороговой величины θ, то математический
нейрон не возбужден и его выходной сигнал равен нулю. Если же входные сигналы достаточно интенсивны и их сумма достигает порога чувствительности θ, то нейрон переходит в возбужденное состояние
и на его выходе формируется сигнал y = 1.
Весовые коэффициенты wj имеют определенный физический смысл. Они имитируют электропроводности нервных волокон, тех самых, которые биологи называют силами межнейронных синаптических связей или синаптическими весами. Чем эти силы больше, тем большей величины сигналы попадают в нейрон и тем выше вероятность его перехода в возбужденное состояние.
Ранее мы уже отмечали, что биологи придают силам синаптических связей очень важное значение. Многие из них полагают, что именно с их помощью человеческий мозг кодирует всю имеющуюся у него информацию. Как мы увидим далее, в искусственном мозге — в нейронных сетях и в нейрокомпьютерах — происходит то же самое. Вся информация в них тоже кодируется в виде множества чисел, характеризующих силы межнейронных синаптических связей wj.

46 Глава 4. Понятие о классической нейронной сети
Рис. 4.3. Пороговые активационные функции нейрона, заданные формулами: а — (4.2); б — (4.4); в — (4.5)
Логическая функция (4.2) называется активационной функцией нейрона. Ее графическое изображение, представленное на рис. 4.3, a, по форме напоминает ступеньку, поэтому ее называют функциейступенькой.
Таким образом, математический нейрон представляет собой пороговый элемент с несколькими входами и одним выходом. Каждый математический нейрон имеет свое определенное значение порога чувствительности θ.
Авторы математического нейрона У. Мак-Каллок и В. Питтс в своей статье [100] также показали, что с помощью математического нейрона можно моделировать различные логические функции, например функцию логического умножения «И» (ее также обозначают «AND»), функцию логического сложения «ИЛИ» («OR») и функцию логического отрицания «НЕТ» («NOT»). Таблицы истинности этих логических функций приведены в табл. 4.2, в которых значение логических функций «истинно» закодировано единицей, а значение «ложно» — нулем.
С помощью этих таблиц и формул (4.1)–(4.2) нетрудно убедиться, что математический нейрон (рис. 4.4), имеющий два входа с единичными силами синаптических связей w1 = w2 = 1, моделирует функцию логического умножения «И» при θ = 2, Этот же нейрон моделирует функцию логического сложения «ИЛИ» при задании θ = 1. Матема-
Таблица 4.2
Таблицы истинности логических функций
|
x1 |
x2 |
y |
x1 |
x2 |
y |
x |
y |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
||
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
||
|
1 |
0 |
0 |
1 |
0 |
1 |
«НЕТ» |
|||
|
1 |
1 |
1 |
1 |
1 |
1 |
||||

4.2. Математический нейрон Мак-Каллока—Питтса 47
Рис. 4.4. Математические нейроны, моделирующие логические функции
тический нейрон с одним входом моделирует функцию «НЕТ» при задании w = −1 и θ = 0.
В современной литературе иногда вместо понятия порога чувствительности нейрона θ используют термин нейронное смещение b,
|
которое отличается от θ только |
знаком: b = −θ. Если его |
добавить |
|
к сумме (4.1): |
||
|
J |
||
|
X |
||
|
S = |
wjxj + b, |
(4.3) |
j=1
то пороговая активационная функция нейрона примет вид:
|
1, |
если S > 0; |
|
|
y = 0, |
если S < 0, |
(4.4) |
Графическое представление этой активационной функции приведено на рис. 4.3, б. Еще более симметричный вид, представленный на рис. 4.3, в, активационная функция нейрона приобретает при использовании формулы:
|
1, |
если S > 0; |
||||||
|
y = −1, |
если S < 0, |
(4.5) |
|||||
|
В формуле (4.3) нейронное смещение b мож- |
|||||||
|
Рис. 4.5. Нейронное |
|||||||
|
но рассматривать как вес w0 некоторого до- |
|||||||
|
полнительного входного сигнала x0, величина |
смещение b интерпрети- |
||||||
|
которого всегда равна единице: |
руется как вес дополни- |
||||||
|
тельного входа с силой |
|||||||
|
J |
J |
||||||
|
синаптической связи w0, |
|||||||
|
S = |
wjxj + w0x0 = |
wjxj. |
(4.6) |
||||
|
сигнал которого x0 все- |
|||||||
|
X |
X |
гда равен единице |
|||||
|
j=1 |
j=0 |
Нейрон с дополнительным входом x0 изображен на рис. 4.5.
Подводя итог изложенному, еще раз отметим, что, согласно наиболее распространенным современным научным представлениям, вся

48 Глава 4. Понятие о классической нейронной сети
информация и все знания в человеческом мозге кодируются и хранятся в виде матрицы сил межнейронных синаптических связей. На языке электротехники сила межнейронной синаптической связи — это электропроводность синапса, который представляет собой точку электрохимического контакта между дендритом нейрона и нервным волокном. Математический нейрон Мак-Каллока — Питтса — это математическая модель биологического нейрона мозга, учитывающая его структуру и функциональные свойства.
Контрольные вопросы и задания
1.Назовите несколько отличительных признаков в принципах действия современного компьютера, выполненного по схеме Фон Неймана, от мозга.
2.Сколько нейронов имеет человеческий мозг?
3.Сколько дендритов и сколько аксонов может иметь нейрон? Каково их назначение?
4.В каком виде хранится информация в человеческом мозге?
5.Объясните на языке электротехники значение термина «сила синаптической связи». В каких единицах она измеряется?
6.Какой объем памяти имеет человеческий мозг? Сколько чисел он может запомнить?
7.Напишите формулы, с помощью которых происходит преобразование сигналов в математическом нейроне Мак-Каллока—Питтса.
8.Нарисуйте графическое изображение активационной функции математического нейрона Мак-Каллока—Питтса.
9.Нарисуйте математические нейроны, реализующие логические функции «И», «ИЛИ», «НЕТ» и приведите соответствующие им значения сил синаптических связей и порогов.
10.Зайдите на сайт www.LbAi.ru и выполните лабораторную работу № 1 — обучите математический нейрон моделировать функции «И» и «ИЛИ». В случае затруднений или заинтересованности обратитесь к учебно-методическим пособиям [73, 88].
4.3.ПЕРСЕПТРОН РОЗЕНБЛАТТА И ЕГО ОБУЧЕНИЕ
Как отмечалось ранее, американские ученые У. Мак-Каллок и В. Питтс предложили математическую модель нейрона мозга человека, назвав ее математическим нейроном. Так же, как и биологический нейрон, математический нейрон имеет несколько входов и один выход, может существовать в возбужденном и невозбужденном состояниях, причем переход в возбужденное состояние зависит от величины поступающих к нему сигналов и сил межнейронных синаптических связей. Таким образом, математический нейрон весьма правдоподобно имити-

4.3. Персептрон Розенблатта и его обучение 49
Рис. 4.6. Математические нейроны, связанные между собой проводами в нейронную сеть
рует структуру и свойства своего прототипа — биологического нейрона мозга. На этом основании У. Мак-Каллок и В. Питтс в своей статье [100] высказали весьма смелую и даже несколько фантастическую гипотезу, которая впоследствии легла в основу современной нейроинформатики. Они предположили, что если математические нейроны связать между собой проводами, имитирующими нервные волокна мозга (рис. 4.6), и пустить по проводам электрические сигналы, как это происходит в мозге, то такой искусственный мозг будет способен решать интеллектуальные задачи подобно тому, как это делает естественный человеческий мозг!
И эта идея, которую критики называли абсурдной, через 15 лет была блестяще подтверждена американским ученым Фрэнком Розенблаттом [48, 101, 102]. В 1958 г. он создал компьютерную программу для IBM-794, эмулирующую деятельность математических нейронов. Это была первая нейронная сеть или сокращенно — нейросеть. Она была названа персептроном от английского слова perception — осознание.
Затем, спустя два года, Розенблатт смонтировал электронное устройство, в котором функции математических нейронов выполняли отдельные электросхемы, работающие на электронных лампах. Это был первый нейрокомпьютер, который успешно решал сложнейшую интеллектуальную задачу — распознавал буквы латинского алфавита, изображенные на карточках, подносимых к его считывающему устройству — электронному глазу.
Итак, смелую гипотезу Мак-Каллока — Питтса удалось подтвердить экспериментальным путем. Но раз эксперимент удался, значит, правильными оказались наши представления о биологической структуре и строении мозга, о его внутренних электрофизиологических процессах, о способе запоминания и хранения информации. Бы-

50 Глава 4. Понятие о классической нейронной сети
Рис. 4.7. Персептрон, классифицирующий числа на четные и нечетные
ла подтверждена адекватность математического нейрона, как модели биологического нейрона. Была подтверждена адекватность нейросети и нейрокомпьютера, как модели мозга. «Нельзя сказать, что мы точно воспроизводим работу человеческого мозга, — писал Ф. Розенблатт, — но пока персептрон ближе всего к истине».
Разберем принцип действия персептрона на примере решения конкретных задач. На рисунке 4.7 приведен один из простейших вариантов исполнения персептрона, предназначенного для классификации чисел на четные и нечетные. Представим себе матрицу из 12 фотоэлементов, расположенных в виде четырех горизонтальных рядов по три фотоэлемента в каждом ряду. На матрицу фотоэлементов накладывается карточка с изображением цифры, например, «4», (см. рис. 4.7). Если на какой-либо фотоэлемент попадает фрагмент цифры, то этот фотоэлемент вырабатывает сигнал в виде единицы, в противном случае — нуль. На рис. 4.7 на первый фотоэлемент не попал фрагмент цифры, и поэтому его сигнал x1 = 0; на второй фотоэлемент попал фрагмент цифры, и поэтому он вырабатывает сигнал x2 = 1 и т. д.
Согласно формулам (4.1)–(4.2), математический нейрон выполняет суммирование входных сигналов xj, помноженных на синаптические веса wj. Затем результат суммирования S сравнивается с порогом чувствительности θ и вырабатывается выходной сигнал y.
Первоначальные значения синаптических весов wj и порога чувствительности θ Розенблатт задавал датчиком случайных чисел, поэтому
на выходе персептрона случайным образом вырабатывался сигнал: либо 0, либо 1.
Задача состояла в следующем. Требовалось подобрать значения синаптических весов wj такими, чтобы выходной сигнал y принимал
Соседние файлы в папке Реферат
- #
- #
- #
- #
В предыдущей главе мы ознакомились с такими понятиями, как искусственный интеллект, машинное обучение и искусственные нейронные сети.
В этой главе я детально опишу модель искусственного нейрона, расскажу о подходах к обучению сети, а также опишу некоторые известные виды искусственных нейронных сетей, которые мы будем изучать в следующих главах.
Упрощение
В прошлой главе я постоянно говорил о каких-то серьезных упрощениях. Причина упрощений заключается в том, что никакие современные компьютеры не могут быстро моделировать такие сложные системы, как наш мозг. К тому же, как я уже говорил, наш мозг переполнен различными биологическими механизмами, не относящиеся к обработке информации.
Нам нужна модель преобразования входного сигнала в нужный нам выходной. Все остальное нас не волнует. Начинаем упрощать.
Биологическая структура → схема
В предыдущей главе вы поняли, насколько сложно устроены биологические нейронные сети и биологические нейроны. Вместо изображения нейронов в виде чудовищ с щупальцами давайте просто будем рисовать схемы.
Вообще говоря, есть несколько способов графического изображения нейронных сетей и нейронов. Здесь мы будем изображать искусственные нейроны в виде кружков.
Вместо сложного переплетения входов и выходов будем использовать стрелки, обозначающие направление движения сигнала.
Таким образом искусственная нейронная сеть может быть представлена в виде совокупности кружков (искусственных нейронов), связанных стрелками.
Электрические сигналы → числа
В реальной биологической нейронной сети от входов сети к выходам передается электрический сигнал. В процессе прохода по нейронной сети он может изменяться.
Электрический сигнал всегда будет электрическим сигналом. Концептуально ничего не изменяется. Но что же тогда меняется? Меняется величина этого электрического сигнала (сильнее/слабее). А любую величину всегда можно выразить числом (больше/меньше).
В нашей модели искусственной нейронной сети нам совершенно не нужно реализовывать поведение электрического сигнала, так как от его реализации все равно ничего зависеть не будет.
На входы сети мы будем подавать какие-то числа, символизирующие величины электрического сигнала, если бы он был. Эти числа будут продвигаться по сети и каким-то образом меняться. На выходе сети мы получим какое-то результирующее число, являющееся откликом сети.
Для удобства все равно будем называть наши числа, циркулирующие в сети, сигналами.
Синапсы → веса связей
Вспомним картинку из первой главы, на которой цветом были изображены связи между нейронами – синапсы. Синапсы могут усиливать или ослаблять проходящий по ним электрический сигнал.
Давайте характеризовать каждую такую связь определенным числом, называемым весом данной связи. Сигнал, прошедший через данную связь, умножается на вес соответствующей связи.
Это ключевой момент в концепции искусственных нейронных сетей, я объясню его подробнее. Посмотрите на картинку ниже. Теперь каждой черной стрелке (связи) на этой картинке соответствует некоторое число ( w_i ) (вес связи). И когда сигнал проходит по этой связи, его величина умножается на вес этой связи.
На приведенном выше рисунке вес стоит не у каждой связи лишь потому, что там нет места для обозначений. В реальности у каждой ( i )-ой связи свой собственный ( w_i )-ый вес.
Искусственный нейрон
Теперь мы переходим к рассмотрению внутренней структуры искусственного нейрона и того, как он преобразует поступающий на его входы сигнал.
На рисунке ниже представлена полная модель искусственного нейрона.
Не пугайтесь, ничего сложного здесь нет. Давайте рассмотрим все подробно слева направо.
Входы, веса и сумматор
У каждого нейрона, в том числе и у искусственного, должны быть какие-то входы, через которые он принимает сигнал. Мы уже вводили понятие весов, на которые умножаются сигналы, проходящие по связи. На картинке выше веса изображены кружками.
Поступившие на входы сигналы умножаются на свои веса. Сигнал первого входа ( x_1 ) умножается на соответствующий этому входу вес ( w_1 ). В итоге получаем ( x_1w_1 ). И так до ( n )-ого входа. В итоге на последнем входе получаем ( x_nw_n ).
Теперь все произведения передаются в сумматор. Уже исходя из его названия можно понять, что он делает. Он просто суммирует все входные сигналы, умноженные на соответствующие веса:
[ x_1w_1+x_2w_2+cdots+x_nw_n = sumlimits^n_{i=1}x_iw_i ]
Результатом работы сумматора является число, называемое взвешенной суммой.
Взвешенная сумма (Weighted sum) (( net )) — сумма входных сигналов, умноженных на соответствующие им веса.
[ net=sumlimits^n_{i=1}x_iw_i ]
Роль сумматора очевидна – он агрегирует все входные сигналы (которых может быть много) в какое-то одно число – взвешенную сумму, которая характеризует поступивший на нейрон сигнал в целом. Еще взвешенную сумму можно представить как степень общего возбуждения нейрона.
Пример
Для понимания роли последнего компонента искусственного нейрона – функции активации – я приведу аналогию.
Давайте рассмотрим один искусственный нейрон. Его задача – решить, ехать ли отдыхать на море. Для этого на его входы мы подаем различные данные. Пусть у нашего нейрона будет 4 входа:
- Стоимость поездки
- Какая на море погода
- Текущая обстановка с работой
- Будет ли на пляже закусочная
Все эти параметры будем характеризовать 0 или 1. Соответственно, если погода на море хорошая, то на этот вход подаем 1. И так со всеми остальными параметрами.
Если у нейрона есть четыре входа, то должно быть и четыре весовых коэффициента. В нашем примере весовые коэффициенты можно представить как показатели важности каждого входа, влияющие на общее решение нейрона. Веса входов распределим следующим образом:
- 5
- 4
- 1
- 1
Нетрудно заметить, что очень большую роль играют факторы стоимости и погоды на море (первые два входа). Они же и будут играть решающую роль при принятии нейроном решения.
Пусть на входы нашего нейрона мы подаем следующие сигналы:
- 1
- 0
- 0
- 1
Умножаем веса входов на сигналы соответствующих входов:
- 5
- 0
- 0
- 1
Взвешенная сумма для такого набора входных сигналов равна 6:
[ net=sumlimits^4_{i=1}x_iw_i = 5 + 0 + 0 + 1 =6 ]
Все классно, но что делать дальше? Как нейрон должен решить, ехать на море или нет? Очевидно, нам нужно как-то преобразовать нашу взвешенную сумму и получить ответ.
Вот на сцену выходит функция активации.
Функция активации
Просто так подавать взвешенную сумму на выход достаточно бессмысленно. Нейрон должен как-то обработать ее и сформировать адекватный выходной сигнал. Именно для этих целей и используют функцию активации.
Она преобразует взвешенную сумму в какое-то число, которое и является выходом нейрона (выход нейрона обозначим переменной ( out )).
Для разных типов искусственных нейронов используют самые разные функции активации. В общем случае их обозначают символом ( phi(net) ). Указание взвешенного сигнала в скобках означает, что функция активации принимает взвешенную сумму как параметр.
Функция активации (Activation function) (( phi(net) )) — функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона (( out )).
[ out=phi(net) ]
Далее мы подробно рассмотрим самые известные функции активации.
Функция единичного скачка
Самый простой вид функции активации. Выход нейрона может быть равен только 0 или 1. Если взвешенная сумма больше определенного порога ( b ), то выход нейрона равен 1. Если ниже, то 0.
Как ее можно использовать? Предположим, что мы поедем на море только тогда, когда взвешенная сумма больше или равна 5. Значит наш порог равен 5:
[ b=5 ]
В нашем примере взвешенная сумма равнялась 6, а значит выходной сигнал нашего нейрона равен 1. Итак, мы едем на море.
Однако если бы погода на море была бы плохой, а также поездка была бы очень дорогой, но имелась бы закусочная и обстановка с работой нормальная (входы: 0011), то взвешенная сумма равнялась бы 2, а значит выход нейрона равнялся бы 0. Итак, мы никуда не едем.
В общем, нейрон смотрит на взвешенную сумму и если она получается больше его порога, то нейрон выдает выходной сигнал, равный 1.
Графически эту функцию активации можно изобразить следующим образом.
На горизонтальной оси расположены величины взвешенной суммы. На вертикальной оси — значения выходного сигнала. Как легко видеть, возможны только два значения выходного сигнала: 0 или 1. Причем 0 будет выдаваться всегда от минус бесконечности и вплоть до некоторого значения взвешенной суммы, называемого порогом. Если взвешенная сумма равна порогу или больше него, то функция выдает 1. Все предельно просто.
Теперь запишем эту функцию активации математически. Почти наверняка вы сталкивались с таким понятием, как составная функция. Это когда мы под одной функцией объединяем несколько правил, по которым рассчитывается ее значение. В виде составной функции функция единичного скачка будет выглядеть следующим образом:
[ out(net) = begin{cases} 0, net < b \ 1, net geq b end{cases} ]
В этой записи нет ничего сложного. Выход нейрона (( out )) зависит от взвешенной суммы (( net )) следующим образом: если ( net ) (взвешенная сумма) меньше какого-то порога (( b )), то ( out ) (выход нейрона) равен 0. А если ( net ) больше или равен порогу ( b ), то ( out ) равен 1.
Сигмоидальная функция
На самом деле существует целое семейство сигмоидальных функций, некоторые из которых применяют в качестве функции активации в искусственных нейронах.
Все эти функции обладают некоторыми очень полезными свойствами, ради которых их и применяют в нейронных сетях. Эти свойства станут очевидными после того, как вы увидите графики этих функций.
Итак… самая часто используемая в нейронных сетях сигмоида — логистическая функция.
График этой функции выглядит достаточно просто. Если присмотреться, то можно увидеть некоторое подобие английской буквы ( S ), откуда и пошло название семейства этих функций.
А вот так она записывается аналитически:
[ out(net)=frac{1}{1+exp(-a cdot net)} ]
Что за параметр ( a )? Это какое-то число, которое характеризует степень крутизны функции. Ниже представлены логистические функции с разным параметром ( a ).
Вспомним наш искусственный нейрон, определяющий, надо ли ехать на море. В случае с функцией единичного скачка все было очевидно. Мы либо едем на море (1), либо нет (0).
Здесь же случай более приближенный к реальности. Мы до конца полностью не уверены (в особенности, если вы параноик) – стоит ли ехать? Тогда использование логистической функции в качестве функции активации приведет к тому, что вы будете получать цифру между 0 и 1. Причем чем больше взвешенная сумма, тем ближе выход будет к 1 (но никогда не будет точно ей равен). И наоборот, чем меньше взвешенная сумма, тем ближе выход нейрона будет к 0.
Например, выход нашего нейрона равен 0.8. Это значит, что он считает, что поехать на море все-таки стоит. Если бы его выход был бы равен 0.2, то это означает, что он почти наверняка против поездки на море.
Какие же замечательные свойства имеет логистическая функция?
- она является «сжимающей» функцией, то есть вне зависимости от аргумента (взвешенной суммы), выходной сигнал всегда будет в пределах от 0 до 1
- она более гибкая, чем функция единичного скачка – ее результатом может быть не только 0 и 1, но и любое число между ними
- во всех точках она имеет производную, и эта производная может быть выражена через эту же функцию
Именно из-за этих свойств логистическая функция чаще всего используются в качестве функции активации в искусственных нейронах.
Гиперболический тангенс
Однако есть и еще одна сигмоида – гиперболический тангенс. Он применяется в качестве функции активации биологами для более реалистичной модели нервной клетки.
Такая функция позволяет получить на выходе значения разных знаков (например, от -1 до 1), что может быть полезным для ряда сетей.
Функция записывается следующим образом:
[ out(net) = tanhleft(frac{net}{a}right) ]
В данной выше формуле параметр ( a ) также определяет степень крутизны графика этой функции.
А вот так выглядит график этой функции.
Как видите, он похож на график логистической функции. Гиперболический тангенс обладает всеми полезными свойствами, которые имеет и логистическая функция.
Что мы узнали?
Теперь вы получили полное представление о внутренней структуре искусственного нейрона. Я еще раз приведу краткое описание его работы.
У нейрона есть входы. На них подаются сигналы в виде чисел. Каждый вход имеет свой вес (тоже число). Сигналы на входе умножаются на соответствующие веса. Получаем набор «взвешенных» входных сигналов.
Далее этот набор попадает в сумматор, которой просто складывает все входные сигналы, помноженные на веса. Получившееся число называют взвешенной суммой.
Затем взвешенная сумма преобразуется функцией активации и мы получаем выход нейрона.
Сформулируем теперь самое короткое описание работы нейрона – его математическую модель:
Математическая модель искусственного нейрона с ( n ) входами:
[ out=phileft(sumlimits^n_{i=1}x_iw_iright) ]
где
( phi ) – функция активации
( sumlimits^n_{i=1}x_iw_i ) – взвешенная сумма, как сумма ( n ) произведений входных сигналов на соответствующие веса.
Виды ИНС
Мы разобрались со структурой искусственного нейрона. Искусственные нейронные сети состоят из совокупности искусственных нейронов. Возникает логичный вопрос – а как располагать/соединять друг с другом эти самые искусственные нейроны?
Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу – распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений.
А дальше начинаются различия…
Однослойные нейронные сети
В однослойных нейронных сетях сигналы с входного слоя сразу подаются на выходной слой. Он производит необходимые вычисления, результаты которых сразу подаются на выходы.
Выглядит однослойная нейронная сеть следующим образом:
На этой картинке входной слой обозначен кружками (он не считается за слой нейронной сети), а справа расположен слой обычных нейронов.
Нейроны соединены друг с другом стрелками. Над стрелками расположены веса соответствующих связей (весовые коэффициенты).
Однослойная нейронная сеть (Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.
Многослойные нейронные сети
Такие сети, помимо входного и выходного слоев нейронов, характеризуются еще и скрытым слоем (слоями). Понять их расположение просто – эти слои находятся между входным и выходным слоями.
Такая структура нейронных сетей копирует многослойную структуру определенных отделов мозга.
Название скрытый слой получил неслучайно. Дело в том, что только относительно недавно были разработаны методы обучения нейронов скрытого слоя. До этого обходились только однослойными нейросетями.
Многослойные нейронные сети обладают гораздо большими возможностями, чем однослойные.
Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.
Многослойная нейронная сеть (Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.
Сети прямого распространения
Можно заметить одну очень интересную деталь на картинках нейросетей в примерах выше.
Во всех примерах стрелки строго идут слева направо, то есть сигнал в таких сетях идет строго от входного слоя к выходному.
Сети прямого распространения (Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.
Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.
Однако никто не запрещает сигналу идти и в обратную сторону.
Сети с обратными связями
В сетях такого типа сигнал может идти и в обратную сторону. В чем преимущество?
Дело в том, что в сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах.
А в сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).
Возможность сигналов циркулировать в сети открывает новые, удивительные возможности нейронных сетей. С помощью таких сетей можно создавать нейросети, восстанавливающие или дополняющие сигналы. Другими словами такие нейросети имеют свойства кратковременной памяти (как у человека).
Сети с обратными связями (Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.
Обучение нейронной сети
Теперь давайте чуть более подробно рассмотрим вопрос обучения нейронной сети. Что это такое? И каким образом это происходит?
Что такое обучение сети?
Искусственная нейронная сеть – это совокупность искусственных нейронов. Теперь давайте возьмем, например, 100 нейронов и соединим их друг с другом. Ясно, что при подаче сигнала на вход, мы получим что-то бессмысленное на выходе.
Значит нам надо менять какие-то параметры сети до тех пор, пока входной сигнал не преобразуется в нужный нам выходной.
Что мы можем менять в нейронной сети?
Изменять общее количество искусственных нейронов бессмысленно по двум причинам. Во-первых, увеличение количества вычислительных элементов в целом лишь делает систему тяжеловеснее и избыточнее. Во-вторых, если вы соберете 1000 дураков вместо 100, то они все-равно не смогут правильно ответить на вопрос.
Сумматор изменить не получится, так как он выполняет одну жестко заданную функцию – складывать. Если мы его заменим на что-то или вообще уберем, то это вообще уже не будет искусственным нейроном.
Если менять у каждого нейрона функцию активации, то мы получим слишком разношерстную и неконтролируемую нейронную сеть. К тому же, в большинстве случаев нейроны в нейронных сетях одного типа. То есть они все имеют одну и ту же функцию активации.
Остается только один вариант – менять веса связей.
Обучение нейронной сети (Training) — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Такой подход к термину «обучение нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей. Каждая из них в отдельности состоит из нейронов одного типа (функция активации одинаковая). Мы обучаемся благодаря изменению синапсов – элементов, которые усиливают/ослабляют входной сигнал.
Однако есть еще один важный момент. Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ». Со стороны будет казаться, что она очень быстро «обучилась». И как только вы подадите немного измененный сигнал, ожидая увидеть правильный ответ, то сеть выдаст бессмыслицу.
В самом деле, зачем нам сеть, определяющая лицо только на одном фото. Мы ждем от сети способности обобщать какие-то признаки и узнавать лица и на других фотографиях тоже.
Именно с этой целью и создаются обучающие выборки.
Обучающая выборка (Training set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике.
Однако прежде чем пускать свежеиспеченную нейросеть в бой, часто производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка (Testing set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Мы поняли, что такое «обучение сети» – подбор правильного набора весов. Теперь возникает вопрос – а как можно обучать сеть? В самом общем случае есть два подхода, приводящие к разным результатам: обучение с учителем и обучение без учителя.
Обучение с учителем
Суть данного подхода заключается в том, что вы даете на вход сигнал, смотрите на ответ сети, а затем сравниваете его с уже готовым, правильным ответом.
Важный момент. Не путайте правильные ответы и известный алгоритм решения! Вы можете обвести пальцем лицо на фото (правильный ответ), но не сможете сказать, как это сделали (известный алгоритм). Тут такая же ситуация.
Затем, с помощью специальных алгоритмов, вы меняете веса связей нейронной сети и снова даете ей входной сигнал. Сравниваете ее ответ с правильным и повторяете этот процесс до тех пор, пока сеть не начнет отвечать с приемлемой точностью (как я говорил в 1 главе, однозначно точных ответов сеть давать не может).
Обучение с учителем (Supervised learning) — вид обучения сети, при котором ее веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
Где взять правильные ответы?
Если мы хотим, чтобы сеть узнавала лица, мы можем создать обучающую выборку на 1000 фотографий (входные сигналы) и самостоятельно выделить на ней лица (правильные ответы).
Если мы хотим, чтобы сеть прогнозировала рост/падение цен, то обучающую выборку надо делать, основываясь на прошлых данных. В качестве входных сигналов можно брать определенные дни, общее состояние рынка и другие параметры. А в качестве правильных ответов – рост и падение цены в те дни.
И так далее…
Стоит отметить, что учитель, конечно же, не обязательно человек. Дело в том, что порой сеть приходится тренировать часами и днями, совершая тысячи и десятки тысяч попыток. В 99% случаев эту роль выполняет компьютер, а точнее, специальная компьютерная программа.
Обучение без учителя
Обучение без учителя применяют тогда, когда у нас нет правильных ответов на входные сигналы. В этом случае вся обучающая выборка состоит из набора входных сигналов.
Что же происходит при таком обучении сети? Оказывается, что при таком «обучении» сеть начинает выделять классы подаваемых на вход сигналов. Короче говоря – сеть начинает кластеризацию.
Например, вы демонстрируете сети конфеты, пирожные и торты. Вы никак не регулируете работу сети. Вы просто подаете на ее входы данные о данном объекте. Со временем сеть начнет выдавать сигналы трех разных типов, которые и отвечают за объекты на входе.
Обучение без учителя (Unsupervised learning) — вид обучения сети, при котором сеть самостоятельно классифицирует входные сигналы. Правильные (эталонные) выходные сигналы не демонстрируются.
Выводы
В этой главе вы узнали все о структуре искусственного нейрона, а также получили полное представление о том, как он работает (и о его математической модели).
Более того, вы теперь знаете о различных видах искусственных нейронных сетей: однослойные, многослойные, а также feedforward сети и сети с обратными связями.
Вы также ознакомились с тем, что представляет собой обучение сети с учителем и без учителя.
Вы уже знаете необходимую теорию. Последующие главы – рассмотрение конкретных видов нейронных сетей, конкретные алгоритмы их обучения и практика программирования.
Вопросы и задачи
Материал этой главы надо знать очень хорошо, так как в ней содержатся основные теоретические сведения по искусственным нейронным сетям. Обязательно добейтесь уверенных и правильных ответов на все нижеприведенные вопросы и задачи.
Опишите упрощения ИНС по сравнению с биологическими нейросетями.
Из каких элементов состоит искусственный нейрон?
Что такое взвешенная сумма? Какой компонент искусственного нейрона ее вычисляет?
Вычислите взвешенную сумму нейрона (рисунок выше)
Что такое функция активации?
Запишите математическую модель искусственного нейрона.
Чем отличаются однослойные и многослойные нейронные сети?
В чем отличие feedforward сетей от сетей с обратными связями?
Что такое обучающая выборка? В чем ее смысл?
Что понимают под обучением сети?
Что такое обучение с учителем и без него?
From Wikipedia, the free encyclopedia
An artificial neuron is a mathematical function conceived as a model of biological neurons, a neural network. Artificial neurons are elementary units in an artificial neural network.[1] The artificial neuron receives one or more inputs (representing excitatory postsynaptic potentials and inhibitory postsynaptic potentials at neural dendrites) and sums them to produce an output (or activation, representing a neuron’s action potential which is transmitted along its axon). Usually each input is separately weighted, and the sum is passed through a non-linear function known as an activation function or transfer function[clarification needed]. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. Non-monotonic, unbounded and oscillating activation functions with multiple zeros that outperform sigmoidal and ReLU like activation functions on many tasks have also been recently explored. The thresholding function has inspired building logic gates referred to as threshold logic; applicable to building logic circuits resembling brain processing. For example, new devices such as memristors have been extensively used to develop such logic in recent times.[2]
The artificial neuron transfer function should not be confused with a linear system’s transfer function.
Artificial neurons can also refer to artificial cells in neuromorphic engineering (see below) that are similar to natural physical neurons.
Basic structure[edit]
For a given artificial neuron k, let there be m + 1 inputs with signals x0 through xm and weights wk0 through wkm. Usually, the x0 input is assigned the value +1, which makes it a bias input with wk0 = bk. This leaves only m actual inputs to the neuron: from x1 to xm.
The output of the kth neuron is:
Where 
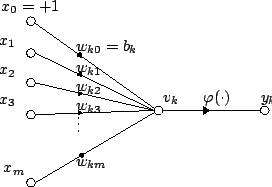
The output is analogous to the axon of a biological neuron, and its value propagates to the input of the next layer, through a synapse. It may also exit the system, possibly as part of an output vector.
It has no learning process as such. Its transfer function weights are calculated and threshold value are predetermined.
Types[edit]
Depending on the specific model used they may be called a semi-linear unit, Nv neuron, binary neuron, linear threshold function, or McCulloch–Pitts (MCP) neuron.
Simple artificial neurons, such as the McCulloch–Pitts model, are sometimes described as «caricature models», since they are intended to reflect one or more neurophysiological observations, but without regard to realism.[3]
|
This section needs expansion. You can help by adding to it. (May 2017) |
Biological models[edit]
Neuron and myelinated axon, with signal flow from inputs at dendrites to outputs at axon terminals
Artificial neurons are designed to mimic aspects of their biological counterparts. However a significant performance gap exists between biological and artificial neural networks. In particular single biological neurons in the human brain with oscillating activation function capable of learning the XOR function have been discovered.[4]
- Dendrites – In a biological neuron, the dendrites act as the input vector. These dendrites allow the cell to receive signals from a large (>1000) number of neighboring neurons. As in the above mathematical treatment, each dendrite is able to perform «multiplication» by that dendrite’s «weight value.» The multiplication is accomplished by increasing or decreasing the ratio of synaptic neurotransmitters to signal chemicals introduced into the dendrite in response to the synaptic neurotransmitter. A negative multiplication effect can be achieved by transmitting signal inhibitors (i.e. oppositely charged ions) along the dendrite in response to the reception of synaptic neurotransmitters.
- Soma – In a biological neuron, the soma acts as the summation function, seen in the above mathematical description. As positive and negative signals (exciting and inhibiting, respectively) arrive in the soma from the dendrites, the positive and negative ions are effectively added in summation, by simple virtue of being mixed together in the solution inside the cell’s body.
- Axon – The axon gets its signal from the summation behavior which occurs inside the soma. The opening to the axon essentially samples the electrical potential of the solution inside the soma. Once the soma reaches a certain potential, the axon will transmit an all-in signal pulse down its length. In this regard, the axon behaves as the ability for us to connect our artificial neuron to other artificial neurons.
Unlike most artificial neurons, however, biological neurons fire in discrete pulses. Each time the electrical potential inside the soma reaches a certain threshold, a pulse is transmitted down the axon. This pulsing can be translated into continuous values. The rate (activations per second, etc.) at which an axon fires converts directly into the rate at which neighboring cells get signal ions introduced into them. The faster a biological neuron fires, the faster nearby neurons accumulate electrical potential (or lose electrical potential, depending on the «weighting» of the dendrite that connects to the neuron that fired). It is this conversion that allows computer scientists and mathematicians to simulate biological neural networks using artificial neurons which can output distinct values (often from −1 to 1).
Encoding[edit]
Research has shown that unary coding is used in the neural circuits responsible for birdsong production.[5][6] The use of unary in biological networks is presumably due to the inherent simplicity of the coding. Another contributing factor could be that unary coding provides a certain degree of error correction.[7]
Physical artificial cells[edit]
There is research and development into physical artificial neurons – organic and inorganic.
For example, some artificial neurons can receive[8][9] and release dopamine (chemical signals rather than electrical signals) and communicate with natural rat muscle and brain cells, with potential for use in BCIs/prosthetics.[10][11]
Low-power biocompatible memristors may enable construction of artificial neurons which function at voltages of biological action potentials and could be used to directly process biosensing signals, for neuromorphic computing and/or direct communication with biological neurons.[12][13][14]
Organic neuromorphic circuits made out of polymers, coated with an ion-rich gel to enable a material to carry an electric charge like real neurons, have been built into a robot, enabling it to learn sensorimotorically within the real world, rather than via simulations or virtually.[15][16] Moreover, artificial spiking neurons made of soft matter (polymers) can operate in biologically relevant environments and enable the synergetic communication between the artificial and biological domains.[17][18]
History[edit]
The first artificial neuron was the Threshold Logic Unit (TLU), or Linear Threshold Unit,[19] first proposed by Warren McCulloch and Walter Pitts in 1943. The model was specifically targeted as a computational model of the «nerve net» in the brain.[20] As a transfer function, it employed a threshold, equivalent to using the Heaviside step function. Initially, only a simple model was considered, with binary inputs and outputs, some restrictions on the possible weights, and a more flexible threshold value. Since the beginning it was already noticed that any boolean function could be implemented by networks of such devices, what is easily seen from the fact that one can implement the AND and OR functions, and use them in the disjunctive or the conjunctive normal form.
Researchers also soon realized that cyclic networks, with feedbacks through neurons, could define dynamical systems with memory, but most of the research concentrated (and still does) on strictly feed-forward networks because of the smaller difficulty they present.
One important and pioneering artificial neural network that used the linear threshold function was the perceptron, developed by Frank Rosenblatt. This model already considered more flexible weight values in the neurons, and was used in machines with adaptive capabilities. The representation of the threshold values as a bias term was introduced by Bernard Widrow in 1960 – see ADALINE.
In the late 1980s, when research on neural networks regained strength, neurons with more continuous shapes started to be considered. The possibility of differentiating the activation function allows the direct use of the gradient descent and other optimization algorithms for the adjustment of the weights. Neural networks also started to be used as a general function approximation model. The best known training algorithm called backpropagation has been rediscovered several times but its first development goes back to the work of Paul Werbos.[21][22]
Types of transfer functions[edit]
The transfer function (activation function) of a neuron is chosen to have a number of properties which either enhance or simplify the network containing the neuron. Crucially, for instance, any multilayer perceptron using a linear transfer function has an equivalent single-layer network; a non-linear function is therefore necessary to gain the advantages of a multi-layer network.[citation needed]
Below, u refers in all cases to the weighted sum of all the inputs to the neuron, i.e. for n inputs,
where w is a vector of synaptic weights and x is a vector of inputs.
Step function[edit]
The output y of this transfer function is binary, depending on whether the input meets a specified threshold, θ. The «signal» is sent, i.e. the output is set to one, if the activation meets the threshold.
This function is used in perceptrons and often shows up in many other models. It performs a division of the space of inputs by a hyperplane. It is specially useful in the last layer of a network intended to perform binary classification of the inputs. It can be approximated from other sigmoidal functions by assigning large values to the weights.
Linear combination[edit]
In this case, the output unit is simply the weighted sum of its inputs plus a bias term. A number of such linear neurons perform a linear transformation of the input vector. This is usually more useful in the first layers of a network. A number of analysis tools exist based on linear models, such as harmonic analysis, and they can all be used in neural networks with this linear neuron. The bias term allows us to make affine transformations to the data.
See: Linear transformation, Harmonic analysis, Linear filter, Wavelet, Principal component analysis, Independent component analysis, Deconvolution.
Sigmoid[edit]
A fairly simple non-linear function, the sigmoid function such as the logistic function also has an easily calculated derivative, which can be important when calculating the weight updates in the network. It thus makes the network more easily manipulable mathematically, and was attractive to early computer scientists who needed to minimize the computational load of their simulations. It was previously commonly seen in multilayer perceptrons. However, recent work has shown sigmoid neurons to be less effective than rectified linear neurons. The reason is that the gradients computed by the backpropagation algorithm tend to diminish towards zero as activations propagate through layers of sigmoidal neurons, making it difficult to optimize neural networks using multiple layers of sigmoidal neurons.
Rectifier[edit]
In the context of artificial neural networks, the rectifier or ReLU (Rectified Linear Unit) is an activation function defined as the positive part of its argument:
where x is the input to a neuron. This is also known as a ramp function and is analogous to half-wave rectification in electrical engineering. This activation function was first introduced to a dynamical network by Hahnloser et al. in a 2000 paper in Nature[23] with strong biological motivations and mathematical justifications.[24] It has been demonstrated for the first time in 2011 to enable better training of deeper networks,[25] compared to the widely used activation functions prior to 2011, i.e., the logistic sigmoid (which is inspired by probability theory; see logistic regression) and its more practical[26] counterpart, the hyperbolic tangent.
A commonly used variant of the ReLU activation function is the Leaky ReLU which allows a small, positive gradient when the unit is not active:

where x is the input to the neuron and a is a small positive constant (in the original paper the value 0.01 was used for a).[27]
Pseudocode algorithm[edit]
The following is a simple pseudocode implementation of a single TLU which takes boolean inputs (true or false), and returns a single boolean output when activated. An object-oriented model is used. No method of training is defined, since several exist. If a purely functional model were used, the class TLU below would be replaced with a function TLU with input parameters threshold, weights, and inputs that returned a boolean value.
class TLU defined as:
data member threshold : number
data member weights : list of numbers of size X
function member fire(inputs : list of booleans of size X) : boolean defined as:
variable T : number
T ← 0
for each i in 1 to X do
if inputs(i) is true then
T ← T + weights(i)
end if
end for each
if T > threshold then
return true
else:
return false
end if
end function
end class
See also[edit]
- Binding neuron
- Connectionism
References[edit]
- ^ «Neuromorphic Circuits With Neural Modulation Enhancing the Information Content of Neural Signaling | International Conference on Neuromorphic Systems 2020». doi:10.1145/3407197.3407204. S2CID 220794387.
- ^ Maan, A. K.; Jayadevi, D. A.; James, A. P. (1 January 2016). «A Survey of Memristive Threshold Logic Circuits». IEEE Transactions on Neural Networks and Learning Systems. PP (99): 1734–1746. arXiv:1604.07121. Bibcode:2016arXiv160407121M. doi:10.1109/TNNLS.2016.2547842. ISSN 2162-237X. PMID 27164608. S2CID 1798273.
- ^
F. C. Hoppensteadt and E. M. Izhikevich (1997). Weakly connected neural networks. Springer. p. 4. ISBN 978-0-387-94948-2. - ^ Gidon, Albert; Zolnik, Timothy Adam; Fidzinski, Pawel; Bolduan, Felix; Papoutsi, Athanasia; Poirazi, Panayiota; Holtkamp, Martin; Vida, Imre; Larkum, Matthew Evan (2020-01-03). «Dendritic action potentials and computation in human layer 2/3 cortical neurons». Science. 367 (6473): 83–87. Bibcode:2020Sci…367…83G. doi:10.1126/science.aax6239. PMID 31896716. S2CID 209676937.
- ^ Squire, L.; Albright, T.; Bloom, F.; Gage, F.; Spitzer, N., eds. (October 2007). Neural network models of birdsong production, learning, and coding (PDF). New Encyclopedia of Neuroscience: Elservier. Archived from the original (PDF) on 2015-04-12. Retrieved 12 April 2015.
- ^ Moore, J.M.; et al. (2011). «Motor pathway convergence predicts syllable repertoire size in oscine birds». Proc. Natl. Acad. Sci. USA. 108 (39): 16440–16445. Bibcode:2011PNAS..10816440M. doi:10.1073/pnas.1102077108. PMC 3182746. PMID 21918109.
- ^ Potluri, Pushpa Sree (26 November 2014). «Error Correction Capacity of Unary Coding». arXiv:1411.7406 [cs.IT].
- ^ Kleiner, Kurt (25 August 2022). «Making computer chips act more like brain cells». Knowable Magazine | Annual Reviews. doi:10.1146/knowable-082422-1. Retrieved 23 September 2022.
- ^ Keene, Scott T.; Lubrano, Claudia; Kazemzadeh, Setareh; Melianas, Armantas; Tuchman, Yaakov; Polino, Giuseppina; Scognamiglio, Paola; Cinà, Lucio; Salleo, Alberto; van de Burgt, Yoeri; Santoro, Francesca (September 2020). «A biohybrid synapse with neurotransmitter-mediated plasticity». Nature Materials. 19 (9): 969–973. Bibcode:2020NatMa..19..969K. doi:10.1038/s41563-020-0703-y. ISSN 1476-4660. PMID 32541935. S2CID 219691307.
- University press release: «Researchers develop artificial synapse that works with living cells». Stanford University via medicalxpress.com. Retrieved 23 September 2022.
- ^ «Artificial neuron swaps dopamine with rat brain cells like a real one». New Scientist. Retrieved 16 September 2022.
- ^ Wang, Ting; Wang, Ming; Wang, Jianwu; Yang, Le; Ren, Xueyang; Song, Gang; Chen, Shisheng; Yuan, Yuehui; Liu, Ruiqing; Pan, Liang; Li, Zheng; Leow, Wan Ru; Luo, Yifei; Ji, Shaobo; Cui, Zequn; He, Ke; Zhang, Feilong; Lv, Fengting; Tian, Yuanyuan; Cai, Kaiyu; Yang, Bowen; Niu, Jingyi; Zou, Haochen; Liu, Songrui; Xu, Guoliang; Fan, Xing; Hu, Benhui; Loh, Xian Jun; Wang, Lianhui; Chen, Xiaodong (8 August 2022). «A chemically mediated artificial neuron». Nature Electronics. 5 (9): 586–595. doi:10.1038/s41928-022-00803-0. ISSN 2520-1131. S2CID 251464760.
- ^ «Scientists create tiny devices that work like the human brain». The Independent. April 20, 2020. Archived from the original on April 24, 2020. Retrieved May 17, 2020.
- ^ «Researchers unveil electronics that mimic the human brain in efficient learning». phys.org. Archived from the original on May 28, 2020. Retrieved May 17, 2020.
- ^ Fu, Tianda; Liu, Xiaomeng; Gao, Hongyan; Ward, Joy E.; Liu, Xiaorong; Yin, Bing; Wang, Zhongrui; Zhuo, Ye; Walker, David J. F.; Joshua Yang, J.; Chen, Jianhan; Lovley, Derek R.; Yao, Jun (April 20, 2020). «Bioinspired bio-voltage memristors». Nature Communications. 11 (1): 1861. Bibcode:2020NatCo..11.1861F. doi:10.1038/s41467-020-15759-y. PMC 7171104. PMID 32313096.
- ^ Bolakhe, Saugat. «Lego Robot with an Organic ‘Brain’ Learns to Navigate a Maze». Scientific American. Retrieved 1 February 2022.
- ^ Krauhausen, Imke; Koutsouras, Dimitrios A.; Melianas, Armantas; Keene, Scott T.; Lieberth, Katharina; Ledanseur, Hadrien; Sheelamanthula, Rajendar; Giovannitti, Alexander; Torricelli, Fabrizio; Mcculloch, Iain; Blom, Paul W. M.; Salleo, Alberto; Burgt, Yoeri van de; Gkoupidenis, Paschalis (December 2021). «Organic neuromorphic electronics for sensorimotor integration and learning in robotics». Science Advances. 7 (50): eabl5068. Bibcode:2021SciA….7.5068K. doi:10.1126/sciadv.abl5068. hdl:10754/673986. PMC 8664264. PMID 34890232. S2CID 245046482.
- ^ Sarkar, Tanmoy; Lieberth, Katharina; Pavlou, Aristea; Frank, Thomas; Mailaender, Volker; McCulloch, Iain; Blom, Paul W. M.; Torriccelli, Fabrizio; Gkoupidenis, Paschalis (7 November 2022). «An organic artificial spiking neuron for in situ neuromorphic sensing and biointerfacing». Nature Electronics. 5 (11): 774–783. doi:10.1038/s41928-022-00859-y. ISSN 2520-1131. S2CID 253413801.
- ^ «Artificial neurons emulate biological counterparts to enable synergetic operation». Nature Electronics. 5 (11): 721–722. 10 November 2022. doi:10.1038/s41928-022-00862-3. ISSN 2520-1131. S2CID 253469402.
- ^ Martin Anthony (January 2001). Discrete Mathematics of Neural Networks: Selected Topics. SIAM. pp. 3–. ISBN 978-0-89871-480-7.
- ^ Charu C. Aggarwal (25 July 2014). Data Classification: Algorithms and Applications. CRC Press. pp. 209–. ISBN 978-1-4665-8674-1.
- ^ Paul Werbos, Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences. PhD thesis, Harvard University, 1974
- ^ Werbos, P.J. (1990). «Backpropagation through time: what it does and how to do it». Proceedings of the IEEE. 78 (10): 1550–1560. doi:10.1109/5.58337. ISSN 0018-9219. S2CID 18470994.
- ^ Hahnloser, Richard H. R.; Sarpeshkar, Rahul; Mahowald, Misha A.; Douglas, Rodney J.; Seung, H. Sebastian (2000). «Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit». Nature. 405 (6789): 947–951. Bibcode:2000Natur.405..947H. doi:10.1038/35016072. ISSN 0028-0836. PMID 10879535. S2CID 4399014.
- ^ R Hahnloser, H.S. Seung (2001). Permitted and Forbidden Sets in Symmetric Threshold-Linear Networks. NIPS 2001.
{{cite conference}}: CS1 maint: uses authors parameter (link) - ^ Xavier Glorot, Antoine Bordes and Yoshua Bengio (2011). Deep sparse rectifier neural networks (PDF). AISTATS.
{{cite conference}}: CS1 maint: uses authors parameter (link) - ^ Yann LeCun, Leon Bottou, Genevieve B. Orr and Klaus-Robert Müller (1998). «Efficient BackProp» (PDF). In G. Orr; K. Müller (eds.). Neural Networks: Tricks of the Trade. Springer.
{{cite encyclopedia}}: CS1 maint: uses authors parameter (link) - ^ Andrew L. Maas, Awni Y. Hannun, Andrew Y. Ng (2014). Rectifier Nonlinearities Improve Neural Network Acoustic Models.
Further reading[edit]
- McCulloch, Warren S.; Pitts, Walter (1943). «A logical calculus of the ideas immanent in nervous activity». Bulletin of Mathematical Biophysics. 5 (4): 115–133. doi:10.1007/bf02478259.
- Samardak, A.; Nogaret, A.; Janson, N. B.; Balanov, A. G.; Farrer, I.; Ritchie, D. A. (2009-06-05). «Noise-Controlled Signal Transmission in a Multithread Semiconductor Neuron». Physical Review Letters. 102 (22): 226802. Bibcode:2009PhRvL.102v6802S. doi:10.1103/physrevlett.102.226802. PMID 19658886. S2CID 11211062.
External links[edit]
- Artifical [sic] neuron mimicks function of human cells
- McCulloch-Pitts Neurons (Overview)