В предыдущей главе мы ознакомились с такими понятиями, как искусственный интеллект, машинное обучение и искусственные нейронные сети.
В этой главе я детально опишу модель искусственного нейрона, расскажу о подходах к обучению сети, а также опишу некоторые известные виды искусственных нейронных сетей, которые мы будем изучать в следующих главах.
Упрощение
В прошлой главе я постоянно говорил о каких-то серьезных упрощениях. Причина упрощений заключается в том, что никакие современные компьютеры не могут быстро моделировать такие сложные системы, как наш мозг. К тому же, как я уже говорил, наш мозг переполнен различными биологическими механизмами, не относящиеся к обработке информации.
Нам нужна модель преобразования входного сигнала в нужный нам выходной. Все остальное нас не волнует. Начинаем упрощать.
Биологическая структура → схема
В предыдущей главе вы поняли, насколько сложно устроены биологические нейронные сети и биологические нейроны. Вместо изображения нейронов в виде чудовищ с щупальцами давайте просто будем рисовать схемы.
Вообще говоря, есть несколько способов графического изображения нейронных сетей и нейронов. Здесь мы будем изображать искусственные нейроны в виде кружков.
Вместо сложного переплетения входов и выходов будем использовать стрелки, обозначающие направление движения сигнала.
Таким образом искусственная нейронная сеть может быть представлена в виде совокупности кружков (искусственных нейронов), связанных стрелками.
Электрические сигналы → числа
В реальной биологической нейронной сети от входов сети к выходам передается электрический сигнал. В процессе прохода по нейронной сети он может изменяться.
Электрический сигнал всегда будет электрическим сигналом. Концептуально ничего не изменяется. Но что же тогда меняется? Меняется величина этого электрического сигнала (сильнее/слабее). А любую величину всегда можно выразить числом (больше/меньше).
В нашей модели искусственной нейронной сети нам совершенно не нужно реализовывать поведение электрического сигнала, так как от его реализации все равно ничего зависеть не будет.
На входы сети мы будем подавать какие-то числа, символизирующие величины электрического сигнала, если бы он был. Эти числа будут продвигаться по сети и каким-то образом меняться. На выходе сети мы получим какое-то результирующее число, являющееся откликом сети.
Для удобства все равно будем называть наши числа, циркулирующие в сети, сигналами.
Синапсы → веса связей
Вспомним картинку из первой главы, на которой цветом были изображены связи между нейронами – синапсы. Синапсы могут усиливать или ослаблять проходящий по ним электрический сигнал.
Давайте характеризовать каждую такую связь определенным числом, называемым весом данной связи. Сигнал, прошедший через данную связь, умножается на вес соответствующей связи.
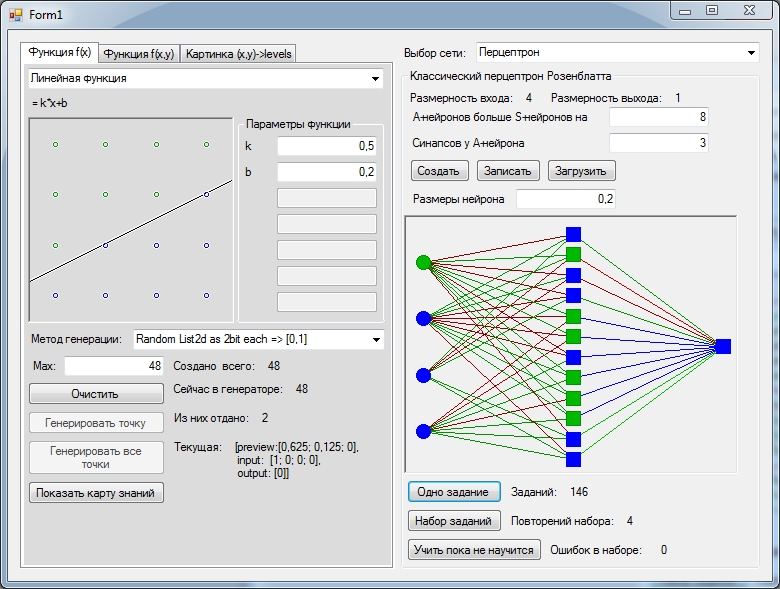
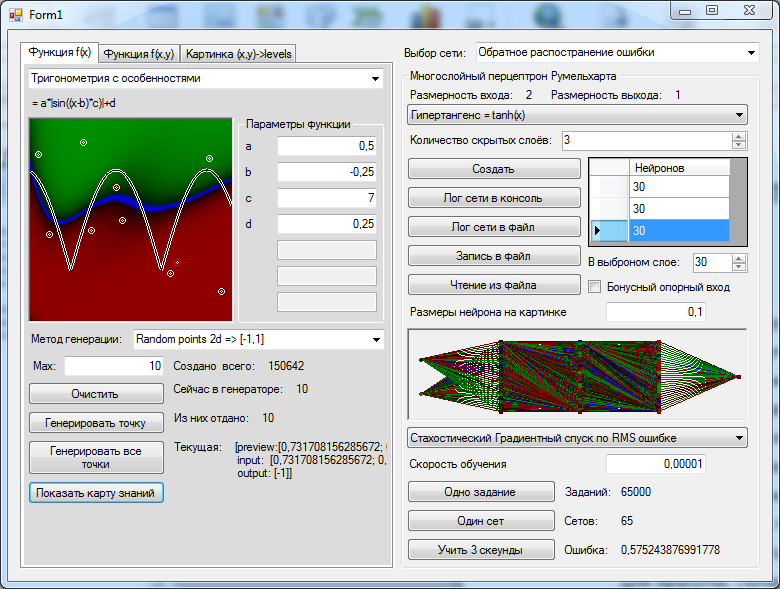
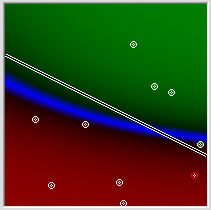
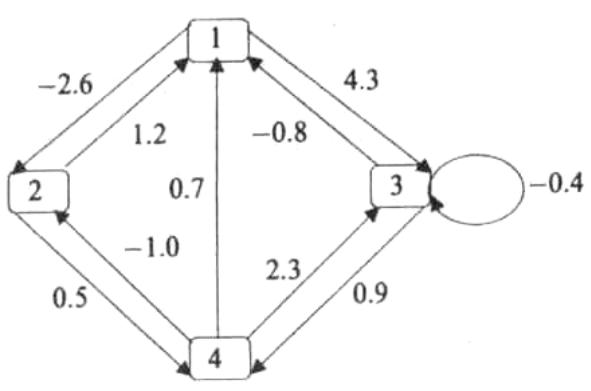
Это ключевой момент в концепции искусственных нейронных сетей, я объясню его подробнее. Посмотрите на картинку ниже. Теперь каждой черной стрелке (связи) на этой картинке соответствует некоторое число ( w_i ) (вес связи). И когда сигнал проходит по этой связи, его величина умножается на вес этой связи.
На приведенном выше рисунке вес стоит не у каждой связи лишь потому, что там нет места для обозначений. В реальности у каждой ( i )-ой связи свой собственный ( w_i )-ый вес.
Искусственный нейрон
Теперь мы переходим к рассмотрению внутренней структуры искусственного нейрона и того, как он преобразует поступающий на его входы сигнал.
На рисунке ниже представлена полная модель искусственного нейрона.
Не пугайтесь, ничего сложного здесь нет. Давайте рассмотрим все подробно слева направо.
Входы, веса и сумматор
У каждого нейрона, в том числе и у искусственного, должны быть какие-то входы, через которые он принимает сигнал. Мы уже вводили понятие весов, на которые умножаются сигналы, проходящие по связи. На картинке выше веса изображены кружками.
Поступившие на входы сигналы умножаются на свои веса. Сигнал первого входа ( x_1 ) умножается на соответствующий этому входу вес ( w_1 ). В итоге получаем ( x_1w_1 ). И так до ( n )-ого входа. В итоге на последнем входе получаем ( x_nw_n ).
Теперь все произведения передаются в сумматор. Уже исходя из его названия можно понять, что он делает. Он просто суммирует все входные сигналы, умноженные на соответствующие веса:
[ x_1w_1+x_2w_2+cdots+x_nw_n = sumlimits^n_{i=1}x_iw_i ]
Результатом работы сумматора является число, называемое взвешенной суммой.
Взвешенная сумма (Weighted sum) (( net )) — сумма входных сигналов, умноженных на соответствующие им веса.
[ net=sumlimits^n_{i=1}x_iw_i ]
Роль сумматора очевидна – он агрегирует все входные сигналы (которых может быть много) в какое-то одно число – взвешенную сумму, которая характеризует поступивший на нейрон сигнал в целом. Еще взвешенную сумму можно представить как степень общего возбуждения нейрона.
Пример
Для понимания роли последнего компонента искусственного нейрона – функции активации – я приведу аналогию.
Давайте рассмотрим один искусственный нейрон. Его задача – решить, ехать ли отдыхать на море. Для этого на его входы мы подаем различные данные. Пусть у нашего нейрона будет 4 входа:
- Стоимость поездки
- Какая на море погода
- Текущая обстановка с работой
- Будет ли на пляже закусочная
Все эти параметры будем характеризовать 0 или 1. Соответственно, если погода на море хорошая, то на этот вход подаем 1. И так со всеми остальными параметрами.
Если у нейрона есть четыре входа, то должно быть и четыре весовых коэффициента. В нашем примере весовые коэффициенты можно представить как показатели важности каждого входа, влияющие на общее решение нейрона. Веса входов распределим следующим образом:
- 5
- 4
- 1
- 1
Нетрудно заметить, что очень большую роль играют факторы стоимости и погоды на море (первые два входа). Они же и будут играть решающую роль при принятии нейроном решения.
Пусть на входы нашего нейрона мы подаем следующие сигналы:
- 1
- 0
- 0
- 1
Умножаем веса входов на сигналы соответствующих входов:
- 5
- 0
- 0
- 1
Взвешенная сумма для такого набора входных сигналов равна 6:
[ net=sumlimits^4_{i=1}x_iw_i = 5 + 0 + 0 + 1 =6 ]
Все классно, но что делать дальше? Как нейрон должен решить, ехать на море или нет? Очевидно, нам нужно как-то преобразовать нашу взвешенную сумму и получить ответ.
Вот на сцену выходит функция активации.
Функция активации
Просто так подавать взвешенную сумму на выход достаточно бессмысленно. Нейрон должен как-то обработать ее и сформировать адекватный выходной сигнал. Именно для этих целей и используют функцию активации.
Она преобразует взвешенную сумму в какое-то число, которое и является выходом нейрона (выход нейрона обозначим переменной ( out )).
Для разных типов искусственных нейронов используют самые разные функции активации. В общем случае их обозначают символом ( phi(net) ). Указание взвешенного сигнала в скобках означает, что функция активации принимает взвешенную сумму как параметр.
Функция активации (Activation function) (( phi(net) )) — функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона (( out )).
[ out=phi(net) ]
Далее мы подробно рассмотрим самые известные функции активации.
Функция единичного скачка
Самый простой вид функции активации. Выход нейрона может быть равен только 0 или 1. Если взвешенная сумма больше определенного порога ( b ), то выход нейрона равен 1. Если ниже, то 0.
Как ее можно использовать? Предположим, что мы поедем на море только тогда, когда взвешенная сумма больше или равна 5. Значит наш порог равен 5:
[ b=5 ]
В нашем примере взвешенная сумма равнялась 6, а значит выходной сигнал нашего нейрона равен 1. Итак, мы едем на море.
Однако если бы погода на море была бы плохой, а также поездка была бы очень дорогой, но имелась бы закусочная и обстановка с работой нормальная (входы: 0011), то взвешенная сумма равнялась бы 2, а значит выход нейрона равнялся бы 0. Итак, мы никуда не едем.
В общем, нейрон смотрит на взвешенную сумму и если она получается больше его порога, то нейрон выдает выходной сигнал, равный 1.
Графически эту функцию активации можно изобразить следующим образом.
На горизонтальной оси расположены величины взвешенной суммы. На вертикальной оси — значения выходного сигнала. Как легко видеть, возможны только два значения выходного сигнала: 0 или 1. Причем 0 будет выдаваться всегда от минус бесконечности и вплоть до некоторого значения взвешенной суммы, называемого порогом. Если взвешенная сумма равна порогу или больше него, то функция выдает 1. Все предельно просто.
Теперь запишем эту функцию активации математически. Почти наверняка вы сталкивались с таким понятием, как составная функция. Это когда мы под одной функцией объединяем несколько правил, по которым рассчитывается ее значение. В виде составной функции функция единичного скачка будет выглядеть следующим образом:
[ out(net) = begin{cases} 0, net < b 1, net geq b end{cases} ]
В этой записи нет ничего сложного. Выход нейрона (( out )) зависит от взвешенной суммы (( net )) следующим образом: если ( net ) (взвешенная сумма) меньше какого-то порога (( b )), то ( out ) (выход нейрона) равен 0. А если ( net ) больше или равен порогу ( b ), то ( out ) равен 1.
Сигмоидальная функция
На самом деле существует целое семейство сигмоидальных функций, некоторые из которых применяют в качестве функции активации в искусственных нейронах.
Все эти функции обладают некоторыми очень полезными свойствами, ради которых их и применяют в нейронных сетях. Эти свойства станут очевидными после того, как вы увидите графики этих функций.
Итак… самая часто используемая в нейронных сетях сигмоида — логистическая функция.
График этой функции выглядит достаточно просто. Если присмотреться, то можно увидеть некоторое подобие английской буквы ( S ), откуда и пошло название семейства этих функций.
А вот так она записывается аналитически:
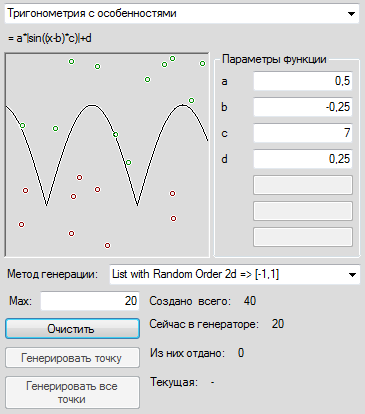
[ out(net)=frac{1}{1+exp(-a cdot net)} ]
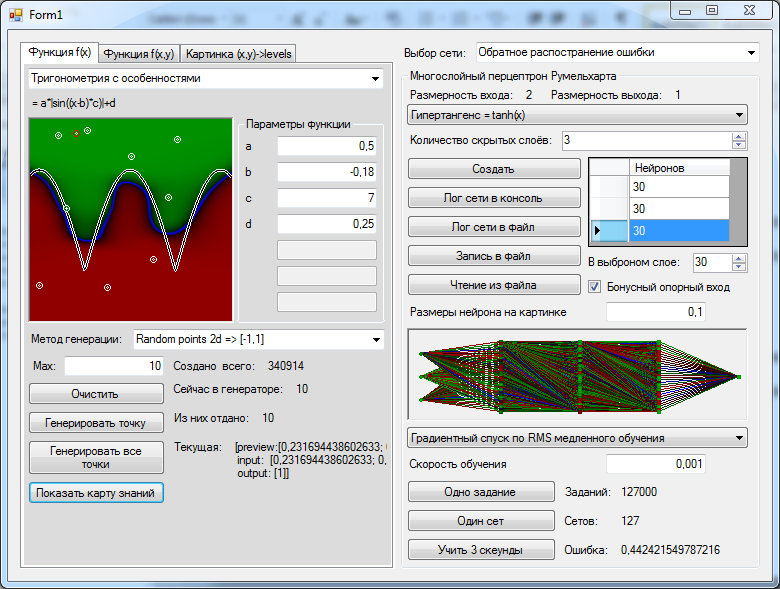
Что за параметр ( a )? Это какое-то число, которое характеризует степень крутизны функции. Ниже представлены логистические функции с разным параметром ( a ).
Вспомним наш искусственный нейрон, определяющий, надо ли ехать на море. В случае с функцией единичного скачка все было очевидно. Мы либо едем на море (1), либо нет (0).
Здесь же случай более приближенный к реальности. Мы до конца полностью не уверены (в особенности, если вы параноик) – стоит ли ехать? Тогда использование логистической функции в качестве функции активации приведет к тому, что вы будете получать цифру между 0 и 1. Причем чем больше взвешенная сумма, тем ближе выход будет к 1 (но никогда не будет точно ей равен). И наоборот, чем меньше взвешенная сумма, тем ближе выход нейрона будет к 0.
Например, выход нашего нейрона равен 0.8. Это значит, что он считает, что поехать на море все-таки стоит. Если бы его выход был бы равен 0.2, то это означает, что он почти наверняка против поездки на море.
Какие же замечательные свойства имеет логистическая функция?
- она является «сжимающей» функцией, то есть вне зависимости от аргумента (взвешенной суммы), выходной сигнал всегда будет в пределах от 0 до 1
- она более гибкая, чем функция единичного скачка – ее результатом может быть не только 0 и 1, но и любое число между ними
- во всех точках она имеет производную, и эта производная может быть выражена через эту же функцию
Именно из-за этих свойств логистическая функция чаще всего используются в качестве функции активации в искусственных нейронах.
Гиперболический тангенс
Однако есть и еще одна сигмоида – гиперболический тангенс. Он применяется в качестве функции активации биологами для более реалистичной модели нервной клетки.
Такая функция позволяет получить на выходе значения разных знаков (например, от -1 до 1), что может быть полезным для ряда сетей.
Функция записывается следующим образом:
[ out(net) = tanhleft(frac{net}{a}right) ]
В данной выше формуле параметр ( a ) также определяет степень крутизны графика этой функции.
А вот так выглядит график этой функции.
Как видите, он похож на график логистической функции. Гиперболический тангенс обладает всеми полезными свойствами, которые имеет и логистическая функция.
Что мы узнали?
Теперь вы получили полное представление о внутренней структуре искусственного нейрона. Я еще раз приведу краткое описание его работы.
У нейрона есть входы. На них подаются сигналы в виде чисел. Каждый вход имеет свой вес (тоже число). Сигналы на входе умножаются на соответствующие веса. Получаем набор «взвешенных» входных сигналов.
Далее этот набор попадает в сумматор, которой просто складывает все входные сигналы, помноженные на веса. Получившееся число называют взвешенной суммой.
Затем взвешенная сумма преобразуется функцией активации и мы получаем выход нейрона.
Сформулируем теперь самое короткое описание работы нейрона – его математическую модель:
Математическая модель искусственного нейрона с ( n ) входами:
[ out=phileft(sumlimits^n_{i=1}x_iw_iright) ]
где
( phi ) – функция активации
( sumlimits^n_{i=1}x_iw_i ) – взвешенная сумма, как сумма ( n ) произведений входных сигналов на соответствующие веса.
Виды ИНС
Мы разобрались со структурой искусственного нейрона. Искусственные нейронные сети состоят из совокупности искусственных нейронов. Возникает логичный вопрос – а как располагать/соединять друг с другом эти самые искусственные нейроны?
Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу – распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений.
А дальше начинаются различия…
Однослойные нейронные сети
В однослойных нейронных сетях сигналы с входного слоя сразу подаются на выходной слой. Он производит необходимые вычисления, результаты которых сразу подаются на выходы.
Выглядит однослойная нейронная сеть следующим образом:
На этой картинке входной слой обозначен кружками (он не считается за слой нейронной сети), а справа расположен слой обычных нейронов.
Нейроны соединены друг с другом стрелками. Над стрелками расположены веса соответствующих связей (весовые коэффициенты).
Однослойная нейронная сеть (Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.
Многослойные нейронные сети
Такие сети, помимо входного и выходного слоев нейронов, характеризуются еще и скрытым слоем (слоями). Понять их расположение просто – эти слои находятся между входным и выходным слоями.
Такая структура нейронных сетей копирует многослойную структуру определенных отделов мозга.
Название скрытый слой получил неслучайно. Дело в том, что только относительно недавно были разработаны методы обучения нейронов скрытого слоя. До этого обходились только однослойными нейросетями.
Многослойные нейронные сети обладают гораздо большими возможностями, чем однослойные.
Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.
Многослойная нейронная сеть (Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.
Сети прямого распространения
Можно заметить одну очень интересную деталь на картинках нейросетей в примерах выше.
Во всех примерах стрелки строго идут слева направо, то есть сигнал в таких сетях идет строго от входного слоя к выходному.
Сети прямого распространения (Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.
Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.
Однако никто не запрещает сигналу идти и в обратную сторону.
Сети с обратными связями
В сетях такого типа сигнал может идти и в обратную сторону. В чем преимущество?
Дело в том, что в сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах.
А в сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).
Возможность сигналов циркулировать в сети открывает новые, удивительные возможности нейронных сетей. С помощью таких сетей можно создавать нейросети, восстанавливающие или дополняющие сигналы. Другими словами такие нейросети имеют свойства кратковременной памяти (как у человека).
Сети с обратными связями (Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.
Обучение нейронной сети
Теперь давайте чуть более подробно рассмотрим вопрос обучения нейронной сети. Что это такое? И каким образом это происходит?
Что такое обучение сети?
Искусственная нейронная сеть – это совокупность искусственных нейронов. Теперь давайте возьмем, например, 100 нейронов и соединим их друг с другом. Ясно, что при подаче сигнала на вход, мы получим что-то бессмысленное на выходе.
Значит нам надо менять какие-то параметры сети до тех пор, пока входной сигнал не преобразуется в нужный нам выходной.
Что мы можем менять в нейронной сети?
Изменять общее количество искусственных нейронов бессмысленно по двум причинам. Во-первых, увеличение количества вычислительных элементов в целом лишь делает систему тяжеловеснее и избыточнее. Во-вторых, если вы соберете 1000 дураков вместо 100, то они все-равно не смогут правильно ответить на вопрос.
Сумматор изменить не получится, так как он выполняет одну жестко заданную функцию – складывать. Если мы его заменим на что-то или вообще уберем, то это вообще уже не будет искусственным нейроном.
Если менять у каждого нейрона функцию активации, то мы получим слишком разношерстную и неконтролируемую нейронную сеть. К тому же, в большинстве случаев нейроны в нейронных сетях одного типа. То есть они все имеют одну и ту же функцию активации.
Остается только один вариант – менять веса связей.
Обучение нейронной сети (Training) — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Такой подход к термину «обучение нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей. Каждая из них в отдельности состоит из нейронов одного типа (функция активации одинаковая). Мы обучаемся благодаря изменению синапсов – элементов, которые усиливают/ослабляют входной сигнал.
Однако есть еще один важный момент. Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ». Со стороны будет казаться, что она очень быстро «обучилась». И как только вы подадите немного измененный сигнал, ожидая увидеть правильный ответ, то сеть выдаст бессмыслицу.
В самом деле, зачем нам сеть, определяющая лицо только на одном фото. Мы ждем от сети способности обобщать какие-то признаки и узнавать лица и на других фотографиях тоже.
Именно с этой целью и создаются обучающие выборки.
Обучающая выборка (Training set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике.
Однако прежде чем пускать свежеиспеченную нейросеть в бой, часто производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка (Testing set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Мы поняли, что такое «обучение сети» – подбор правильного набора весов. Теперь возникает вопрос – а как можно обучать сеть? В самом общем случае есть два подхода, приводящие к разным результатам: обучение с учителем и обучение без учителя.
Обучение с учителем
Суть данного подхода заключается в том, что вы даете на вход сигнал, смотрите на ответ сети, а затем сравниваете его с уже готовым, правильным ответом.
Важный момент. Не путайте правильные ответы и известный алгоритм решения! Вы можете обвести пальцем лицо на фото (правильный ответ), но не сможете сказать, как это сделали (известный алгоритм). Тут такая же ситуация.
Затем, с помощью специальных алгоритмов, вы меняете веса связей нейронной сети и снова даете ей входной сигнал. Сравниваете ее ответ с правильным и повторяете этот процесс до тех пор, пока сеть не начнет отвечать с приемлемой точностью (как я говорил в 1 главе, однозначно точных ответов сеть давать не может).
Обучение с учителем (Supervised learning) — вид обучения сети, при котором ее веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
Где взять правильные ответы?
Если мы хотим, чтобы сеть узнавала лица, мы можем создать обучающую выборку на 1000 фотографий (входные сигналы) и самостоятельно выделить на ней лица (правильные ответы).
Если мы хотим, чтобы сеть прогнозировала рост/падение цен, то обучающую выборку надо делать, основываясь на прошлых данных. В качестве входных сигналов можно брать определенные дни, общее состояние рынка и другие параметры. А в качестве правильных ответов – рост и падение цены в те дни.
И так далее…
Стоит отметить, что учитель, конечно же, не обязательно человек. Дело в том, что порой сеть приходится тренировать часами и днями, совершая тысячи и десятки тысяч попыток. В 99% случаев эту роль выполняет компьютер, а точнее, специальная компьютерная программа.
Обучение без учителя
Обучение без учителя применяют тогда, когда у нас нет правильных ответов на входные сигналы. В этом случае вся обучающая выборка состоит из набора входных сигналов.
Что же происходит при таком обучении сети? Оказывается, что при таком «обучении» сеть начинает выделять классы подаваемых на вход сигналов. Короче говоря – сеть начинает кластеризацию.
Например, вы демонстрируете сети конфеты, пирожные и торты. Вы никак не регулируете работу сети. Вы просто подаете на ее входы данные о данном объекте. Со временем сеть начнет выдавать сигналы трех разных типов, которые и отвечают за объекты на входе.
Обучение без учителя (Unsupervised learning) — вид обучения сети, при котором сеть самостоятельно классифицирует входные сигналы. Правильные (эталонные) выходные сигналы не демонстрируются.
Выводы
В этой главе вы узнали все о структуре искусственного нейрона, а также получили полное представление о том, как он работает (и о его математической модели).
Более того, вы теперь знаете о различных видах искусственных нейронных сетей: однослойные, многослойные, а также feedforward сети и сети с обратными связями.
Вы также ознакомились с тем, что представляет собой обучение сети с учителем и без учителя.
Вы уже знаете необходимую теорию. Последующие главы – рассмотрение конкретных видов нейронных сетей, конкретные алгоритмы их обучения и практика программирования.
Вопросы и задачи
Материал этой главы надо знать очень хорошо, так как в ней содержатся основные теоретические сведения по искусственным нейронным сетям. Обязательно добейтесь уверенных и правильных ответов на все нижеприведенные вопросы и задачи.
Опишите упрощения ИНС по сравнению с биологическими нейросетями.
Из каких элементов состоит искусственный нейрон?
Что такое взвешенная сумма? Какой компонент искусственного нейрона ее вычисляет?
Вычислите взвешенную сумму нейрона (рисунок выше)
Что такое функция активации?
Запишите математическую модель искусственного нейрона.
Чем отличаются однослойные и многослойные нейронные сети?
В чем отличие feedforward сетей от сетей с обратными связями?
Что такое обучающая выборка? В чем ее смысл?
Что понимают под обучением сети?
Что такое обучение с учителем и без него?
В теле человека бессчетное количество клеток, каждая из которых имеет собственную функцию. Среди них самые загадочные – нейроны, отвечающие за любое совершаемое нами действие. Попробуем разобраться как работают нейроны и в чем их предназначение.
Что такое нейрон (нейронные связи)
В переводе с греческого нейрон, или как его еще называют неврон, означает «волокно», «нерв». Нейрон – это специфическая структура в нашем организме, которая отвечает за передачу внутри него любой информации, в быту называемая нервной клеткой.
Нейроны работают при помощи электрических сигналов и способствуют обработке мозгом поступающей информации для дальнейшей координации производимых телом действий.
Эти клетки являются составляющей частью нервной системы человека, предназначение которой состоит в том, чтобы собрать все сигналы, поступающие из вне или от собственного организма и принять решение о необходимости того или иного действия. Именно нейроны помогают справиться с такой задачей.
Каждый из нейронов имеет связь с огромным количеством таких же клеток, создаётся своеобразная «паутина», которая называется нейронной сетью. Посредством данной связи в организме передаются электрические и химические импульсы, приводящие всю нервную систему в состояние покоя либо, наоборот, возбуждения.
К примеру, человек столкнулся с неким значимым событием. Возникает электрохимический толчок (импульс) нейронов, приводящий к возбуждению неровной системы. У человека начинает чаще биться сердце, потеют руки или возникают другие физиологические реакции.
Мы рождаемся с заданным количеством нейронов, но связи между ними еще не сформированы. Нейронная сеть строится постепенно в результате поступающих из вне импульсов. Новые толчки формируют новые нейронные пути, именно по ним в течение жизни побежит аналогичная информация. Мозг воспринимает индивидуальный опыт каждого человека и реагирует на него. К примеру, ребенок, схватился за горячий утюг и отдернул руку. Так у него появилась новая нейронная связь.
Стабильная нейронная сеть выстраивается у ребенка уже к двум годам. Удивительно, но уже с этого возраста те клетки, которые не используются, начинают ослабевать. Но это никак не мешает развитию интеллекта. Наоборот, ребенок познает мир через уже устоявшиеся нейронные связи, а не анализирует бесцельно все вокруг.
Даже у такого малыша есть практический опыт, позволяющий отсекать ненужные действия и стремиться к полезным. Поэтому, например, так сложно отучить ребенка от груди — у него сформировалась крепкая нейронная связь между приложением к материнскому молоку и удовольствию, безопасности, спокойствию.
Познание нового опыта на протяжении всей жизни приводит к отмиранию ненужных нейронных связей и формированию новых и полезных. Этот процесс оптимизирует головной мозг наиболее эффективным для нас образом. Например, люди, проживающие в жарких странах, учатся жить в определенном климате, а северянам нужен совсем другой опыт для выживания.
Сколько нейронов в мозге
Нервные клетки в составе головного мозга занимают порядка 10 процентов, остальные 90 процентов это астроциты и глиальные клетки, но их задача заключается лишь в обслуживании нейронов.
Подсчитать «вручную» численность клеток в головном мозге также сложно, как узнать количество звезд на небе.
Тем не менее ученые придумали сразу несколько способов для определения количества нейронов у человека:
- Рассчитывается число нервных клеток на небольшой части мозга, а затем, количество умножается пропорционально полному объему. Исследователи исходят из постулата о том, что нейроны равномерно распределены в нашем мозге.
- Происходит растворение всех мозговых клеток. В результате получается жидкость, в составе которой можно увидеть клеточные ядра. Их можно посчитать. При этом служебные клетки, о которых мы сказали выше, не учитываются.
В результате описанных экспериментов установлено, что число нейронов в головном мозге человека — 85 миллиардов единиц. Ранее, на протяжении многих веков считалось, что нервных клеток больше, порядка 100 миллиардов.
Строение нейрона
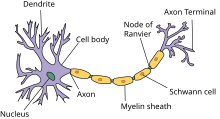
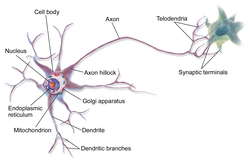
На рисунке приведено строение нейрона. Он состоит из основного тела и ядра. От клеточного тела идет ответвление многочисленных волокон, которые именуются дендритами.
Мощные и длинные дендриты называются аксонами, которые в действительности намного длиннее, чем на картинке. Их протяженность варьируется от нескольких миллиметров до более метра.
Аксоны играют ведущую роль в передаче информации между нейронами и обеспечивают работу всей нервной системы.
Место соединения дендрита (аксона) с другим нейроном называется синапсом. Дендриты при наличии раздражителей могут разрастись настолько сильно, что станут улавливать импульсы от других клеток, что приводит к образованию новых синаптических связей.
Синаптические связи играют существенную роль в формировании личности человека. Так, личность с устоявшимся позитивным опытом будет смотреть на жизнь с любовью и надеждой, человек, у которого нейронные связи с негативным зарядом, станет со временем пессимистом.
Виды нейронов и нейронных связей
Нейроны можно обнаружить в различных органах человека, а не исключительно в головном мозге. Большое их количество расположено в рецепторах (глаза, уши, язык, пальцы рук – органы чувств). Совокупность нервных клеток, которые пронизывают наш организм составляет основу периферической нервной системы. Выделим основные виды нейронов.
| Вид нейронной клетки | За что отвечает |
|---|---|
| Аффекторные | Являются переносчиками информации от органов чувств в головной мозг. У этого вида нейронов самые длинные аксоны. Импульс из вне поступает по аксонам строго в определенный участок головного мозга, звук — в слуховой «отсек», запах – в «обонятельный» и т.д. |
| Промежуточные | Промежуточные нервные клетки обрабатывают сведения, поступившие от аффекторных нейронов и передают ее периферическим органам и мышцам. |
| Эффекторные | На заключительном этапе в дело вступают эфференты, которые доводят команду промежуточных нейронов до мышц и других органов тела. |
Слаженная работа нейронов трех типов выглядит так: человек «слышит» запах шашлыка, нейрон передает информацию в соответствующий раздел мозга, мозг передает сигнал желудку, который выделяет желудочный сок, человек принимает решение «хочу есть» и бежит покупать шашлык. Упрощенно так это действует.
Самыми загадочными являются промежуточные нейроны. С одной стороны, их работа обуславливает наличие рефлекса: дотронулся до электричества – отдернул руку, полетела пыль –зажмурился. Однако, пока не объяснимо как обмен между волокнами рождает идеи, образы, мысли?
Единственное, что установили ученые, это тот факт, что любой вид мыслительной деятельности (чтение книг, рисование, решение математических задач) сопровождается особой активностью (вспышкой) нервных клеток определенного участка головного мозга.
Есть особая разновидность нейронов, которые именуются зеркальными. Их особенность заключается в том, что они не только приходят в возбуждение от внешних сигналов, но и начинают «шевелиться», наблюдая за действиями своих собратьев – других нейронов.
Функции нейронов
Без нейронов невозможна работа организма человека. Мы увидели, что эти наноклетки отвечают буквально за каждое наше движение, любой поступок. Выполняемые ими функции до настоящего времени в полной мере не изучены и не определены.
Существует несколько классификаций функций нейронов. Мы остановимся на общепринятой в научном мире.
Функция распространения информации
Данная функция:
- является основной;
- изучена лучше остальных.
Суть ее в том, что нейронами обрабатываются и переносятся в головной мозг все импульсы, которые поступают из окружающего мира или собственного тела. Далее происходит их обработка, подобно тому, как работает поисковик в браузере.
По результатам сканирования сведений из вне, головной мозг в форме обратной связи передает обработанную информацию к органам чувств или мышцам.
Мы не подозреваем, что в нашем теле происходит ежесекундная доставка и переработка информации, не только в голове и на уровне периферической нервной системы.
До настоящего времени создать искусственный интеллект, который бы приблизился к работе нейронных сетей человека, не удалось. У каждого из 85 миллиардов нейронов имеется, как минимум, 10 тысяч обусловленных опытом связей, и все они работают на передачу и обработку информации.
Функция аккумуляции знаний (сохранения опыта)
Человек обладает памятью, возможностью понимать суть вещей, явлений и действий, которые он единожды или многократно повторял. За формирование памяти отвечают именно нейронные клетки, точнее нейротрансмиттеры, связующие звенья между соседними нейронами.
Таким образом, за память отвечает не какая-то отдельная часть мозга, а маленькие белковые мостики между клетками. Человек может потерять память, когда произошло крушение этих нервных связей.
Функция интеграции
Данная функция позволяет взаимодействовать между собой отдельным долям головного мозга. Как мы уже сказали, сигналы от разных органов чувств поступают в разные отделы мозга.
Нейроны посредством «вспышек» активности передают и принимают импульсы в разных частях мозга. Так происходит процесс появления мыслей, эмоций и чувств. Чем больше таких разноплановых связей, тем эффективнее человек мыслит. Если человек способен к размышлениям и аналитике в определенном направлении, то он будет хорошо соображать и в другом вопросе.
Функция производства белков
Нейроны – настолько полезные клетки, что не ограничиваются только передаточными функциями. Нервные клетки вырабатывают необходимые для жизни человека белки. Опять же ключевую роль в производстве белков имеют нейротрансмиттеры, которые отвечают за память.
Всего в невронах индуцируется порядка 80 белков, вот основные из них, влияющие на самочувствие человека:
- Серотонин – вещество, вызывающее радость и удовольствие.
- Допамин – ведущий источник бодрости и счастья для человека. Активизирует физическую активность, помогает проснуться, переизбыток может привести к состоянию эйфории.
- Норадреналин – это «плохой» гормон, вызывающий приступы ярости и гнева. Наряду с кортизолом его называют гормоном стресса.
- Глутамат – вещество, отвечающие за хранение памяти.
Прекращение выработки белков или их выпуск в недостаточном количестве способны привести к тяжелым заболеваниям.
Восстанавливаются ли нервные клетки
При нормальном состоянии организма нейроны могут жить и функционировать очень долго. К сожалению, случается так, что они начинают массово погибать. Причин разрушения нервных волокон может быть много, но до конца механизм их деструкции не изучен.
Установлено, что нервные клетки погибают из-за гипоксии (кислородное голодание). Нейронные сети рушатся при отдельных травмах головного мозга, человек теряет память или утрачивает способность к хранению информации. В этом случае сами нейроны сохранены, но теряется их передаточная функция.
Отсутствие допамина ведет к развитию болезни Паркинсона, а его переизбыток является причиной шизофрении. Почему прекращается выработка белка не известно, спусковой механизм не выявлен.
Гибель нервных клеток происходит при алкоголизации личности. Алкоголик со временем может совершенно деградировать и утратить вкус к жизни.
Формирование нервных клеток происходит при рождении. Долгое время ученые полагали, что со временем нейроны отмирают. Поэтому с возрастом человек утрачивает способность накапливать информацию, хуже соображает. Нарушение функции по выработке допамина и серотонина связывается с наличием практически у всех пожилых людей депрессивных состояний.
Гибель нейронов, действительно неизбежна, в год исчезает примерно 1 процент от их количества. Но есть и хорошие новости. Последние исследования показали, что в коре головного мозга есть особенный участок, именуемый гипокаммом. Именно в нем генерируются новые чистые нейроны. Подсчитано примерное количество генерируемых ежедневно нервных клеток – 1400.
В науке обозначилось новое понятие «нейропластичность», обозначающее возможность мозга регенерироваться и перестраиваться. Но есть одна тонкость: новые нейроны еще не имеют никакого опыта и наработанных связей. Поэтому с возрастом или после заболевания мозг нужно тренировать, как и все иные мышцы тела: получать новые знания, анализировать происходящие события и явления.
Подобно тому, как мы усиливаем бицепс при помощи гантели, активизировать процесс включения новых нервных клеток можно следующими способами:
- изучение новых сфер знаний, которые ранее были не нужны или не интересны. К примеру, математику можно начать изучать живопись, а юристу – основы физики.
- через постановку сложных задач и поиск их решения;
- составлением планов деятельности, которые включают в себя множество исходных данных.
Механизм возрождения прост. У нас имеются совершенно не задействованные новые клетки, которые нужно заставить работать, а сделать это можно лишь путем постановки новых задач и изучения неизвестных предметных сфер.
Вся информация взята из открытых источников.
Если вы считаете, что ваши авторские права нарушены, пожалуйста,
напишите в чате на этом сайте, приложив скан документа подтверждающего ваше право.
Мы убедимся в этом и сразу снимем публикацию.
| Axon | |
|---|---|
An axon of a multipolar neuron |
|
| Identifiers | |
| MeSH | D001369 |
| FMA | 67308 |
| Anatomical terminology
[edit on Wikidata] |
An axon (from Greek ἄξων áxōn, axis), or nerve fiber (or nerve fibre: see spelling differences), is a long, slender projection of a nerve cell, or neuron, in vertebrates, that typically conducts electrical impulses known as action potentials away from the nerve cell body. The function of the axon is to transmit information to different neurons, muscles, and glands. In certain sensory neurons (pseudounipolar neurons), such as those for touch and warmth, the axons are called afferent nerve fibers and the electrical impulse travels along these from the periphery to the cell body and from the cell body to the spinal cord along another branch of the same axon. Axon dysfunction can be the cause of many inherited and acquired neurological disorders that affect both the peripheral and central neurons. Nerve fibers are classed into three types – group A nerve fibers, group B nerve fibers, and group C nerve fibers. Groups A and B are myelinated, and group C are unmyelinated. These groups include both sensory fibers and motor fibers. Another classification groups only the sensory fibers as Type I, Type II, Type III, and Type IV.
An axon is one of two types of cytoplasmic protrusions from the cell body of a neuron; the other type is a dendrite. Axons are distinguished from dendrites by several features, including shape (dendrites often taper while axons usually maintain a constant radius), length (dendrites are restricted to a small region around the cell body while axons can be much longer), and function (dendrites receive signals whereas axons transmit them). Some types of neurons have no axon and transmit signals from their dendrites. In some species, axons can emanate from dendrites known as axon-carrying dendrites.[1] No neuron ever has more than one axon; however in invertebrates such as insects or leeches the axon sometimes consists of several regions that function more or less independently of each other.[2]
Axons are covered by a membrane known as an axolemma; the cytoplasm of an axon is called axoplasm. Most axons branch, in some cases very profusely. The end branches of an axon are called telodendria. The swollen end of a telodendron is known as the axon terminal which joins the dendron or cell body of another neuron forming a synaptic connection. Axons make contact with other cells – usually other neurons but sometimes muscle or gland cells – at junctions called synapses. In some circumstances, the axon of one neuron may form a synapse with the dendrites of the same neuron, resulting in an autapse. At a synapse, the membrane of the axon closely adjoins the membrane of the target cell, and special molecular structures serve to transmit electrical or electrochemical signals across the gap. Some synaptic junctions appear along the length of an axon as it extends; these are called en passant («in passing») synapses and can be in the hundreds or even the thousands along one axon.[3] Other synapses appear as terminals at the ends of axonal branches.
A single axon, with all its branches taken together, can innervate multiple parts of the brain and generate thousands of synaptic terminals. A bundle of axons make a nerve tract in the central nervous system,[4] and a fascicle in the peripheral nervous system. In placental mammals the largest white matter tract in the brain is the corpus callosum, formed of some 200 million axons in the human brain.[4]
Anatomy[edit]
A typical myelinated axon
Axons are the primary transmission lines of the nervous system, and as bundles they form nerves. Some axons can extend up to one meter or more while others extend as little as one millimeter. The longest axons in the human body are those of the sciatic nerve, which run from the base of the spinal cord to the big toe of each foot. The diameter of axons is also variable. Most individual axons are microscopic in diameter (typically about one micrometer (µm) across). The largest mammalian axons can reach a diameter of up to 20 µm. The squid giant axon, which is specialized to conduct signals very rapidly, is close to 1 millimeter in diameter, the size of a small pencil lead. The numbers of axonal telodendria (the branching structures at the end of the axon) can also differ from one nerve fiber to the next. Axons in the central nervous system (CNS) typically show multiple telodendria, with many synaptic end points. In comparison, the cerebellar granule cell axon is characterized by a single T-shaped branch node from which two parallel fibers extend. Elaborate branching allows for the simultaneous transmission of messages to a large number of target neurons within a single region of the brain.
There are two types of axons in the nervous system: myelinated and unmyelinated axons.[5] Myelin is a layer of a fatty insulating substance, which is formed by two types of glial cells: Schwann cells and oligodendrocytes. In the peripheral nervous system Schwann cells form the myelin sheath of a myelinated axon. Oligodendrocytes form the insulating myelin in the CNS. Along myelinated nerve fibers, gaps in the myelin sheath known as nodes of Ranvier occur at evenly spaced intervals. The myelination enables an especially rapid mode of electrical impulse propagation called saltatory conduction.
The myelinated axons from the cortical neurons form the bulk of the neural tissue called white matter in the brain. The myelin gives the white appearance to the tissue in contrast to the grey matter of the cerebral cortex which contains the neuronal cell bodies. A similar arrangement is seen in the cerebellum. Bundles of myelinated axons make up the nerve tracts in the CNS. Where these tracts cross the midline of the brain to connect opposite regions they are called commissures. The largest of these is the corpus callosum that connects the two cerebral hemispheres, and this has around 20 million axons.[4]
The structure of a neuron is seen to consist of two separate functional regions, or compartments – the cell body together with the dendrites as one region, and the axonal region as the other.
Axonal region[edit]
The axonal region or compartment, includes the axon hillock, the initial segment, the rest of the axon, and the axon telodendria, and axon terminals. It also includes the myelin sheath. The Nissl bodies that produce the neuronal proteins are absent in the axonal region.[3] Proteins needed for the growth of the axon, and the removal of waste materials, need a framework for transport. This axonal transport is provided for in the axoplasm by arrangements of microtubules and intermediate filaments known as neurofilaments.
Axon hillock[edit]
Detail showing microtubules at axon hillock and initial segment.
The axon hillock is the area formed from the cell body of the neuron as it extends to become the axon. It precedes the initial segment. The received action potentials that are summed in the neuron are transmitted to the axon hillock for the generation of an action potential from the initial segment.
Axonal initial segment[edit]
The axonal initial segment (AIS) is a structurally and functionally separate microdomain of the axon.[6][7] One function of the initial segment is to separate the main part of an axon from the rest of the neuron; another function is to help initiate action potentials.[8] Both of these functions support neuron cell polarity, in which dendrites (and, in some cases the soma) of a neuron receive input signals at the basal region, and at the apical region the neuron’s axon provides output signals.[9]
The axon initial segment is unmyelinated and contains a specialized complex of proteins. It is between approximately 20 and 60 µm in length and functions as the site of action potential initiation.[10][11] Both the position on the axon and the length of the AIS can change showing a degree of plasticity that can fine-tune the neuronal output.[10][12] A longer AIS is associated with a greater excitability.[12] Plasticity is also seen in the ability of the AIS to change its distribution and to maintain the activity of neural circuitry at a constant level.[13]
The AIS is highly specialized for the fast conduction of nerve impulses. This is achieved by a high concentration of voltage-gated sodium channels in the initial segment where the action potential is initiated.[13] The ion channels are accompanied by a high number of cell adhesion molecules and scaffolding proteins that anchor them to the cytoskeleton.[10] Interactions with ankyrin G are important as it is the major organizer in the AIS.[10]
Axonal transport[edit]
The axoplasm is the equivalent of cytoplasm in the cell. Microtubules form in the axoplasm at the axon hillock. They are arranged along the length of the axon, in overlapping sections, and all point in the same direction – towards the axon terminals.[14] This is noted by the positive endings of the microtubules. This overlapping arrangement provides the routes for the transport of different materials from the cell body.[14] Studies on the axoplasm has shown the movement of numerous vesicles of all sizes to be seen along cytoskeletal filaments – the microtubules, and neurofilaments, in both directions between the axon and its terminals and the cell body.
Outgoing anterograde transport from the cell body along the axon, carries mitochondria and membrane proteins needed for growth to the axon terminal. Ingoing retrograde transport carries cell waste materials from the axon terminal to the cell body.[15] Outgoing and ingoing tracks use different sets of motor proteins.[14] Outgoing transport is provided by kinesin, and ingoing return traffic is provided by dynein. Dynein is minus-end directed.[15] There are many forms of kinesin and dynein motor proteins, and each is thought to carry a different cargo.[14] The studies on transport in the axon led to the naming of kinesin.[14]
Myelination[edit]
TEM of a myelinated axon in cross-section.
In the nervous system, axons may be myelinated, or unmyelinated. This is the provision of an insulating layer, called a myelin sheath. The myelin membrane is unique in its relatively high lipid to protein ratio.[16]
In the peripheral nervous system axons are myelinated by glial cells known as Schwann cells. In the central nervous system the myelin sheath is provided by another type of glial cell, the oligodendrocyte. Schwann cells myelinate a single axon. An oligodendrocyte can myelinate up to 50 axons.[17]
The composition of myelin is different in the two types. In the CNS the major myelin protein is proteolipid protein, and in the PNS it is myelin basic protein.
Nodes of Ranvier[edit]
Nodes of Ranvier (also known as myelin sheath gaps) are short unmyelinated segments of a myelinated axon, which are found periodically interspersed between segments of the myelin sheath. Therefore, at the point of the node of Ranvier, the axon is reduced in diameter.[18] These nodes are areas where action potentials can be generated. In saltatory conduction, electrical currents produced at each node of Ranvier are conducted with little attenuation to the next node in line, where they remain strong enough to generate another action potential. Thus in a myelinated axon, action potentials effectively «jump» from node to node, bypassing the myelinated stretches in between, resulting in a propagation speed much faster than even the fastest unmyelinated axon can sustain.
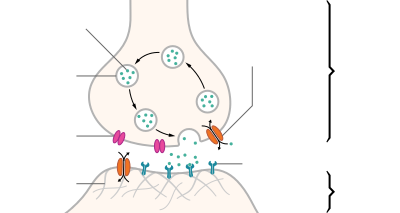
Axon terminals[edit]
An axon can divide into many branches called telodendria (Greek for ‘end of tree’). At the end of each telodendron is an axon terminal (also called a synaptic bouton, or terminal bouton). Axon terminals contain synaptic vesicles that store the neurotransmitter for release at the synapse. This makes multiple synaptic connections with other neurons possible. Sometimes the axon of a neuron may synapse onto dendrites of the same neuron, when it is known as an autapse.
Action potentials[edit]
| Structure of a typical chemical synapse |
|---|
|
Postsynaptic Voltage- Synaptic Neurotransmitter Receptor Neurotransmitter Axon terminal Synaptic cleft Dendrite |
Most axons carry signals in the form of action potentials, which are discrete electrochemical impulses that travel rapidly along an axon, starting at the cell body and terminating at points where the axon makes synaptic contact with target cells. The defining characteristic of an action potential is that it is «all-or-nothing» – every action potential that an axon generates has essentially the same size and shape. This all-or-nothing characteristic allows action potentials to be transmitted from one end of a long axon to the other without any reduction in size. There are, however, some types of neurons with short axons that carry graded electrochemical signals, of variable amplitude.
When an action potential reaches a presynaptic terminal, it activates the synaptic transmission process. The first step is rapid opening of calcium ion channels in the membrane of the axon, allowing calcium ions to flow inward across the membrane. The resulting increase in intracellular calcium concentration causes synaptic vesicles (tiny containers enclosed by a lipid membrane) filled with a neurotransmitter chemical to fuse with the axon’s membrane and empty their contents into the extracellular space. The neurotransmitter is released from the presynaptic nerve through exocytosis. The neurotransmitter chemical then diffuses across to receptors located on the membrane of the target cell. The neurotransmitter binds to these receptors and activates them. Depending on the type of receptors that are activated, the effect on the target cell can be to excite the target cell, inhibit it, or alter its metabolism in some way. This entire sequence of events often takes place in less than a thousandth of a second. Afterward, inside the presynaptic terminal, a new set of vesicles is moved into position next to the membrane, ready to be released when the next action potential arrives. The action potential is the final electrical step in the integration of synaptic messages at the scale of the neuron.[5]
(A) pyramidal cell, interneuron, and short durationwaveform (Axon), overlay of the three average waveforms;
(B) Average and standard error of peak-trough time for pyramidal cells interneurons, and putative axons;
(C) Scatter plot of signal to noise ratios for individual units againstpeak-trough time for axons, pyramidal cells (PYR) and interneurons (INT).
Extracellular recordings of action potential propagation in axons has been demonstrated in freely moving animals. While extracellular somatic action potentials have been used to study cellular activity in freely moving animals such as place cells, axonal activity in both white and gray matter can also be recorded. Extracellular recordings of axon action potential propagation is distinct from somatic action potentials in three ways: 1. The signal has a shorter peak-trough duration (~150μs) than of pyramidal cells (~500μs) or interneurons (~250μs). 2. The voltage change is triphasic. 3. Activity recorded on a tetrode is seen on only one of the four recording wires. In recordings from freely moving rats, axonal signals have been isolated in white matter tracts including the alveus and the corpus callosum as well hippocampal gray matter.[19]
In fact, the generation of action potentials in vivo is sequential in nature, and these sequential spikes constitute the digital codes in the neurons. Although previous studies indicate an axonal origin of a single spike evoked by short-term pulses, physiological signals in vivo trigger the initiation of sequential spikes at the cell bodies of the neurons.[20][21]
In addition to propagating action potentials to axonal terminals, the axon is able to amplify the action potentials, which makes sure a secure propagation of sequential action potentials toward the axonal terminal. In terms of molecular mechanisms, voltage-gated sodium channels in the axons possess lower threshold and shorter refractory period in response to short-term pulses.[22]
Development and growth[edit]
Development[edit]
The development of the axon to its target, is one of the six major stages in the overall development of the nervous system.[23] Studies done on cultured hippocampal neurons suggest that neurons initially produce multiple neurites that are equivalent, yet only one of these neurites is destined to become the axon.[24] It is unclear whether axon specification precedes axon elongation or vice versa,[25] although recent evidence points to the latter. If an axon that is not fully developed is cut, the polarity can change and other neurites can potentially become the axon. This alteration of polarity only occurs when the axon is cut at least 10 μm shorter than the other neurites. After the incision is made, the longest neurite will become the future axon and all the other neurites, including the original axon, will turn into dendrites.[26] Imposing an external force on a neurite, causing it to elongate, will make it become an axon.[27] Nonetheless, axonal development is achieved through a complex interplay between extracellular signaling, intracellular signaling and cytoskeletal dynamics.
[edit]
The extracellular signals that propagate through the extracellular matrix surrounding neurons play a prominent role in axonal development.[28] These signaling molecules include proteins, neurotrophic factors, and extracellular matrix and adhesion molecules.
Netrin (also known as UNC-6) a secreted protein, functions in axon formation. When the UNC-5 netrin receptor is mutated, several neurites are irregularly projected out of neurons and finally a single axon is extended anteriorly.[29][30][31][32] The neurotrophic factors – nerve growth factor (NGF), brain-derived neurotrophic factor (BDNF) and neurotrophin-3 (NTF3) are also involved in axon development and bind to Trk receptors.[33]
The ganglioside-converting enzyme plasma membrane ganglioside sialidase (PMGS), which is involved in the activation of TrkA at the tip of neutrites, is required for the elongation of axons. PMGS asymmetrically distributes to the tip of the neurite that is destined to become the future axon.[34]
Intracellular signaling[edit]
During axonal development, the activity of PI3K is increased at the tip of destined axon. Disrupting the activity of PI3K inhibits axonal development. Activation of PI3K results in the production of phosphatidylinositol (3,4,5)-trisphosphate (PtdIns) which can cause significant elongation of a neurite, converting it into an axon. As such, the overexpression of phosphatases that dephosphorylate PtdIns leads into the failure of polarization.[28]
Cytoskeletal dynamics[edit]
The neurite with the lowest actin filament content will become the axon. PGMS concentration and f-actin content are inversely correlated; when PGMS becomes enriched at the tip of a neurite, its f-actin content is substantially decreased.[34] In addition, exposure to actin-depolimerizing drugs and toxin B (which inactivates Rho-signaling) causes the formation of multiple axons. Consequently, the interruption of the actin network in a growth cone will promote its neurite to become the axon.[35]
Growth[edit]
Axon of nine-day-old mouse with growth cone visible
Growing axons move through their environment via the growth cone, which is at the tip of the axon. The growth cone has a broad sheet-like extension called a lamellipodium which contain protrusions called filopodia. The filopodia are the mechanism by which the entire process adheres to surfaces and explores the surrounding environment. Actin plays a major role in the mobility of this system. Environments with high levels of cell adhesion molecules (CAMs) create an ideal environment for axonal growth. This seems to provide a «sticky» surface for axons to grow along. Examples of CAMs specific to neural systems include N-CAM, TAG-1 – an axonal glycoprotein[36] – and MAG, all of which are part of the immunoglobulin superfamily. Another set of molecules called extracellular matrix-adhesion molecules also provide a sticky substrate for axons to grow along. Examples of these molecules include laminin, fibronectin, tenascin, and perlecan. Some of these are surface bound to cells and thus act as short range attractants or repellents. Others are difusible ligands and thus can have long range effects.
Cells called guidepost cells assist in the guidance of neuronal axon growth. These cells that help axon guidance, are typically other neurons that are sometimes immature. When the axon has completed its growth at its connection to the target, the diameter of the axon can increase by up to five times, depending on the speed of conduction required.[37]
It has also been discovered through research that if the axons of a neuron were damaged, as long as the soma (the cell body of a neuron) is not damaged, the axons would regenerate and remake the synaptic connections with neurons with the help of guidepost cells. This is also referred to as neuroregeneration.[38]
Nogo-A is a type of neurite outgrowth inhibitory component that is present in the central nervous system myelin membranes (found in an axon). It has a crucial role in restricting axonal regeneration in adult mammalian central nervous system. In recent studies, if Nogo-A is blocked and neutralized, it is possible to induce long-distance axonal regeneration which leads to enhancement of functional recovery in rats and mouse spinal cord. This has yet to be done on humans.[39] A recent study has also found that macrophages activated through a specific inflammatory pathway activated by the Dectin-1 receptor are capable of promoting axon recovery, also however causing neurotoxicity in the neuron.[40]
Length regulation[edit]
Axons vary largely in length from a few micrometers up to meters in some animals. This emphasizes that there must be a cellular length regulation mechanism allowing the neurons both to sense the length of their axons and to control their growth accordingly. It was discovered that motor proteins play an important role in regulating the length of axons.[41] Based on this observation, researchers developed an explicit model for axonal growth describing how motor proteins could affect the axon length on the molecular level.[42][43][44][45] These studies suggest that motor proteins carry signaling molecules from the soma to the growth cone and vice versa whose concentration oscillates in time with a length-dependent frequency.
Classification[edit]
The axons of neurons in the human peripheral nervous system can be classified based on their physical features and signal conduction properties. Axons were known to have different thicknesses (from 0.1 to 20 µm)[3] and these differences were thought to relate to the speed at which an action potential could travel along the axon – its conductance velocity. Erlanger and Gasser proved this hypothesis, and identified several types of nerve fiber, establishing a relationship between the diameter of an axon and its nerve conduction velocity. They published their findings in 1941 giving the first classification of axons.
Axons are classified in two systems. The first one introduced by Erlanger and Gasser, grouped the fibers into three main groups using the letters A, B, and C. These groups, group A, group B, and group C include both the sensory fibers (afferents) and the motor fibers (efferents). The first group A, was subdivided into alpha, beta, gamma, and delta fibers – Aα, Aβ, Aγ, and Aδ. The motor neurons of the different motor fibers, were the lower motor neurons – alpha motor neuron, beta motor neuron, and gamma motor neuron having the Aα, Aβ, and Aγ nerve fibers, respectively.
Later findings by other researchers identified two groups of Aa fibers that were sensory fibers. These were then introduced into a system that only included sensory fibers (though some of these were mixed nerves and were also motor fibers). This system refers to the sensory groups as Types and uses Roman numerals: Type Ia, Type Ib, Type II, Type III, and Type IV.
Motor[edit]
Lower motor neurons have two kind of fibers:
Motor fiber types
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin | Conduction velocity (meters/second) |
Associated muscle fibers |
|---|---|---|---|---|---|
| Alpha (α) motor neuron | Aα | 13–20 | Yes | 80–120 | Extrafusal muscle fibers |
| Beta (β) motor neuron | Aβ | ||||
| Gamma (γ) motor neuron | Aγ | 5-8 | Yes | 4–24[46][47] | Intrafusal muscle fibers |
Sensory[edit]
Different sensory receptors innervate different types of nerve fibers. Proprioceptors are innervated by type Ia, Ib and II sensory fibers, mechanoreceptors by type II and III sensory fibers and nociceptors and thermoreceptors by type III and IV sensory fibers.
Sensory fiber types
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin | Conduction velocity (m/s) |
Associated sensory receptors | Proprioceptors | Mechanoceptors | Nociceptors and thermoreceptors |
|---|---|---|---|---|---|---|---|---|
| Ia | Aα | 13–20 | Yes | 80–120 | Primary receptors of muscle spindle (annulospiral ending) | ✔ | ||
| Ib | Aα | 13–20 | Yes | 80–120 | Golgi tendon organ | |||
| II | Aβ | 6–12 | Yes | 33–75 | Secondary receptors of muscle spindle (flower-spray ending). All cutaneous mechanoreceptors |
✔ | ||
| III | Aδ | 1–5 | Thin | 3–30 | Free nerve endings of touch and pressure Nociceptors of lateral spinothalamic tract Cold thermoreceptors |
✔ | ||
| IV | C | 0.2–1.5 | No | 0.5–2.0 | Nociceptors of anterior spinothalamic tract Warmth receptors |
Autonomic[edit]
The autonomic nervous system has two kinds of peripheral fibers:
Fiber types
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin[48] | Conduction velocity (m/s) |
|---|---|---|---|---|
| preganglionic fibers | B | 1–5 | Yes | 3–15 |
| postganglionic fibers | C | 0.2–1.5 | No | 0.5–2.0 |
Clinical significance[edit]
In order of degree of severity, injury to a nerve can be described as neurapraxia, axonotmesis, or neurotmesis.
Concussion is considered a mild form of diffuse axonal injury.[49] Axonal injury can also cause central chromatolysis. The dysfunction of axons in the nervous system is one of the major causes of many inherited neurological disorders that affect both peripheral and central neurons.[5]
When an axon is crushed, an active process of axonal degeneration takes place at the part of the axon furthest from the cell body. This degeneration takes place quickly following the injury, with the part of the axon being sealed off at the membranes and broken down by macrophages. This is known as Wallerian degeneration.[50] Dying back of an axon can also take place in many neurodegenerative diseases, particularly when axonal transport is impaired, this is known as Wallerian-like degeneration.[51] Studies suggest that the degeneration happens as
a result of the axonal protein NMNAT2, being prevented from reaching all of the axon.[52]
Demyelination of axons causes the multitude of neurological symptoms found in the disease multiple sclerosis.
Dysmyelination is the abnormal formation of the myelin sheath. This is implicated in several leukodystrophies, and also in schizophrenia.[53][54][55]
A severe traumatic brain injury can result in widespread lesions to nerve tracts damaging the axons in a condition known as diffuse axonal injury. This can lead to a persistent vegetative state.[56] It has been shown in studies on the rat that axonal damage from a single mild traumatic brain injury, can leave a susceptibility to further damage, after repeated mild traumatic brain injuries.[57]
A nerve guidance conduit is an artificial means of guiding axon growth to enable neuroregeneration, and is one of the many treatments used for different kinds of nerve injury.
History[edit]
German anatomist Otto Friedrich Karl Deiters is generally credited with the discovery of the axon by distinguishing it from the dendrites.[5] Swiss Rüdolf Albert von Kölliker and German Robert Remak were the first to identify and characterize the axon initial segment. Kölliker named the axon in 1896.[58] Louis-Antoine Ranvier was the first to describe the gaps or nodes found on axons and for this contribution these axonal features are now commonly referred to as the nodes of Ranvier. Santiago Ramón y Cajal, a Spanish anatomist, proposed that axons were the output components of neurons, describing their functionality.[5] Joseph Erlanger and Herbert Gasser earlier developed the classification system for peripheral nerve fibers,[59] based on axonal conduction velocity, myelination, fiber size etc. Alan Hodgkin and Andrew Huxley also employed the squid giant axon (1939) and by 1952 they had obtained a full quantitative description of the ionic basis of the action potential, leading to the formulation of the Hodgkin–Huxley model. Hodgkin and Huxley were awarded jointly the Nobel Prize for this work in 1963. The formulae detailing axonal conductance were extended to vertebrates in the Frankenhaeuser–Huxley equations. The understanding of the biochemical basis for action potential propagation has advanced further, and includes many details about individual ion channels.
Other animals[edit]
The axons in invertebrates have been extensively studied. The longfin inshore squid, often used as a model organism has the longest known axon.[60] The giant squid has the largest axon known. Its size ranges from 0.5 (typically) to 1 mm in diameter and is used in the control of its jet propulsion system. The fastest recorded conduction speed of 210 m/s, is found in the ensheathed axons of some pelagic Penaeid shrimps[61] and the usual range is between 90 and 200 meters/s[62] (cf 100–120 m/s for the fastest myelinated vertebrate axon.)
In other cases as seen in rat studies an axon originates from a dendrite; such axons are said to have «dendritic origin». Some axons with dendritic origin similarly have a «proximal» initial segment that starts directly at the axon origin, while others have a «distal» initial segment, discernibly separated from the axon origin.[63] In many species some of the neurons have axons that emanate from the dendrite and not from the cell body, and these are known as axon-carrying dendrites.[1] In many cases, an axon originates at an axon hillock on the soma; such axons are said to have «somatic origin». Some axons with somatic origin have a «proximal» initial segment adjacent the axon hillock, while others have a «distal» initial segment, separated from the soma by an extended axon hillock.[63]
See also[edit]
- Electrophysiology
- Ganglionic eminence
- Giant axonal neuropathy
- Neuronal tracing
- Pioneer axon
References[edit]
- ^ a b Triarhou LC (2014). «Axons emanating from dendrites: phylogenetic repercussions with Cajalian hues». Frontiers in Neuroanatomy. 8: 133. doi:10.3389/fnana.2014.00133. PMC 4235383. PMID 25477788.
- ^ Yau KW (December 1976). «Receptive fields, geometry and conduction block of sensory neurones in the central nervous system of the leech». The Journal of Physiology. 263 (3): 513–38. doi:10.1113/jphysiol.1976.sp011643. PMC 1307715. PMID 1018277.
- ^ a b c Squire, Larry (2013). Fundamental neuroscience (4th ed.). Amsterdam: Elsevier/Academic Press. pp. 61–65. ISBN 978-0-12-385-870-2.
- ^ a b c Luders E, Thompson PM, Toga AW (August 2010). «The development of the corpus callosum in the healthy human brain». The Journal of Neuroscience. 30 (33): 10985–90. doi:10.1523/JNEUROSCI.5122-09.2010. PMC 3197828. PMID 20720105.
- ^ a b c d e Debanne D, Campanac E, Bialowas A, Carlier E, Alcaraz G (April 2011). «Axon physiology» (PDF). Physiological Reviews. 91 (2): 555–602. doi:10.1152/physrev.00048.2009. PMID 21527732. S2CID 13916255.
- ^ Nelson AD, Jenkins PM (2017). «Axonal Membranes and Their Domains: Assembly and Function of the Axon Initial Segment and Node of Ranvier». Frontiers in Cellular Neuroscience. 11: 136. doi:10.3389/fncel.2017.00136. PMC 5422562. PMID 28536506.
- ^ Leterrier C, Clerc N, Rueda-Boroni F, Montersino A, Dargent B, Castets F (2017). «Ankyrin G Membrane Partners Drive the Establishment and Maintenance of the Axon Initial Segment». Frontiers in Cellular Neuroscience. 11: 6. doi:10.3389/fncel.2017.00006. PMC 5266712. PMID 28184187.
- ^ Leterrier C (February 2018). «The Axon Initial Segment: An Updated Viewpoint». The Journal of Neuroscience. 38 (9): 2135–2145. doi:10.1523/jneurosci.1922-17.2018. PMC 6596274. PMID 29378864.
- ^ Rasband MN (August 2010). «The axon initial segment and the maintenance of neuronal polarity». Nature Reviews. Neuroscience. 11 (8): 552–62. doi:10.1038/nrn2852. PMID 20631711. S2CID 23996233.
- ^ a b c d Jones SL, Svitkina TM (2016). «Axon Initial Segment Cytoskeleton: Architecture, Development, and Role in Neuron Polarity». Neural Plasticity. 2016: 6808293. doi:10.1155/2016/6808293. PMC 4967436. PMID 27493806.
- ^ Clark BD, Goldberg EM, Rudy B (December 2009). «Electrogenic tuning of the axon initial segment». The Neuroscientist. 15 (6): 651–68. doi:10.1177/1073858409341973. PMC 2951114. PMID 20007821.
- ^ a b Yamada R, Kuba H (2016). «Structural and Functional Plasticity at the Axon Initial Segment». Frontiers in Cellular Neuroscience. 10: 250. doi:10.3389/fncel.2016.00250. PMC 5078684. PMID 27826229.
- ^ a b Susuki K, Kuba H (March 2016). «Activity-dependent regulation of excitable axonal domains». The Journal of Physiological Sciences. 66 (2): 99–104. doi:10.1007/s12576-015-0413-4. PMID 26464228. S2CID 18862030.
- ^ a b c d e Alberts B (2004). Essential cell biology: an introduction to the molecular biology of the cell (2nd ed.). New York: Garland. pp. 584–587. ISBN 978-0-8153-3481-1.
- ^ a b Alberts B (2002). Molecular biology of the cell (4th ed.). New York: Garland. pp. 979–981. ISBN 978-0-8153-4072-0.
- ^ Ozgen, H; Baron, W; Hoekstra, D; Kahya, N (September 2016). «Oligodendroglial membrane dynamics in relation to myelin biogenesis». Cellular and Molecular Life Sciences. 73 (17): 3291–310. doi:10.1007/s00018-016-2228-8. PMC 4967101. PMID 27141942.
- ^ Sadler, T. (2010). Langman’s medical embryology (11th ed.). Philadelphia: Lippincott William & Wilkins. p. 300. ISBN 978-0-7817-9069-7.
- ^ Hess A, Young JZ (November 1952). «The nodes of Ranvier». Proceedings of the Royal Society of London. Series B, Biological Sciences. Series B. 140 (900): 301–20. Bibcode:1952RSPSB.140..301H. doi:10.1098/rspb.1952.0063. JSTOR 82721. PMID 13003931. S2CID 11963512.
- ^ Robbins AA, Fox SE, Holmes GL, Scott RC, Barry JM (November 2013). «Short duration waveforms recorded extracellularly from freely moving rats are representative of axonal activity». Frontiers in Neural Circuits. 7 (181): 181. doi:10.3389/fncir.2013.00181. PMC 3831546. PMID 24348338.
- ^ Rongjing Ge, Hao Qian and Jin-Hui Wang* (2011) Molecular Brain 4(19), 1~11
- ^ Rongjing Ge, Hao Qian, Na Chen and Jin-Hui Wang* (2014) Molecular Brain 7(26):1-16
- ^ Chen N, Yu J, Qian H, Ge R, Wang JH (July 2010). «Axons amplify somatic incomplete spikes into uniform amplitudes in mouse cortical pyramidal neurons». PLOS ONE. 5 (7): e11868. Bibcode:2010PLoSO…511868C. doi:10.1371/journal.pone.0011868. PMC 2912328. PMID 20686619.
- ^ Wolpert, Lewis (2015). Principles of development (5th ed.). pp. 520–524. ISBN 978-0-19-967814-3.
- ^ Fletcher TL, Banker GA (December 1989). «The establishment of polarity by hippocampal neurons: the relationship between the stage of a cell’s development in situ and its subsequent development in culture». Developmental Biology. 136 (2): 446–54. doi:10.1016/0012-1606(89)90269-8. PMID 2583372.
- ^ Jiang H, Rao Y (May 2005). «Axon formation: fate versus growth». Nature Neuroscience. 8 (5): 544–6. doi:10.1038/nn0505-544. PMID 15856056. S2CID 27728967.
- ^ Goslin K, Banker G (April 1989). «Experimental observations on the development of polarity by hippocampal neurons in culture». The Journal of Cell Biology. 108 (4): 1507–16. doi:10.1083/jcb.108.4.1507. PMC 2115496. PMID 2925793.
- ^ Lamoureux P, Ruthel G, Buxbaum RE, Heidemann SR (November 2002). «Mechanical tension can specify axonal fate in hippocampal neurons». The Journal of Cell Biology. 159 (3): 499–508. doi:10.1083/jcb.200207174. PMC 2173080. PMID 12417580.
- ^ a b Arimura N, Kaibuchi K (March 2007). «Neuronal polarity: from extracellular signals to intracellular mechanisms». Nature Reviews. Neuroscience. 8 (3): 194–205. doi:10.1038/nrn2056. PMID 17311006. S2CID 15556921.
- ^ Neuroglia and pioneer neurons express UNC-6 to provide global and local netrin cues for guiding migrations in C. elegans
- ^ Serafini T, Kennedy TE, Galko MJ, Mirzayan C, Jessell TM, Tessier-Lavigne M (August 1994). «The netrins define a family of axon outgrowth-promoting proteins homologous to C. elegans UNC-6». Cell. 78 (3): 409–24. doi:10.1016/0092-8674(94)90420-0. PMID 8062384. S2CID 22666205.
- ^ Hong K, Hinck L, Nishiyama M, Poo MM, Tessier-Lavigne M, Stein E (June 1999). «A ligand-gated association between cytoplasmic domains of UNC5 and DCC family receptors converts netrin-induced growth cone attraction to repulsion». Cell. 97 (7): 927–41. doi:10.1016/S0092-8674(00)80804-1. PMID 10399920. S2CID 18043414.
- ^ Hedgecock EM, Culotti JG, Hall DH (January 1990). «The unc-5, unc-6, and unc-40 genes guide circumferential migrations of pioneer axons and mesodermal cells on the epidermis in C. elegans». Neuron. 4 (1): 61–85. doi:10.1016/0896-6273(90)90444-K. PMID 2310575. S2CID 23974242.
- ^ Huang EJ, Reichardt LF (2003). «Trk receptors: roles in neuronal signal transduction». Annual Review of Biochemistry. 72: 609–42. doi:10.1146/annurev.biochem.72.121801.161629. PMID 12676795. S2CID 10217268.
- ^ a b Da Silva JS, Hasegawa T, Miyagi T, Dotti CG, Abad-Rodriguez J (May 2005). «Asymmetric membrane ganglioside sialidase activity specifies axonal fate». Nature Neuroscience. 8 (5): 606–15. doi:10.1038/nn1442. PMID 15834419. S2CID 25227765.
- ^ Bradke F, Dotti CG (March 1999). «The role of local actin instability in axon formation». Science. 283 (5409): 1931–4. Bibcode:1999Sci…283.1931B. doi:10.1126/science.283.5409.1931. PMID 10082468.
- ^ Furley AJ, Morton SB, Manalo D, Karagogeos D, Dodd J, Jessell TM (April 1990). «The axonal glycoprotein TAG-1 is an immunoglobulin superfamily member with neurite outgrowth-promoting activity». Cell. 61 (1): 157–70. doi:10.1016/0092-8674(90)90223-2. PMID 2317872. S2CID 28813676.
- ^ Alberts, Bruce (2015). Molecular biology of the cell (Sixth ed.). p. 947. ISBN 9780815344643.
- ^ Kunik D, Dion C, Ozaki T, Levin LA, Costantino S (2011). «Laser-based single-axon transection for high-content axon injury and regeneration studies». PLOS ONE. 6 (11): e26832. Bibcode:2011PLoSO…626832K. doi:10.1371/journal.pone.0026832. PMC 3206876. PMID 22073205.
- ^ Schwab ME (February 2004). «Nogo and axon regeneration». Current Opinion in Neurobiology. 14 (1): 118–24. doi:10.1016/j.conb.2004.01.004. PMID 15018947. S2CID 9672315.
- ^ Gensel JC, Nakamura S, Guan Z, van Rooijen N, Ankeny DP, Popovich PG (March 2009). «Macrophages promote axon regeneration with concurrent neurotoxicity». The Journal of Neuroscience. 29 (12): 3956–68. doi:10.1523/JNEUROSCI.3992-08.2009. PMC 2693768. PMID 19321792.
- ^ Myers KA, Baas PW (September 2007). «Kinesin-5 regulates the growth of the axon by acting as a brake on its microtubule array». The Journal of Cell Biology. 178 (6): 1081–91. doi:10.1083/jcb.200702074. PMC 2064629. PMID 17846176.
- ^ Rishal I, Kam N, Perry RB, Shinder V, Fisher EM, Schiavo G, Fainzilber M (June 2012). «A motor-driven mechanism for cell-length sensing». Cell Reports. 1 (6): 608–16. doi:10.1016/j.celrep.2012.05.013. PMC 3389498. PMID 22773964.
- ^ Karamched BR, Bressloff PC (May 2015). «Delayed feedback model of axonal length sensing». Biophysical Journal. 108 (9): 2408–19. Bibcode:2015BpJ…108.2408K. doi:10.1016/j.bpj.2015.03.055. PMC 4423051. PMID 25954897.
- ^ Bressloff PC, Karamched BR (2015). «A frequency-dependent decoding mechanism for axonal length sensing». Frontiers in Cellular Neuroscience. 9: 281. doi:10.3389/fncel.2015.00281. PMC 4508512. PMID 26257607.
- ^ Folz F, Wettmann L, Morigi G, Kruse K (May 2019). «Sound of an axon’s growth». Physical Review E. 99 (5–1): 050401. arXiv:1807.04799. Bibcode:2019PhRvE..99e0401F. doi:10.1103/PhysRevE.99.050401. PMID 31212501. S2CID 118682719.
- ^ Andrew BL, Part NJ (April 1972). «Properties of fast and slow motor units in hind limb and tail muscles of the rat». Quarterly Journal of Experimental Physiology and Cognate Medical Sciences. 57 (2): 213–25. doi:10.1113/expphysiol.1972.sp002151. PMID 4482075.
- ^ Russell NJ (January 1980). «Axonal conduction velocity changes following muscle tenotomy or deafferentation during development in the rat». The Journal of Physiology. 298: 347–60. doi:10.1113/jphysiol.1980.sp013085. PMC 1279120. PMID 7359413.
- ^ Pocock G, Richards CD, et al. (2004). Human Physiology (2nd ed.). New York: Oxford University Press. pp. 187–189. ISBN 978-0-19-858527-5.
- ^ Dawodu ST (16 August 2017). «Traumatic Brain Injury (TBI) — Definition, Epidemiology, Pathophysiology». Medscape. Archived from the original on 12 June 2018. Retrieved 14 July 2018.
- ^ Trauma and Wallerian Degeneration Archived 2 May 2006 at the Wayback Machine, University of California, San Francisco
- ^ Coleman MP, Freeman MR (1 June 2010). «Wallerian degeneration, wld(s), and nmnat». Annual Review of Neuroscience. 33 (1): 245–67. doi:10.1146/annurev-neuro-060909-153248. PMC 5223592. PMID 20345246.
- ^ Gilley J, Coleman MP (January 2010). «Endogenous Nmnat2 is an essential survival factor for maintenance of healthy axons». PLOS Biology. 8 (1): e1000300. doi:10.1371/journal.pbio.1000300. PMC 2811159. PMID 20126265.
- ^ Krämer-Albers EM, Gehrig-Burger K, Thiele C, Trotter J, Nave KA (November 2006). «Perturbed interactions of mutant proteolipid protein/DM20 with cholesterol and lipid rafts in oligodendroglia: implications for dysmyelination in spastic paraplegia». The Journal of Neuroscience. 26 (45): 11743–52. doi:10.1523/JNEUROSCI.3581-06.2006. PMC 6674790. PMID 17093095.
- ^ Matalon R, Michals-Matalon K, Surendran S, Tyring SK (2006). «Canavan disease: studies on the knockout mouse». N-Acetylaspartate. Adv. Exp. Med. Biol. Advances in Experimental Medicine and Biology. Vol. 576. pp. 77–93, discussion 361–3. doi:10.1007/0-387-30172-0_6. ISBN 978-0-387-30171-6. PMID 16802706. S2CID 44405442.
- ^ Tkachev D, Mimmack ML, Huffaker SJ, Ryan M, Bahn S (August 2007). «Further evidence for altered myelin biosynthesis and glutamatergic dysfunction in schizophrenia». The International Journal of Neuropsychopharmacology. 10 (4): 557–63. doi:10.1017/S1461145706007334. PMID 17291371.
- ^ «Brain Injury, Traumatic». Medcyclopaedia. GE. Archived from the original on 26 May 2011. Retrieved 20 June 2018.
- ^ Wright DK, Brady RD, Kamnaksh A, Trezise J, Sun M, McDonald SJ, et al. (October 2019). «Repeated mild traumatic brain injuries induce persistent changes in plasma protein and magnetic resonance imaging biomarkers in the rat». Scientific Reports. 9 (1): 14626. Bibcode:2019NatSR…914626W. doi:10.1038/s41598-019-51267-w. PMC 6787341. PMID 31602002.
- ^ Finger S (1994). Origins of neuroscience: a history of explorations into brain function. Oxford University Press. p. 47. ISBN 9780195146943. OCLC 27151391.
Kölliker would give the «axon» its name in 1896.
- ^ Grant G (December 2006). «The 1932 and 1944 Nobel Prizes in physiology or medicine: rewards for ground-breaking studies in neurophysiology». Journal of the History of the Neurosciences. 15 (4): 341–57. doi:10.1080/09647040600638981. PMID 16997762. S2CID 37676544.
- ^ Hellier, Jennifer L. (16 December 2014). The Brain, the Nervous System, and Their Diseases [3 volumes]. ABC-CLIO. ISBN 9781610693387. Archived from the original on 14 March 2018.
- ^ Hsu K, Terakawa S (July 1996). «Fenestration in the myelin sheath of nerve fibers of the shrimp: a novel node of excitation for saltatory conduction». Journal of Neurobiology. 30 (3): 397–409. doi:10.1002/(SICI)1097-4695(199607)30:3<397::AID-NEU8>3.0.CO;2-#. PMID 8807532.
- ^ Salzer JL, Zalc B (October 2016). «Myelination». Current Biology. 26 (20): R971–R975. doi:10.1016/j.cub.2016.07.074. PMID 27780071.
- ^ a b Höfflin F, Jack A, Riedel C, Mack-Bucher J, Roos J, Corcelli C, et al. (2017). «Heterogeneity of the Axon Initial Segment in Interneurons and Pyramidal Cells of Rodent Visual Cortex». Frontiers in Cellular Neuroscience. 11: 332. doi:10.3389/fncel.2017.00332. PMC 5684645. PMID 29170630.
External links[edit]
- Histology image: 3_09 at the University of Oklahoma Health Sciences Center – «Slide 3 Spinal cord»
Элементы нейронных сетей
Искусственный нейрон (формальный нейрон) — элемент искусственных нейронных сетей, моделирующий некоторые функции биологического нейрона.
Главная функция искусственного нейрона — формировать выходной сигнал в зависимости от сигналов, поступающих на его входы.
В самой распространенной конфигурации входные сигналы обрабатываются адаптивным сумматором, затем выходной сигнал сумматора поступает в нелинейный преобразователь, где преобразуется функцией активации, и результат подается на выход (в точку ветвления ).
Общий вид искусственного нейрона приведен на рис. 11.1.
Рис.
11.1.
Искусственный нейрон
Нейрон характеризуется текущим состоянием и обладает группой синапсов — однонаправленных входных связей, соединенных с выходами других нейронов.
Нейрон имеет аксон — выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов.
Каждый синапс характеризуется величиной синаптической связи (ее весом wi).
Текущее состояние нейрона определяется как взвешенная сумма его входов:
Выход нейрона есть функция его состояния:
Активационная функция, которую также называют характеристической функцией, — это нелинейная функция, вычисляющая выходной сигнал формального нейрона.
Часто используемые активационные функции:
- Жесткая пороговая функция.
- Линейный порог.
- Сигмоидальная функция.
Выбор активационной функции определяется спецификой поставленной задачи либо ограничениями, накладываемыми некоторыми алгоритмами обучения.
Нелинейный преобразователь — это элемент искусственного нейрона, преобразующий текущее состояние нейрона (выходной сигнал адаптивного сумматора) в выходной сигнал нейрона по некоторому нелинейному закону ( активационной функции ).
Точка ветвления (выход) — это элемент формального нейрона, посылающий его выходной сигнал по нескольким адресам и имеющий один вход и несколько выходов.
На вход точки ветвления обычно подается выходной сигнал нелинейного преобразователя, который затем посылается на входы других нейронов.
| Axon | |
|---|---|

An axon of a multipolar neuron |
|
| Identifiers | |
| MeSH | D001369 |
| FMA | 67308 |
| Anatomical terminology
[edit on Wikidata] |
An axon (from Greek ἄξων áxōn, axis), or nerve fiber (or nerve fibre: see spelling differences), is a long, slender projection of a nerve cell, or neuron, in vertebrates, that typically conducts electrical impulses known as action potentials away from the nerve cell body. The function of the axon is to transmit information to different neurons, muscles, and glands. In certain sensory neurons (pseudounipolar neurons), such as those for touch and warmth, the axons are called afferent nerve fibers and the electrical impulse travels along these from the periphery to the cell body and from the cell body to the spinal cord along another branch of the same axon. Axon dysfunction can be the cause of many inherited and acquired neurological disorders that affect both the peripheral and central neurons. Nerve fibers are classed into three types – group A nerve fibers, group B nerve fibers, and group C nerve fibers. Groups A and B are myelinated, and group C are unmyelinated. These groups include both sensory fibers and motor fibers. Another classification groups only the sensory fibers as Type I, Type II, Type III, and Type IV.
An axon is one of two types of cytoplasmic protrusions from the cell body of a neuron; the other type is a dendrite. Axons are distinguished from dendrites by several features, including shape (dendrites often taper while axons usually maintain a constant radius), length (dendrites are restricted to a small region around the cell body while axons can be much longer), and function (dendrites receive signals whereas axons transmit them). Some types of neurons have no axon and transmit signals from their dendrites. In some species, axons can emanate from dendrites known as axon-carrying dendrites.[1] No neuron ever has more than one axon; however in invertebrates such as insects or leeches the axon sometimes consists of several regions that function more or less independently of each other.[2]
Axons are covered by a membrane known as an axolemma; the cytoplasm of an axon is called axoplasm. Most axons branch, in some cases very profusely. The end branches of an axon are called telodendria. The swollen end of a telodendron is known as the axon terminal which joins the dendron or cell body of another neuron forming a synaptic connection. Axons make contact with other cells – usually other neurons but sometimes muscle or gland cells – at junctions called synapses. In some circumstances, the axon of one neuron may form a synapse with the dendrites of the same neuron, resulting in an autapse. At a synapse, the membrane of the axon closely adjoins the membrane of the target cell, and special molecular structures serve to transmit electrical or electrochemical signals across the gap. Some synaptic junctions appear along the length of an axon as it extends; these are called en passant («in passing») synapses and can be in the hundreds or even the thousands along one axon.[3] Other synapses appear as terminals at the ends of axonal branches.
A single axon, with all its branches taken together, can innervate multiple parts of the brain and generate thousands of synaptic terminals. A bundle of axons make a nerve tract in the central nervous system,[4] and a fascicle in the peripheral nervous system. In placental mammals the largest white matter tract in the brain is the corpus callosum, formed of some 200 million axons in the human brain.[4]
Anatomy[edit]
A typical myelinated axon
Axons are the primary transmission lines of the nervous system, and as bundles they form nerves. Some axons can extend up to one meter or more while others extend as little as one millimeter. The longest axons in the human body are those of the sciatic nerve, which run from the base of the spinal cord to the big toe of each foot. The diameter of axons is also variable. Most individual axons are microscopic in diameter (typically about one micrometer (µm) across). The largest mammalian axons can reach a diameter of up to 20 µm. The squid giant axon, which is specialized to conduct signals very rapidly, is close to 1 millimeter in diameter, the size of a small pencil lead. The numbers of axonal telodendria (the branching structures at the end of the axon) can also differ from one nerve fiber to the next. Axons in the central nervous system (CNS) typically show multiple telodendria, with many synaptic end points. In comparison, the cerebellar granule cell axon is characterized by a single T-shaped branch node from which two parallel fibers extend. Elaborate branching allows for the simultaneous transmission of messages to a large number of target neurons within a single region of the brain.
There are two types of axons in the nervous system: myelinated and unmyelinated axons.[5] Myelin is a layer of a fatty insulating substance, which is formed by two types of glial cells: Schwann cells and oligodendrocytes. In the peripheral nervous system Schwann cells form the myelin sheath of a myelinated axon. Oligodendrocytes form the insulating myelin in the CNS. Along myelinated nerve fibers, gaps in the myelin sheath known as nodes of Ranvier occur at evenly spaced intervals. The myelination enables an especially rapid mode of electrical impulse propagation called saltatory conduction.
The myelinated axons from the cortical neurons form the bulk of the neural tissue called white matter in the brain. The myelin gives the white appearance to the tissue in contrast to the grey matter of the cerebral cortex which contains the neuronal cell bodies. A similar arrangement is seen in the cerebellum. Bundles of myelinated axons make up the nerve tracts in the CNS. Where these tracts cross the midline of the brain to connect opposite regions they are called commissures. The largest of these is the corpus callosum that connects the two cerebral hemispheres, and this has around 20 million axons.[4]
The structure of a neuron is seen to consist of two separate functional regions, or compartments – the cell body together with the dendrites as one region, and the axonal region as the other.
Axonal region[edit]
The axonal region or compartment, includes the axon hillock, the initial segment, the rest of the axon, and the axon telodendria, and axon terminals. It also includes the myelin sheath. The Nissl bodies that produce the neuronal proteins are absent in the axonal region.[3] Proteins needed for the growth of the axon, and the removal of waste materials, need a framework for transport. This axonal transport is provided for in the axoplasm by arrangements of microtubules and intermediate filaments known as neurofilaments.
Axon hillock[edit]
Detail showing microtubules at axon hillock and initial segment.
The axon hillock is the area formed from the cell body of the neuron as it extends to become the axon. It precedes the initial segment. The received action potentials that are summed in the neuron are transmitted to the axon hillock for the generation of an action potential from the initial segment.
Axonal initial segment[edit]
The axonal initial segment (AIS) is a structurally and functionally separate microdomain of the axon.[6][7] One function of the initial segment is to separate the main part of an axon from the rest of the neuron; another function is to help initiate action potentials.[8] Both of these functions support neuron cell polarity, in which dendrites (and, in some cases the soma) of a neuron receive input signals at the basal region, and at the apical region the neuron’s axon provides output signals.[9]
The axon initial segment is unmyelinated and contains a specialized complex of proteins. It is between approximately 20 and 60 µm in length and functions as the site of action potential initiation.[10][11] Both the position on the axon and the length of the AIS can change showing a degree of plasticity that can fine-tune the neuronal output.[10][12] A longer AIS is associated with a greater excitability.[12] Plasticity is also seen in the ability of the AIS to change its distribution and to maintain the activity of neural circuitry at a constant level.[13]
The AIS is highly specialized for the fast conduction of nerve impulses. This is achieved by a high concentration of voltage-gated sodium channels in the initial segment where the action potential is initiated.[13] The ion channels are accompanied by a high number of cell adhesion molecules and scaffolding proteins that anchor them to the cytoskeleton.[10] Interactions with ankyrin G are important as it is the major organizer in the AIS.[10]
Axonal transport[edit]
The axoplasm is the equivalent of cytoplasm in the cell. Microtubules form in the axoplasm at the axon hillock. They are arranged along the length of the axon, in overlapping sections, and all point in the same direction – towards the axon terminals.[14] This is noted by the positive endings of the microtubules. This overlapping arrangement provides the routes for the transport of different materials from the cell body.[14] Studies on the axoplasm has shown the movement of numerous vesicles of all sizes to be seen along cytoskeletal filaments – the microtubules, and neurofilaments, in both directions between the axon and its terminals and the cell body.
Outgoing anterograde transport from the cell body along the axon, carries mitochondria and membrane proteins needed for growth to the axon terminal. Ingoing retrograde transport carries cell waste materials from the axon terminal to the cell body.[15] Outgoing and ingoing tracks use different sets of motor proteins.[14] Outgoing transport is provided by kinesin, and ingoing return traffic is provided by dynein. Dynein is minus-end directed.[15] There are many forms of kinesin and dynein motor proteins, and each is thought to carry a different cargo.[14] The studies on transport in the axon led to the naming of kinesin.[14]
Myelination[edit]
TEM of a myelinated axon in cross-section.
In the nervous system, axons may be myelinated, or unmyelinated. This is the provision of an insulating layer, called a myelin sheath. The myelin membrane is unique in its relatively high lipid to protein ratio.[16]
In the peripheral nervous system axons are myelinated by glial cells known as Schwann cells. In the central nervous system the myelin sheath is provided by another type of glial cell, the oligodendrocyte. Schwann cells myelinate a single axon. An oligodendrocyte can myelinate up to 50 axons.[17]
The composition of myelin is different in the two types. In the CNS the major myelin protein is proteolipid protein, and in the PNS it is myelin basic protein.
Nodes of Ranvier[edit]
Nodes of Ranvier (also known as myelin sheath gaps) are short unmyelinated segments of a myelinated axon, which are found periodically interspersed between segments of the myelin sheath. Therefore, at the point of the node of Ranvier, the axon is reduced in diameter.[18] These nodes are areas where action potentials can be generated. In saltatory conduction, electrical currents produced at each node of Ranvier are conducted with little attenuation to the next node in line, where they remain strong enough to generate another action potential. Thus in a myelinated axon, action potentials effectively «jump» from node to node, bypassing the myelinated stretches in between, resulting in a propagation speed much faster than even the fastest unmyelinated axon can sustain.
Axon terminals[edit]
An axon can divide into many branches called telodendria (Greek for ‘end of tree’). At the end of each telodendron is an axon terminal (also called a synaptic bouton, or terminal bouton). Axon terminals contain synaptic vesicles that store the neurotransmitter for release at the synapse. This makes multiple synaptic connections with other neurons possible. Sometimes the axon of a neuron may synapse onto dendrites of the same neuron, when it is known as an autapse.
Action potentials[edit]
| Structure of a typical chemical synapse |
|---|
|
Postsynaptic Voltage- Synaptic Neurotransmitter Receptor Neurotransmitter Axon terminal Synaptic cleft Dendrite |
Most axons carry signals in the form of action potentials, which are discrete electrochemical impulses that travel rapidly along an axon, starting at the cell body and terminating at points where the axon makes synaptic contact with target cells. The defining characteristic of an action potential is that it is «all-or-nothing» – every action potential that an axon generates has essentially the same size and shape. This all-or-nothing characteristic allows action potentials to be transmitted from one end of a long axon to the other without any reduction in size. There are, however, some types of neurons with short axons that carry graded electrochemical signals, of variable amplitude.
When an action potential reaches a presynaptic terminal, it activates the synaptic transmission process. The first step is rapid opening of calcium ion channels in the membrane of the axon, allowing calcium ions to flow inward across the membrane. The resulting increase in intracellular calcium concentration causes synaptic vesicles (tiny containers enclosed by a lipid membrane) filled with a neurotransmitter chemical to fuse with the axon’s membrane and empty their contents into the extracellular space. The neurotransmitter is released from the presynaptic nerve through exocytosis. The neurotransmitter chemical then diffuses across to receptors located on the membrane of the target cell. The neurotransmitter binds to these receptors and activates them. Depending on the type of receptors that are activated, the effect on the target cell can be to excite the target cell, inhibit it, or alter its metabolism in some way. This entire sequence of events often takes place in less than a thousandth of a second. Afterward, inside the presynaptic terminal, a new set of vesicles is moved into position next to the membrane, ready to be released when the next action potential arrives. The action potential is the final electrical step in the integration of synaptic messages at the scale of the neuron.[5]
(A) pyramidal cell, interneuron, and short durationwaveform (Axon), overlay of the three average waveforms;
(B) Average and standard error of peak-trough time for pyramidal cells interneurons, and putative axons;
(C) Scatter plot of signal to noise ratios for individual units againstpeak-trough time for axons, pyramidal cells (PYR) and interneurons (INT).
Extracellular recordings of action potential propagation in axons has been demonstrated in freely moving animals. While extracellular somatic action potentials have been used to study cellular activity in freely moving animals such as place cells, axonal activity in both white and gray matter can also be recorded. Extracellular recordings of axon action potential propagation is distinct from somatic action potentials in three ways: 1. The signal has a shorter peak-trough duration (~150μs) than of pyramidal cells (~500μs) or interneurons (~250μs). 2. The voltage change is triphasic. 3. Activity recorded on a tetrode is seen on only one of the four recording wires. In recordings from freely moving rats, axonal signals have been isolated in white matter tracts including the alveus and the corpus callosum as well hippocampal gray matter.[19]
In fact, the generation of action potentials in vivo is sequential in nature, and these sequential spikes constitute the digital codes in the neurons. Although previous studies indicate an axonal origin of a single spike evoked by short-term pulses, physiological signals in vivo trigger the initiation of sequential spikes at the cell bodies of the neurons.[20][21]
In addition to propagating action potentials to axonal terminals, the axon is able to amplify the action potentials, which makes sure a secure propagation of sequential action potentials toward the axonal terminal. In terms of molecular mechanisms, voltage-gated sodium channels in the axons possess lower threshold and shorter refractory period in response to short-term pulses.[22]
Development and growth[edit]
Development[edit]
The development of the axon to its target, is one of the six major stages in the overall development of the nervous system.[23] Studies done on cultured hippocampal neurons suggest that neurons initially produce multiple neurites that are equivalent, yet only one of these neurites is destined to become the axon.[24] It is unclear whether axon specification precedes axon elongation or vice versa,[25] although recent evidence points to the latter. If an axon that is not fully developed is cut, the polarity can change and other neurites can potentially become the axon. This alteration of polarity only occurs when the axon is cut at least 10 μm shorter than the other neurites. After the incision is made, the longest neurite will become the future axon and all the other neurites, including the original axon, will turn into dendrites.[26] Imposing an external force on a neurite, causing it to elongate, will make it become an axon.[27] Nonetheless, axonal development is achieved through a complex interplay between extracellular signaling, intracellular signaling and cytoskeletal dynamics.
[edit]
The extracellular signals that propagate through the extracellular matrix surrounding neurons play a prominent role in axonal development.[28] These signaling molecules include proteins, neurotrophic factors, and extracellular matrix and adhesion molecules.
Netrin (also known as UNC-6) a secreted protein, functions in axon formation. When the UNC-5 netrin receptor is mutated, several neurites are irregularly projected out of neurons and finally a single axon is extended anteriorly.[29][30][31][32] The neurotrophic factors – nerve growth factor (NGF), brain-derived neurotrophic factor (BDNF) and neurotrophin-3 (NTF3) are also involved in axon development and bind to Trk receptors.[33]
The ganglioside-converting enzyme plasma membrane ganglioside sialidase (PMGS), which is involved in the activation of TrkA at the tip of neutrites, is required for the elongation of axons. PMGS asymmetrically distributes to the tip of the neurite that is destined to become the future axon.[34]
Intracellular signaling[edit]
During axonal development, the activity of PI3K is increased at the tip of destined axon. Disrupting the activity of PI3K inhibits axonal development. Activation of PI3K results in the production of phosphatidylinositol (3,4,5)-trisphosphate (PtdIns) which can cause significant elongation of a neurite, converting it into an axon. As such, the overexpression of phosphatases that dephosphorylate PtdIns leads into the failure of polarization.[28]
Cytoskeletal dynamics[edit]
The neurite with the lowest actin filament content will become the axon. PGMS concentration and f-actin content are inversely correlated; when PGMS becomes enriched at the tip of a neurite, its f-actin content is substantially decreased.[34] In addition, exposure to actin-depolimerizing drugs and toxin B (which inactivates Rho-signaling) causes the formation of multiple axons. Consequently, the interruption of the actin network in a growth cone will promote its neurite to become the axon.[35]
Growth[edit]
Axon of nine-day-old mouse with growth cone visible
Growing axons move through their environment via the growth cone, which is at the tip of the axon. The growth cone has a broad sheet-like extension called a lamellipodium which contain protrusions called filopodia. The filopodia are the mechanism by which the entire process adheres to surfaces and explores the surrounding environment. Actin plays a major role in the mobility of this system. Environments with high levels of cell adhesion molecules (CAMs) create an ideal environment for axonal growth. This seems to provide a «sticky» surface for axons to grow along. Examples of CAMs specific to neural systems include N-CAM, TAG-1 – an axonal glycoprotein[36] – and MAG, all of which are part of the immunoglobulin superfamily. Another set of molecules called extracellular matrix-adhesion molecules also provide a sticky substrate for axons to grow along. Examples of these molecules include laminin, fibronectin, tenascin, and perlecan. Some of these are surface bound to cells and thus act as short range attractants or repellents. Others are difusible ligands and thus can have long range effects.
Cells called guidepost cells assist in the guidance of neuronal axon growth. These cells that help axon guidance, are typically other neurons that are sometimes immature. When the axon has completed its growth at its connection to the target, the diameter of the axon can increase by up to five times, depending on the speed of conduction required.[37]
It has also been discovered through research that if the axons of a neuron were damaged, as long as the soma (the cell body of a neuron) is not damaged, the axons would regenerate and remake the synaptic connections with neurons with the help of guidepost cells. This is also referred to as neuroregeneration.[38]
Nogo-A is a type of neurite outgrowth inhibitory component that is present in the central nervous system myelin membranes (found in an axon). It has a crucial role in restricting axonal regeneration in adult mammalian central nervous system. In recent studies, if Nogo-A is blocked and neutralized, it is possible to induce long-distance axonal regeneration which leads to enhancement of functional recovery in rats and mouse spinal cord. This has yet to be done on humans.[39] A recent study has also found that macrophages activated through a specific inflammatory pathway activated by the Dectin-1 receptor are capable of promoting axon recovery, also however causing neurotoxicity in the neuron.[40]
Length regulation[edit]
Axons vary largely in length from a few micrometers up to meters in some animals. This emphasizes that there must be a cellular length regulation mechanism allowing the neurons both to sense the length of their axons and to control their growth accordingly. It was discovered that motor proteins play an important role in regulating the length of axons.[41] Based on this observation, researchers developed an explicit model for axonal growth describing how motor proteins could affect the axon length on the molecular level.[42][43][44][45] These studies suggest that motor proteins carry signaling molecules from the soma to the growth cone and vice versa whose concentration oscillates in time with a length-dependent frequency.
Classification[edit]
The axons of neurons in the human peripheral nervous system can be classified based on their physical features and signal conduction properties. Axons were known to have different thicknesses (from 0.1 to 20 µm)[3] and these differences were thought to relate to the speed at which an action potential could travel along the axon – its conductance velocity. Erlanger and Gasser proved this hypothesis, and identified several types of nerve fiber, establishing a relationship between the diameter of an axon and its nerve conduction velocity. They published their findings in 1941 giving the first classification of axons.
Axons are classified in two systems. The first one introduced by Erlanger and Gasser, grouped the fibers into three main groups using the letters A, B, and C. These groups, group A, group B, and group C include both the sensory fibers (afferents) and the motor fibers (efferents). The first group A, was subdivided into alpha, beta, gamma, and delta fibers – Aα, Aβ, Aγ, and Aδ. The motor neurons of the different motor fibers, were the lower motor neurons – alpha motor neuron, beta motor neuron, and gamma motor neuron having the Aα, Aβ, and Aγ nerve fibers, respectively.
Later findings by other researchers identified two groups of Aa fibers that were sensory fibers. These were then introduced into a system that only included sensory fibers (though some of these were mixed nerves and were also motor fibers). This system refers to the sensory groups as Types and uses Roman numerals: Type Ia, Type Ib, Type II, Type III, and Type IV.
Motor[edit]
Lower motor neurons have two kind of fibers:
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin | Conduction velocity (meters/second) |
Associated muscle fibers |
|---|---|---|---|---|---|
| Alpha (α) motor neuron | Aα | 13–20 | Yes | 80–120 | Extrafusal muscle fibers |
| Beta (β) motor neuron | Aβ | ||||
| Gamma (γ) motor neuron | Aγ | 5-8 | Yes | 4–24[46][47] | Intrafusal muscle fibers |
Sensory[edit]
Different sensory receptors innervate different types of nerve fibers. Proprioceptors are innervated by type Ia, Ib and II sensory fibers, mechanoreceptors by type II and III sensory fibers and nociceptors and thermoreceptors by type III and IV sensory fibers.
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin | Conduction velocity (m/s) |
Associated sensory receptors | Proprioceptors | Mechanoceptors | Nociceptors and thermoreceptors |
|---|---|---|---|---|---|---|---|---|
| Ia | Aα | 13–20 | Yes | 80–120 | Primary receptors of muscle spindle (annulospiral ending) | ✔ | ||
| Ib | Aα | 13–20 | Yes | 80–120 | Golgi tendon organ | |||
| II | Aβ | 6–12 | Yes | 33–75 | Secondary receptors of muscle spindle (flower-spray ending). All cutaneous mechanoreceptors |
✔ | ||
| III | Aδ | 1–5 | Thin | 3–30 | Free nerve endings of touch and pressure Nociceptors of lateral spinothalamic tract Cold thermoreceptors |
✔ | ||
| IV | C | 0.2–1.5 | No | 0.5–2.0 | Nociceptors of anterior spinothalamic tract Warmth receptors |
Autonomic[edit]
The autonomic nervous system has two kinds of peripheral fibers:
| Type | Erlanger-Gasser Classification |
Diameter (µm) |
Myelin[48] | Conduction velocity (m/s) |
|---|---|---|---|---|
| preganglionic fibers | B | 1–5 | Yes | 3–15 |
| postganglionic fibers | C | 0.2–1.5 | No | 0.5–2.0 |
Clinical significance[edit]
In order of degree of severity, injury to a nerve can be described as neurapraxia, axonotmesis, or neurotmesis.
Concussion is considered a mild form of diffuse axonal injury.[49] Axonal injury can also cause central chromatolysis. The dysfunction of axons in the nervous system is one of the major causes of many inherited neurological disorders that affect both peripheral and central neurons.[5]
When an axon is crushed, an active process of axonal degeneration takes place at the part of the axon furthest from the cell body. This degeneration takes place quickly following the injury, with the part of the axon being sealed off at the membranes and broken down by macrophages. This is known as Wallerian degeneration.[50] Dying back of an axon can also take place in many neurodegenerative diseases, particularly when axonal transport is impaired, this is known as Wallerian-like degeneration.[51] Studies suggest that the degeneration happens as
a result of the axonal protein NMNAT2, being prevented from reaching all of the axon.[52]
Demyelination of axons causes the multitude of neurological symptoms found in the disease multiple sclerosis.
Dysmyelination is the abnormal formation of the myelin sheath. This is implicated in several leukodystrophies, and also in schizophrenia.[53][54][55]
A severe traumatic brain injury can result in widespread lesions to nerve tracts damaging the axons in a condition known as diffuse axonal injury. This can lead to a persistent vegetative state.[56] It has been shown in studies on the rat that axonal damage from a single mild traumatic brain injury, can leave a susceptibility to further damage, after repeated mild traumatic brain injuries.[57]
A nerve guidance conduit is an artificial means of guiding axon growth to enable neuroregeneration, and is one of the many treatments used for different kinds of nerve injury.
History[edit]
German anatomist Otto Friedrich Karl Deiters is generally credited with the discovery of the axon by distinguishing it from the dendrites.[5] Swiss Rüdolf Albert von Kölliker and German Robert Remak were the first to identify and characterize the axon initial segment. Kölliker named the axon in 1896.[58] Louis-Antoine Ranvier was the first to describe the gaps or nodes found on axons and for this contribution these axonal features are now commonly referred to as the nodes of Ranvier. Santiago Ramón y Cajal, a Spanish anatomist, proposed that axons were the output components of neurons, describing their functionality.[5] Joseph Erlanger and Herbert Gasser earlier developed the classification system for peripheral nerve fibers,[59] based on axonal conduction velocity, myelination, fiber size etc. Alan Hodgkin and Andrew Huxley also employed the squid giant axon (1939) and by 1952 they had obtained a full quantitative description of the ionic basis of the action potential, leading to the formulation of the Hodgkin–Huxley model. Hodgkin and Huxley were awarded jointly the Nobel Prize for this work in 1963. The formulae detailing axonal conductance were extended to vertebrates in the Frankenhaeuser–Huxley equations. The understanding of the biochemical basis for action potential propagation has advanced further, and includes many details about individual ion channels.
Other animals[edit]
The axons in invertebrates have been extensively studied. The longfin inshore squid, often used as a model organism has the longest known axon.[60] The giant squid has the largest axon known. Its size ranges from 0.5 (typically) to 1 mm in diameter and is used in the control of its jet propulsion system. The fastest recorded conduction speed of 210 m/s, is found in the ensheathed axons of some pelagic Penaeid shrimps[61] and the usual range is between 90 and 200 meters/s[62] (cf 100–120 m/s for the fastest myelinated vertebrate axon.)
In other cases as seen in rat studies an axon originates from a dendrite; such axons are said to have «dendritic origin». Some axons with dendritic origin similarly have a «proximal» initial segment that starts directly at the axon origin, while others have a «distal» initial segment, discernibly separated from the axon origin.[63] In many species some of the neurons have axons that emanate from the dendrite and not from the cell body, and these are known as axon-carrying dendrites.[1] In many cases, an axon originates at an axon hillock on the soma; such axons are said to have «somatic origin». Some axons with somatic origin have a «proximal» initial segment adjacent the axon hillock, while others have a «distal» initial segment, separated from the soma by an extended axon hillock.[63]
See also[edit]
- Electrophysiology
- Ganglionic eminence
- Giant axonal neuropathy
- Neuronal tracing
- Pioneer axon
References[edit]
- ^ a b Triarhou LC (2014). «Axons emanating from dendrites: phylogenetic repercussions with Cajalian hues». Frontiers in Neuroanatomy. 8: 133. doi:10.3389/fnana.2014.00133. PMC 4235383. PMID 25477788.
- ^ Yau KW (December 1976). «Receptive fields, geometry and conduction block of sensory neurones in the central nervous system of the leech». The Journal of Physiology. 263 (3): 513–38. doi:10.1113/jphysiol.1976.sp011643. PMC 1307715. PMID 1018277.
- ^ a b c Squire, Larry (2013). Fundamental neuroscience (4th ed.). Amsterdam: Elsevier/Academic Press. pp. 61–65. ISBN 978-0-12-385-870-2.
- ^ a b c Luders E, Thompson PM, Toga AW (August 2010). «The development of the corpus callosum in the healthy human brain». The Journal of Neuroscience. 30 (33): 10985–90. doi:10.1523/JNEUROSCI.5122-09.2010. PMC 3197828. PMID 20720105.
- ^ a b c d e Debanne D, Campanac E, Bialowas A, Carlier E, Alcaraz G (April 2011). «Axon physiology» (PDF). Physiological Reviews. 91 (2): 555–602. doi:10.1152/physrev.00048.2009. PMID 21527732. S2CID 13916255.
- ^ Nelson AD, Jenkins PM (2017). «Axonal Membranes and Their Domains: Assembly and Function of the Axon Initial Segment and Node of Ranvier». Frontiers in Cellular Neuroscience. 11: 136. doi:10.3389/fncel.2017.00136. PMC 5422562. PMID 28536506.
- ^ Leterrier C, Clerc N, Rueda-Boroni F, Montersino A, Dargent B, Castets F (2017). «Ankyrin G Membrane Partners Drive the Establishment and Maintenance of the Axon Initial Segment». Frontiers in Cellular Neuroscience. 11: 6. doi:10.3389/fncel.2017.00006. PMC 5266712. PMID 28184187.
- ^ Leterrier C (February 2018). «The Axon Initial Segment: An Updated Viewpoint». The Journal of Neuroscience. 38 (9): 2135–2145. doi:10.1523/jneurosci.1922-17.2018. PMC 6596274. PMID 29378864.
- ^ Rasband MN (August 2010). «The axon initial segment and the maintenance of neuronal polarity». Nature Reviews. Neuroscience. 11 (8): 552–62. doi:10.1038/nrn2852. PMID 20631711. S2CID 23996233.
- ^ a b c d Jones SL, Svitkina TM (2016). «Axon Initial Segment Cytoskeleton: Architecture, Development, and Role in Neuron Polarity». Neural Plasticity. 2016: 6808293. doi:10.1155/2016/6808293. PMC 4967436. PMID 27493806.
- ^ Clark BD, Goldberg EM, Rudy B (December 2009). «Electrogenic tuning of the axon initial segment». The Neuroscientist. 15 (6): 651–68. doi:10.1177/1073858409341973. PMC 2951114. PMID 20007821.
- ^ a b Yamada R, Kuba H (2016). «Structural and Functional Plasticity at the Axon Initial Segment». Frontiers in Cellular Neuroscience. 10: 250. doi:10.3389/fncel.2016.00250. PMC 5078684. PMID 27826229.
- ^ a b Susuki K, Kuba H (March 2016). «Activity-dependent regulation of excitable axonal domains». The Journal of Physiological Sciences. 66 (2): 99–104. doi:10.1007/s12576-015-0413-4. PMID 26464228. S2CID 18862030.
- ^ a b c d e Alberts B (2004). Essential cell biology: an introduction to the molecular biology of the cell (2nd ed.). New York: Garland. pp. 584–587. ISBN 978-0-8153-3481-1.
- ^ a b Alberts B (2002). Molecular biology of the cell (4th ed.). New York: Garland. pp. 979–981. ISBN 978-0-8153-4072-0.
- ^ Ozgen, H; Baron, W; Hoekstra, D; Kahya, N (September 2016). «Oligodendroglial membrane dynamics in relation to myelin biogenesis». Cellular and Molecular Life Sciences. 73 (17): 3291–310. doi:10.1007/s00018-016-2228-8. PMC 4967101. PMID 27141942.
- ^ Sadler, T. (2010). Langman’s medical embryology (11th ed.). Philadelphia: Lippincott William & Wilkins. p. 300. ISBN 978-0-7817-9069-7.
- ^ Hess A, Young JZ (November 1952). «The nodes of Ranvier». Proceedings of the Royal Society of London. Series B, Biological Sciences. Series B. 140 (900): 301–20. Bibcode:1952RSPSB.140..301H. doi:10.1098/rspb.1952.0063. JSTOR 82721. PMID 13003931. S2CID 11963512.
- ^ Robbins AA, Fox SE, Holmes GL, Scott RC, Barry JM (November 2013). «Short duration waveforms recorded extracellularly from freely moving rats are representative of axonal activity». Frontiers in Neural Circuits. 7 (181): 181. doi:10.3389/fncir.2013.00181. PMC 3831546. PMID 24348338.
- ^ Rongjing Ge, Hao Qian and Jin-Hui Wang* (2011) Molecular Brain 4(19), 1~11
- ^ Rongjing Ge, Hao Qian, Na Chen and Jin-Hui Wang* (2014) Molecular Brain 7(26):1-16
- ^ Chen N, Yu J, Qian H, Ge R, Wang JH (July 2010). «Axons amplify somatic incomplete spikes into uniform amplitudes in mouse cortical pyramidal neurons». PLOS ONE. 5 (7): e11868. Bibcode:2010PLoSO…511868C. doi:10.1371/journal.pone.0011868. PMC 2912328. PMID 20686619.
- ^ Wolpert, Lewis (2015). Principles of development (5th ed.). pp. 520–524. ISBN 978-0-19-967814-3.
- ^ Fletcher TL, Banker GA (December 1989). «The establishment of polarity by hippocampal neurons: the relationship between the stage of a cell’s development in situ and its subsequent development in culture». Developmental Biology. 136 (2): 446–54. doi:10.1016/0012-1606(89)90269-8. PMID 2583372.
- ^ Jiang H, Rao Y (May 2005). «Axon formation: fate versus growth». Nature Neuroscience. 8 (5): 544–6. doi:10.1038/nn0505-544. PMID 15856056. S2CID 27728967.
- ^ Goslin K, Banker G (April 1989). «Experimental observations on the development of polarity by hippocampal neurons in culture». The Journal of Cell Biology. 108 (4): 1507–16. doi:10.1083/jcb.108.4.1507. PMC 2115496. PMID 2925793.
- ^ Lamoureux P, Ruthel G, Buxbaum RE, Heidemann SR (November 2002). «Mechanical tension can specify axonal fate in hippocampal neurons». The Journal of Cell Biology. 159 (3): 499–508. doi:10.1083/jcb.200207174. PMC 2173080. PMID 12417580.
- ^ a b Arimura N, Kaibuchi K (March 2007). «Neuronal polarity: from extracellular signals to intracellular mechanisms». Nature Reviews. Neuroscience. 8 (3): 194–205. doi:10.1038/nrn2056. PMID 17311006. S2CID 15556921.
- ^ Neuroglia and pioneer neurons express UNC-6 to provide global and local netrin cues for guiding migrations in C. elegans
- ^ Serafini T, Kennedy TE, Galko MJ, Mirzayan C, Jessell TM, Tessier-Lavigne M (August 1994). «The netrins define a family of axon outgrowth-promoting proteins homologous to C. elegans UNC-6». Cell. 78 (3): 409–24. doi:10.1016/0092-8674(94)90420-0. PMID 8062384. S2CID 22666205.
- ^ Hong K, Hinck L, Nishiyama M, Poo MM, Tessier-Lavigne M, Stein E (June 1999). «A ligand-gated association between cytoplasmic domains of UNC5 and DCC family receptors converts netrin-induced growth cone attraction to repulsion». Cell. 97 (7): 927–41. doi:10.1016/S0092-8674(00)80804-1. PMID 10399920. S2CID 18043414.
- ^ Hedgecock EM, Culotti JG, Hall DH (January 1990). «The unc-5, unc-6, and unc-40 genes guide circumferential migrations of pioneer axons and mesodermal cells on the epidermis in C. elegans». Neuron. 4 (1): 61–85. doi:10.1016/0896-6273(90)90444-K. PMID 2310575. S2CID 23974242.
- ^ Huang EJ, Reichardt LF (2003). «Trk receptors: roles in neuronal signal transduction». Annual Review of Biochemistry. 72: 609–42. doi:10.1146/annurev.biochem.72.121801.161629. PMID 12676795. S2CID 10217268.
- ^ a b Da Silva JS, Hasegawa T, Miyagi T, Dotti CG, Abad-Rodriguez J (May 2005). «Asymmetric membrane ganglioside sialidase activity specifies axonal fate». Nature Neuroscience. 8 (5): 606–15. doi:10.1038/nn1442. PMID 15834419. S2CID 25227765.
- ^ Bradke F, Dotti CG (March 1999). «The role of local actin instability in axon formation». Science. 283 (5409): 1931–4. Bibcode:1999Sci…283.1931B. doi:10.1126/science.283.5409.1931. PMID 10082468.
- ^ Furley AJ, Morton SB, Manalo D, Karagogeos D, Dodd J, Jessell TM (April 1990). «The axonal glycoprotein TAG-1 is an immunoglobulin superfamily member with neurite outgrowth-promoting activity». Cell. 61 (1): 157–70. doi:10.1016/0092-8674(90)90223-2. PMID 2317872. S2CID 28813676.
- ^ Alberts, Bruce (2015). Molecular biology of the cell (Sixth ed.). p. 947. ISBN 9780815344643.
- ^ Kunik D, Dion C, Ozaki T, Levin LA, Costantino S (2011). «Laser-based single-axon transection for high-content axon injury and regeneration studies». PLOS ONE. 6 (11): e26832. Bibcode:2011PLoSO…626832K. doi:10.1371/journal.pone.0026832. PMC 3206876. PMID 22073205.
- ^ Schwab ME (February 2004). «Nogo and axon regeneration». Current Opinion in Neurobiology. 14 (1): 118–24. doi:10.1016/j.conb.2004.01.004. PMID 15018947. S2CID 9672315.
- ^ Gensel JC, Nakamura S, Guan Z, van Rooijen N, Ankeny DP, Popovich PG (March 2009). «Macrophages promote axon regeneration with concurrent neurotoxicity». The Journal of Neuroscience. 29 (12): 3956–68. doi:10.1523/JNEUROSCI.3992-08.2009. PMC 2693768. PMID 19321792.
- ^ Myers KA, Baas PW (September 2007). «Kinesin-5 regulates the growth of the axon by acting as a brake on its microtubule array». The Journal of Cell Biology. 178 (6): 1081–91. doi:10.1083/jcb.200702074. PMC 2064629. PMID 17846176.
- ^ Rishal I, Kam N, Perry RB, Shinder V, Fisher EM, Schiavo G, Fainzilber M (June 2012). «A motor-driven mechanism for cell-length sensing». Cell Reports. 1 (6): 608–16. doi:10.1016/j.celrep.2012.05.013. PMC 3389498. PMID 22773964.
- ^ Karamched BR, Bressloff PC (May 2015). «Delayed feedback model of axonal length sensing». Biophysical Journal. 108 (9): 2408–19. Bibcode:2015BpJ…108.2408K. doi:10.1016/j.bpj.2015.03.055. PMC 4423051. PMID 25954897.
- ^ Bressloff PC, Karamched BR (2015). «A frequency-dependent decoding mechanism for axonal length sensing». Frontiers in Cellular Neuroscience. 9: 281. doi:10.3389/fncel.2015.00281. PMC 4508512. PMID 26257607.
- ^ Folz F, Wettmann L, Morigi G, Kruse K (May 2019). «Sound of an axon’s growth». Physical Review E. 99 (5–1): 050401. arXiv:1807.04799. Bibcode:2019PhRvE..99e0401F. doi:10.1103/PhysRevE.99.050401. PMID 31212501. S2CID 118682719.
- ^ Andrew BL, Part NJ (April 1972). «Properties of fast and slow motor units in hind limb and tail muscles of the rat». Quarterly Journal of Experimental Physiology and Cognate Medical Sciences. 57 (2): 213–25. doi:10.1113/expphysiol.1972.sp002151. PMID 4482075.
- ^ Russell NJ (January 1980). «Axonal conduction velocity changes following muscle tenotomy or deafferentation during development in the rat». The Journal of Physiology. 298: 347–60. doi:10.1113/jphysiol.1980.sp013085. PMC 1279120. PMID 7359413.
- ^ Pocock G, Richards CD, et al. (2004). Human Physiology (2nd ed.). New York: Oxford University Press. pp. 187–189. ISBN 978-0-19-858527-5.
- ^ Dawodu ST (16 August 2017). «Traumatic Brain Injury (TBI) — Definition, Epidemiology, Pathophysiology». Medscape. Archived from the original on 12 June 2018. Retrieved 14 July 2018.
- ^ Trauma and Wallerian Degeneration Archived 2 May 2006 at the Wayback Machine, University of California, San Francisco
- ^ Coleman MP, Freeman MR (1 June 2010). «Wallerian degeneration, wld(s), and nmnat». Annual Review of Neuroscience. 33 (1): 245–67. doi:10.1146/annurev-neuro-060909-153248. PMC 5223592. PMID 20345246.
- ^ Gilley J, Coleman MP (January 2010). «Endogenous Nmnat2 is an essential survival factor for maintenance of healthy axons». PLOS Biology. 8 (1): e1000300. doi:10.1371/journal.pbio.1000300. PMC 2811159. PMID 20126265.
- ^ Krämer-Albers EM, Gehrig-Burger K, Thiele C, Trotter J, Nave KA (November 2006). «Perturbed interactions of mutant proteolipid protein/DM20 with cholesterol and lipid rafts in oligodendroglia: implications for dysmyelination in spastic paraplegia». The Journal of Neuroscience. 26 (45): 11743–52. doi:10.1523/JNEUROSCI.3581-06.2006. PMC 6674790. PMID 17093095.
- ^ Matalon R, Michals-Matalon K, Surendran S, Tyring SK (2006). «Canavan disease: studies on the knockout mouse». N-Acetylaspartate. Adv. Exp. Med. Biol. Advances in Experimental Medicine and Biology. Vol. 576. pp. 77–93, discussion 361–3. doi:10.1007/0-387-30172-0_6. ISBN 978-0-387-30171-6. PMID 16802706. S2CID 44405442.
- ^ Tkachev D, Mimmack ML, Huffaker SJ, Ryan M, Bahn S (August 2007). «Further evidence for altered myelin biosynthesis and glutamatergic dysfunction in schizophrenia». The International Journal of Neuropsychopharmacology. 10 (4): 557–63. doi:10.1017/S1461145706007334. PMID 17291371.
- ^ «Brain Injury, Traumatic». Medcyclopaedia. GE. Archived from the original on 26 May 2011. Retrieved 20 June 2018.
- ^ Wright DK, Brady RD, Kamnaksh A, Trezise J, Sun M, McDonald SJ, et al. (October 2019). «Repeated mild traumatic brain injuries induce persistent changes in plasma protein and magnetic resonance imaging biomarkers in the rat». Scientific Reports. 9 (1): 14626. Bibcode:2019NatSR…914626W. doi:10.1038/s41598-019-51267-w. PMC 6787341. PMID 31602002.
- ^ Finger S (1994). Origins of neuroscience: a history of explorations into brain function. Oxford University Press. p. 47. ISBN 9780195146943. OCLC 27151391.
Kölliker would give the «axon» its name in 1896.
- ^ Grant G (December 2006). «The 1932 and 1944 Nobel Prizes in physiology or medicine: rewards for ground-breaking studies in neurophysiology». Journal of the History of the Neurosciences. 15 (4): 341–57. doi:10.1080/09647040600638981. PMID 16997762. S2CID 37676544.
- ^ Hellier, Jennifer L. (16 December 2014). The Brain, the Nervous System, and Their Diseases [3 volumes]. ABC-CLIO. ISBN 9781610693387. Archived from the original on 14 March 2018.
- ^ Hsu K, Terakawa S (July 1996). «Fenestration in the myelin sheath of nerve fibers of the shrimp: a novel node of excitation for saltatory conduction». Journal of Neurobiology. 30 (3): 397–409. doi:10.1002/(SICI)1097-4695(199607)30:3<397::AID-NEU8>3.0.CO;2-#. PMID 8807532.
- ^ Salzer JL, Zalc B (October 2016). «Myelination». Current Biology. 26 (20): R971–R975. doi:10.1016/j.cub.2016.07.074. PMID 27780071.
- ^ a b Höfflin F, Jack A, Riedel C, Mack-Bucher J, Roos J, Corcelli C, et al. (2017). «Heterogeneity of the Axon Initial Segment in Interneurons and Pyramidal Cells of Rodent Visual Cortex». Frontiers in Cellular Neuroscience. 11: 332. doi:10.3389/fncel.2017.00332. PMC 5684645. PMID 29170630.
External links[edit]
- Histology image: 3_09 at the University of Oklahoma Health Sciences Center – «Slide 3 Spinal cord»
В предыдущей главе мы ознакомились с такими понятиями, как искусственный интеллект, машинное обучение и искусственные нейронные сети.
В этой главе я детально опишу модель искусственного нейрона, расскажу о подходах к обучению сети, а также опишу некоторые известные виды искусственных нейронных сетей, которые мы будем изучать в следующих главах.
Упрощение
В прошлой главе я постоянно говорил о каких-то серьезных упрощениях. Причина упрощений заключается в том, что никакие современные компьютеры не могут быстро моделировать такие сложные системы, как наш мозг. К тому же, как я уже говорил, наш мозг переполнен различными биологическими механизмами, не относящиеся к обработке информации.
Нам нужна модель преобразования входного сигнала в нужный нам выходной. Все остальное нас не волнует. Начинаем упрощать.
Биологическая структура → схема
В предыдущей главе вы поняли, насколько сложно устроены биологические нейронные сети и биологические нейроны. Вместо изображения нейронов в виде чудовищ с щупальцами давайте просто будем рисовать схемы.
Вообще говоря, есть несколько способов графического изображения нейронных сетей и нейронов. Здесь мы будем изображать искусственные нейроны в виде кружков.
Вместо сложного переплетения входов и выходов будем использовать стрелки, обозначающие направление движения сигнала.
Таким образом искусственная нейронная сеть может быть представлена в виде совокупности кружков (искусственных нейронов), связанных стрелками.
Электрические сигналы → числа
В реальной биологической нейронной сети от входов сети к выходам передается электрический сигнал. В процессе прохода по нейронной сети он может изменяться.
Электрический сигнал всегда будет электрическим сигналом. Концептуально ничего не изменяется. Но что же тогда меняется? Меняется величина этого электрического сигнала (сильнее/слабее). А любую величину всегда можно выразить числом (больше/меньше).
В нашей модели искусственной нейронной сети нам совершенно не нужно реализовывать поведение электрического сигнала, так как от его реализации все равно ничего зависеть не будет.
На входы сети мы будем подавать какие-то числа, символизирующие величины электрического сигнала, если бы он был. Эти числа будут продвигаться по сети и каким-то образом меняться. На выходе сети мы получим какое-то результирующее число, являющееся откликом сети.
Для удобства все равно будем называть наши числа, циркулирующие в сети, сигналами.
Синапсы → веса связей
Вспомним картинку из первой главы, на которой цветом были изображены связи между нейронами – синапсы. Синапсы могут усиливать или ослаблять проходящий по ним электрический сигнал.
Давайте характеризовать каждую такую связь определенным числом, называемым весом данной связи. Сигнал, прошедший через данную связь, умножается на вес соответствующей связи.
Это ключевой момент в концепции искусственных нейронных сетей, я объясню его подробнее. Посмотрите на картинку ниже. Теперь каждой черной стрелке (связи) на этой картинке соответствует некоторое число ( w_i ) (вес связи). И когда сигнал проходит по этой связи, его величина умножается на вес этой связи.
На приведенном выше рисунке вес стоит не у каждой связи лишь потому, что там нет места для обозначений. В реальности у каждой ( i )-ой связи свой собственный ( w_i )-ый вес.
Искусственный нейрон
Теперь мы переходим к рассмотрению внутренней структуры искусственного нейрона и того, как он преобразует поступающий на его входы сигнал.
На рисунке ниже представлена полная модель искусственного нейрона.
Не пугайтесь, ничего сложного здесь нет. Давайте рассмотрим все подробно слева направо.
Входы, веса и сумматор
У каждого нейрона, в том числе и у искусственного, должны быть какие-то входы, через которые он принимает сигнал. Мы уже вводили понятие весов, на которые умножаются сигналы, проходящие по связи. На картинке выше веса изображены кружками.
Поступившие на входы сигналы умножаются на свои веса. Сигнал первого входа ( x_1 ) умножается на соответствующий этому входу вес ( w_1 ). В итоге получаем ( x_1w_1 ). И так до ( n )-ого входа. В итоге на последнем входе получаем ( x_nw_n ).
Теперь все произведения передаются в сумматор. Уже исходя из его названия можно понять, что он делает. Он просто суммирует все входные сигналы, умноженные на соответствующие веса:
[ x_1w_1+x_2w_2+cdots+x_nw_n = sumlimits^n_{i=1}x_iw_i ]
Результатом работы сумматора является число, называемое взвешенной суммой.
Взвешенная сумма (Weighted sum) (( net )) — сумма входных сигналов, умноженных на соответствующие им веса.
[ net=sumlimits^n_{i=1}x_iw_i ]
Роль сумматора очевидна – он агрегирует все входные сигналы (которых может быть много) в какое-то одно число – взвешенную сумму, которая характеризует поступивший на нейрон сигнал в целом. Еще взвешенную сумму можно представить как степень общего возбуждения нейрона.
Пример
Для понимания роли последнего компонента искусственного нейрона – функции активации – я приведу аналогию.
Давайте рассмотрим один искусственный нейрон. Его задача – решить, ехать ли отдыхать на море. Для этого на его входы мы подаем различные данные. Пусть у нашего нейрона будет 4 входа:
- Стоимость поездки
- Какая на море погода
- Текущая обстановка с работой
- Будет ли на пляже закусочная
Все эти параметры будем характеризовать 0 или 1. Соответственно, если погода на море хорошая, то на этот вход подаем 1. И так со всеми остальными параметрами.
Если у нейрона есть четыре входа, то должно быть и четыре весовых коэффициента. В нашем примере весовые коэффициенты можно представить как показатели важности каждого входа, влияющие на общее решение нейрона. Веса входов распределим следующим образом:
- 5
- 4
- 1
- 1
Нетрудно заметить, что очень большую роль играют факторы стоимости и погоды на море (первые два входа). Они же и будут играть решающую роль при принятии нейроном решения.
Пусть на входы нашего нейрона мы подаем следующие сигналы:
- 1
- 0
- 0
- 1
Умножаем веса входов на сигналы соответствующих входов:
- 5
- 0
- 0
- 1
Взвешенная сумма для такого набора входных сигналов равна 6:
[ net=sumlimits^4_{i=1}x_iw_i = 5 + 0 + 0 + 1 =6 ]
Все классно, но что делать дальше? Как нейрон должен решить, ехать на море или нет? Очевидно, нам нужно как-то преобразовать нашу взвешенную сумму и получить ответ.
Вот на сцену выходит функция активации.
Функция активации
Просто так подавать взвешенную сумму на выход достаточно бессмысленно. Нейрон должен как-то обработать ее и сформировать адекватный выходной сигнал. Именно для этих целей и используют функцию активации.
Она преобразует взвешенную сумму в какое-то число, которое и является выходом нейрона (выход нейрона обозначим переменной ( out )).
Для разных типов искусственных нейронов используют самые разные функции активации. В общем случае их обозначают символом ( phi(net) ). Указание взвешенного сигнала в скобках означает, что функция активации принимает взвешенную сумму как параметр.
Функция активации (Activation function) (( phi(net) )) — функция, принимающая взвешенную сумму как аргумент. Значение этой функции и является выходом нейрона (( out )).
[ out=phi(net) ]
Далее мы подробно рассмотрим самые известные функции активации.
Функция единичного скачка
Самый простой вид функции активации. Выход нейрона может быть равен только 0 или 1. Если взвешенная сумма больше определенного порога ( b ), то выход нейрона равен 1. Если ниже, то 0.
Как ее можно использовать? Предположим, что мы поедем на море только тогда, когда взвешенная сумма больше или равна 5. Значит наш порог равен 5:
[ b=5 ]
В нашем примере взвешенная сумма равнялась 6, а значит выходной сигнал нашего нейрона равен 1. Итак, мы едем на море.
Однако если бы погода на море была бы плохой, а также поездка была бы очень дорогой, но имелась бы закусочная и обстановка с работой нормальная (входы: 0011), то взвешенная сумма равнялась бы 2, а значит выход нейрона равнялся бы 0. Итак, мы никуда не едем.
В общем, нейрон смотрит на взвешенную сумму и если она получается больше его порога, то нейрон выдает выходной сигнал, равный 1.
Графически эту функцию активации можно изобразить следующим образом.
На горизонтальной оси расположены величины взвешенной суммы. На вертикальной оси — значения выходного сигнала. Как легко видеть, возможны только два значения выходного сигнала: 0 или 1. Причем 0 будет выдаваться всегда от минус бесконечности и вплоть до некоторого значения взвешенной суммы, называемого порогом. Если взвешенная сумма равна порогу или больше него, то функция выдает 1. Все предельно просто.
Теперь запишем эту функцию активации математически. Почти наверняка вы сталкивались с таким понятием, как составная функция. Это когда мы под одной функцией объединяем несколько правил, по которым рассчитывается ее значение. В виде составной функции функция единичного скачка будет выглядеть следующим образом:
[ out(net) = begin{cases} 0, net < b \ 1, net geq b end{cases} ]
В этой записи нет ничего сложного. Выход нейрона (( out )) зависит от взвешенной суммы (( net )) следующим образом: если ( net ) (взвешенная сумма) меньше какого-то порога (( b )), то ( out ) (выход нейрона) равен 0. А если ( net ) больше или равен порогу ( b ), то ( out ) равен 1.
Сигмоидальная функция
На самом деле существует целое семейство сигмоидальных функций, некоторые из которых применяют в качестве функции активации в искусственных нейронах.
Все эти функции обладают некоторыми очень полезными свойствами, ради которых их и применяют в нейронных сетях. Эти свойства станут очевидными после того, как вы увидите графики этих функций.
Итак… самая часто используемая в нейронных сетях сигмоида — логистическая функция.
График этой функции выглядит достаточно просто. Если присмотреться, то можно увидеть некоторое подобие английской буквы ( S ), откуда и пошло название семейства этих функций.
А вот так она записывается аналитически:
[ out(net)=frac{1}{1+exp(-a cdot net)} ]
Что за параметр ( a )? Это какое-то число, которое характеризует степень крутизны функции. Ниже представлены логистические функции с разным параметром ( a ).
Вспомним наш искусственный нейрон, определяющий, надо ли ехать на море. В случае с функцией единичного скачка все было очевидно. Мы либо едем на море (1), либо нет (0).
Здесь же случай более приближенный к реальности. Мы до конца полностью не уверены (в особенности, если вы параноик) – стоит ли ехать? Тогда использование логистической функции в качестве функции активации приведет к тому, что вы будете получать цифру между 0 и 1. Причем чем больше взвешенная сумма, тем ближе выход будет к 1 (но никогда не будет точно ей равен). И наоборот, чем меньше взвешенная сумма, тем ближе выход нейрона будет к 0.
Например, выход нашего нейрона равен 0.8. Это значит, что он считает, что поехать на море все-таки стоит. Если бы его выход был бы равен 0.2, то это означает, что он почти наверняка против поездки на море.
Какие же замечательные свойства имеет логистическая функция?
- она является «сжимающей» функцией, то есть вне зависимости от аргумента (взвешенной суммы), выходной сигнал всегда будет в пределах от 0 до 1
- она более гибкая, чем функция единичного скачка – ее результатом может быть не только 0 и 1, но и любое число между ними
- во всех точках она имеет производную, и эта производная может быть выражена через эту же функцию
Именно из-за этих свойств логистическая функция чаще всего используются в качестве функции активации в искусственных нейронах.
Гиперболический тангенс
Однако есть и еще одна сигмоида – гиперболический тангенс. Он применяется в качестве функции активации биологами для более реалистичной модели нервной клетки.
Такая функция позволяет получить на выходе значения разных знаков (например, от -1 до 1), что может быть полезным для ряда сетей.
Функция записывается следующим образом:
[ out(net) = tanhleft(frac{net}{a}right) ]
В данной выше формуле параметр ( a ) также определяет степень крутизны графика этой функции.
А вот так выглядит график этой функции.
Как видите, он похож на график логистической функции. Гиперболический тангенс обладает всеми полезными свойствами, которые имеет и логистическая функция.
Что мы узнали?
Теперь вы получили полное представление о внутренней структуре искусственного нейрона. Я еще раз приведу краткое описание его работы.
У нейрона есть входы. На них подаются сигналы в виде чисел. Каждый вход имеет свой вес (тоже число). Сигналы на входе умножаются на соответствующие веса. Получаем набор «взвешенных» входных сигналов.
Далее этот набор попадает в сумматор, которой просто складывает все входные сигналы, помноженные на веса. Получившееся число называют взвешенной суммой.
Затем взвешенная сумма преобразуется функцией активации и мы получаем выход нейрона.
Сформулируем теперь самое короткое описание работы нейрона – его математическую модель:
Математическая модель искусственного нейрона с ( n ) входами:
[ out=phileft(sumlimits^n_{i=1}x_iw_iright) ]
где
( phi ) – функция активации
( sumlimits^n_{i=1}x_iw_i ) – взвешенная сумма, как сумма ( n ) произведений входных сигналов на соответствующие веса.
Виды ИНС
Мы разобрались со структурой искусственного нейрона. Искусственные нейронные сети состоят из совокупности искусственных нейронов. Возникает логичный вопрос – а как располагать/соединять друг с другом эти самые искусственные нейроны?
Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу – распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений.
А дальше начинаются различия…
Однослойные нейронные сети
В однослойных нейронных сетях сигналы с входного слоя сразу подаются на выходной слой. Он производит необходимые вычисления, результаты которых сразу подаются на выходы.
Выглядит однослойная нейронная сеть следующим образом:
На этой картинке входной слой обозначен кружками (он не считается за слой нейронной сети), а справа расположен слой обычных нейронов.
Нейроны соединены друг с другом стрелками. Над стрелками расположены веса соответствующих связей (весовые коэффициенты).
Однослойная нейронная сеть (Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.
Многослойные нейронные сети
Такие сети, помимо входного и выходного слоев нейронов, характеризуются еще и скрытым слоем (слоями). Понять их расположение просто – эти слои находятся между входным и выходным слоями.
Такая структура нейронных сетей копирует многослойную структуру определенных отделов мозга.
Название скрытый слой получил неслучайно. Дело в том, что только относительно недавно были разработаны методы обучения нейронов скрытого слоя. До этого обходились только однослойными нейросетями.
Многослойные нейронные сети обладают гораздо большими возможностями, чем однослойные.
Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.
Многослойная нейронная сеть (Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.
Сети прямого распространения
Можно заметить одну очень интересную деталь на картинках нейросетей в примерах выше.
Во всех примерах стрелки строго идут слева направо, то есть сигнал в таких сетях идет строго от входного слоя к выходному.
Сети прямого распространения (Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.
Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.
Однако никто не запрещает сигналу идти и в обратную сторону.
Сети с обратными связями
В сетях такого типа сигнал может идти и в обратную сторону. В чем преимущество?
Дело в том, что в сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах.
А в сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).
Возможность сигналов циркулировать в сети открывает новые, удивительные возможности нейронных сетей. С помощью таких сетей можно создавать нейросети, восстанавливающие или дополняющие сигналы. Другими словами такие нейросети имеют свойства кратковременной памяти (как у человека).
Сети с обратными связями (Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.
Обучение нейронной сети
Теперь давайте чуть более подробно рассмотрим вопрос обучения нейронной сети. Что это такое? И каким образом это происходит?
Что такое обучение сети?
Искусственная нейронная сеть – это совокупность искусственных нейронов. Теперь давайте возьмем, например, 100 нейронов и соединим их друг с другом. Ясно, что при подаче сигнала на вход, мы получим что-то бессмысленное на выходе.
Значит нам надо менять какие-то параметры сети до тех пор, пока входной сигнал не преобразуется в нужный нам выходной.
Что мы можем менять в нейронной сети?
Изменять общее количество искусственных нейронов бессмысленно по двум причинам. Во-первых, увеличение количества вычислительных элементов в целом лишь делает систему тяжеловеснее и избыточнее. Во-вторых, если вы соберете 1000 дураков вместо 100, то они все-равно не смогут правильно ответить на вопрос.
Сумматор изменить не получится, так как он выполняет одну жестко заданную функцию – складывать. Если мы его заменим на что-то или вообще уберем, то это вообще уже не будет искусственным нейроном.
Если менять у каждого нейрона функцию активации, то мы получим слишком разношерстную и неконтролируемую нейронную сеть. К тому же, в большинстве случаев нейроны в нейронных сетях одного типа. То есть они все имеют одну и ту же функцию активации.
Остается только один вариант – менять веса связей.
Обучение нейронной сети (Training) — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.
Такой подход к термину «обучение нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей. Каждая из них в отдельности состоит из нейронов одного типа (функция активации одинаковая). Мы обучаемся благодаря изменению синапсов – элементов, которые усиливают/ослабляют входной сигнал.
Однако есть еще один важный момент. Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ». Со стороны будет казаться, что она очень быстро «обучилась». И как только вы подадите немного измененный сигнал, ожидая увидеть правильный ответ, то сеть выдаст бессмыслицу.
В самом деле, зачем нам сеть, определяющая лицо только на одном фото. Мы ждем от сети способности обобщать какие-то признаки и узнавать лица и на других фотографиях тоже.
Именно с этой целью и создаются обучающие выборки.
Обучающая выборка (Training set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.
После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике.
Однако прежде чем пускать свежеиспеченную нейросеть в бой, часто производят оценку качества ее работы на так называемой тестовой выборке.
Тестовая выборка (Testing set) — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.
Мы поняли, что такое «обучение сети» – подбор правильного набора весов. Теперь возникает вопрос – а как можно обучать сеть? В самом общем случае есть два подхода, приводящие к разным результатам: обучение с учителем и обучение без учителя.
Обучение с учителем
Суть данного подхода заключается в том, что вы даете на вход сигнал, смотрите на ответ сети, а затем сравниваете его с уже готовым, правильным ответом.
Важный момент. Не путайте правильные ответы и известный алгоритм решения! Вы можете обвести пальцем лицо на фото (правильный ответ), но не сможете сказать, как это сделали (известный алгоритм). Тут такая же ситуация.
Затем, с помощью специальных алгоритмов, вы меняете веса связей нейронной сети и снова даете ей входной сигнал. Сравниваете ее ответ с правильным и повторяете этот процесс до тех пор, пока сеть не начнет отвечать с приемлемой точностью (как я говорил в 1 главе, однозначно точных ответов сеть давать не может).
Обучение с учителем (Supervised learning) — вид обучения сети, при котором ее веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов.
Где взять правильные ответы?
Если мы хотим, чтобы сеть узнавала лица, мы можем создать обучающую выборку на 1000 фотографий (входные сигналы) и самостоятельно выделить на ней лица (правильные ответы).
Если мы хотим, чтобы сеть прогнозировала рост/падение цен, то обучающую выборку надо делать, основываясь на прошлых данных. В качестве входных сигналов можно брать определенные дни, общее состояние рынка и другие параметры. А в качестве правильных ответов – рост и падение цены в те дни.
И так далее…
Стоит отметить, что учитель, конечно же, не обязательно человек. Дело в том, что порой сеть приходится тренировать часами и днями, совершая тысячи и десятки тысяч попыток. В 99% случаев эту роль выполняет компьютер, а точнее, специальная компьютерная программа.
Обучение без учителя
Обучение без учителя применяют тогда, когда у нас нет правильных ответов на входные сигналы. В этом случае вся обучающая выборка состоит из набора входных сигналов.
Что же происходит при таком обучении сети? Оказывается, что при таком «обучении» сеть начинает выделять классы подаваемых на вход сигналов. Короче говоря – сеть начинает кластеризацию.
Например, вы демонстрируете сети конфеты, пирожные и торты. Вы никак не регулируете работу сети. Вы просто подаете на ее входы данные о данном объекте. Со временем сеть начнет выдавать сигналы трех разных типов, которые и отвечают за объекты на входе.
Обучение без учителя (Unsupervised learning) — вид обучения сети, при котором сеть самостоятельно классифицирует входные сигналы. Правильные (эталонные) выходные сигналы не демонстрируются.
Выводы
В этой главе вы узнали все о структуре искусственного нейрона, а также получили полное представление о том, как он работает (и о его математической модели).
Более того, вы теперь знаете о различных видах искусственных нейронных сетей: однослойные, многослойные, а также feedforward сети и сети с обратными связями.
Вы также ознакомились с тем, что представляет собой обучение сети с учителем и без учителя.
Вы уже знаете необходимую теорию. Последующие главы – рассмотрение конкретных видов нейронных сетей, конкретные алгоритмы их обучения и практика программирования.
Вопросы и задачи
Материал этой главы надо знать очень хорошо, так как в ней содержатся основные теоретические сведения по искусственным нейронным сетям. Обязательно добейтесь уверенных и правильных ответов на все нижеприведенные вопросы и задачи.
Опишите упрощения ИНС по сравнению с биологическими нейросетями.
Из каких элементов состоит искусственный нейрон?
Что такое взвешенная сумма? Какой компонент искусственного нейрона ее вычисляет?
Вычислите взвешенную сумму нейрона (рисунок выше)
Что такое функция активации?
Запишите математическую модель искусственного нейрона.
Чем отличаются однослойные и многослойные нейронные сети?
В чем отличие feedforward сетей от сетей с обратными связями?
Что такое обучающая выборка? В чем ее смысл?
Что понимают под обучением сети?
Что такое обучение с учителем и без него?
Языком у нас будет С#, только потому что я недавно решил его выучить. Я разобрал два наиболее простых примера: однослойный перцептрон Розенблатта, обучаемый коррекцией ошибки, и многослойный перцептрон Румельхарта, обучаемый методом обратного распространения ошибки. Для тех, кому, как и мне, стало интересно, чему они там на самом деле обучились, и насколько они на самом деле способны обобщать – добро пожаловать под кат.
ОСТОРОЖНО! Много картинок. Куски кода.
Для начала хочу предложить вам полюбоваться процессом обучения нейронной сети. Каждый кадр после 1000 учебных точек. Указывается скорость обучения и среднеквадратичная ошибка за эту тысячу циклов.
Из кода я буду показывать только то, что может пригодиться другим желающим сделать всё своими руками или проверить правильность моих выводов. Код важных элементов с корнем выдирается из тестового проекта, в котором он запускался, поэтому где-то могут быть ссылки на элементы, которые я не привожу. Но код при этом работающий, все картинки являются скриншотами из моего учебного проекта.
Для начала нужно выбрать задачу, такую, чтобы на неё глянул, и сразу стало понятно, научился ли перцептрон чему-нибудь и чему. Возьмём две координаты (x и y), и накидаем в них много случайных точек. Это будут входные данные. Нарисуем какой-нибудь график и попросим перцептрон определить, находится точка выше или ниже этого графика. Но перцептрон Розенблатта же у нас работает в целых числах, да и вообще задачка слишком простая. Тогда давайте каждую координату округлим до целого числа и представим в двоичной форме: одна цифра-один вход. Для единообразия во всех примерах рассматривается диапазон координат (0,1), так что перед округлением его надо помножить на максимальное целое значение.
Например, представим каждую координату двухбитным числом. Пара случайных чисел (0.2, 0.7), указывающих на точку выше графика, тогда после округления перейдёт в (1,3) и даст нам следующий учебный пример:
new double[]{0.2, 0.7} => new NeuralTask {
Preview = new double[]{0.25, 0,75, 1},
Input=new double[] {0,1,1,1},
Output=new double[]{1}}
Функция, конвертирующая случайные числа в учебные примеры, выглядит примерно так:
Функция конверсии
var Convertion = (double[] random, double value) => {
var input = new double[]{Math.Floor(random [0]*0x4)/0x4, Math.Floor(random [1]*0x4)/0x4},
byte x = (byte)(input[0] * 4);
byte y = (byte)(input[1] * 4);
int res = (y > value * 4 ? 1 : 0);
return new NeuralTask() {
input = new double[4]{
(x&2)>>1, x&1,
(y&2)>>1, y&1},
output = new double[1] { res },
preview = new double[3] { input[0], input[1], res }
};
};
Тут надо пояснить, что всё это делалось в учебных и исследовательских целях, поэтому не оптимизировалось для скорости и неземной красоты, а где-то писалось так, чтобы удобно было программировать любой мыслимый перцептрон. Поэтому, в частности, входные и выходные данные лежат в double. Получается такая вот простая картинка. Ну, или чуть более сложная, если каждую ось порубить на 256 участков, и функцию взять посложнее:
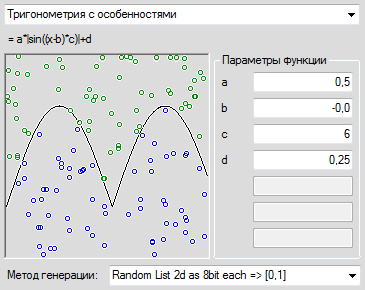
Здесь и далее зелёный цвет – значения больше нуля, тем более насыщенные, чем больше число, красные – значения меньше нуля, синий – значения равные 0 и их ближайшие окрестности.
Исходный код
Сам перцептрон у нас состоит из синапса:
class Synaps
public class Synaps {
private double weight;
/// <summary>Доступатор к одному параметру</summary>
virtual public double Weight {
get { return weight; }
set {
if (weight != value) {
weight = value;
if (axon != null)
ChangeActionPotentialHandler(axon.ActionPotential);
}
}
}
/// <summary>Внутреннее хранилище ссылки на аксон. Возможно, в будущем, в целях оптимизации, разрешим из него читать наследникам, но писать в него точно нельзя.</summary>
private IAxon axon;
// Указание на нейрон, с которого снимается информация.
public IAxon Axon {
get { return axon; }
set { // Вот тут навешиваем обработчики, которые следят за изменением состояния исходного нейрона.
if (axon != null)
axon.RemoveChangeActionPotentialHandler(ChangeActionPotentialHandler);
axon = value;
if (axon != null) {
axon.AddChangeActionPotentialHandler(ChangeActionPotentialHandler);
ChangeActionPotentialHandler(axon.ActionPotential);
}
}
}
public double ActionPotential;
/// <summary> Событие кидается, когда синапс меняет свой потенциал.</summary>
protected Action WhenActionPotentialСhanged;
public void AddActionPotentialChangeHandler(Action handler) {
WhenActionPotentialСhanged += handler;
}
public void RemoveActionPotentialChangeHandler(Action handler) {
WhenActionPotentialСhanged -= handler;
}
virtual protected void ChangeActionPotentialHandler(double axonActionPotential) {
ActionPotential = axonActionPotential * weight; // Проверку на неизменность значения не делаю, потому что она уже есть в нейроне.
if (WhenActionPotentialСhanged != null)
WhenActionPotentialСhanged); // Просто передать событие об изменении потенциала на изучаемом нейроне
}
}
Ничего неожиданного, если не считать, что числа хранятся в double и вместо стандартного события используется кастомное. Теперь нейрон. Нейроны у нас все дружно соответствуют интерфейсу IAxon:
interface IAxon
public interface IAxon {
/// <summary>Значение потенциала действия.</summary>
double ActionPotential { get; }
/// <summary>Более успешной оптимизации не просматривается.</summary>
void AddChangeActionPotentialHandler(Action<double> handler);
void RemoveChangeActionPotentialHandler(Action<double> handler);
/// <summary>Положение, в котором находится аксон в пространстве нейронной сети.</summary>
PointF Position { get; set; }
/// <summary>Имя аксона чтобы идентифицировать его в трейсе.</summary>
string Name { get; set; }
}
Тоже ничего неожиданного, кроме Position, показывающего, где нейрон рисовать.
В качестве входа используются сенсорные нейроны, которым можно задавать значение напрямую:
class SensoryNeuron
public class SensoryNeuron : IAxon {
protected double actionPotential;
public double ActionPotential {
get { return actionPotential; }
set {
if (actionPotential != value) {
actionPotential = value;
if (WhenChangeActionPotential != null)
WhenChangeActionPotential(actionPotential);
}
}
}
}
Наконец, сам нейрон в достаточно обобщённой форме:
class Neuron
/// <summary>Общий предок. Есть только функция активации </summary>
public class Neuron : IAxon {
/// <summary> Список синапсов, с которых получает информацию этот нейрон. Список в виде массива, потому что перебирать массив быстрее, а изменение списка делается редко.</summary>
public Synaps[] Synapses = new Synaps[0];
/// <summary> Внутренний флаг, означающий, что один из синапсов поменял свой потенциал и нейрон нуждается в пересчёте.</summary>
protected bool synapsPotentialChanged = false;
/// <summary> Добавить в нейрон новую синаптическую связь. И нацепить, кроме того, все положенные слушатели. </summary>
public void AppendSinaps(Synaps target) {
// При каждом обновлении пересоздаём массив. Выглядит это, конечно, неоптимально, но эта операция делается очень редко, в отличии от самого вычисления.
Synapses = Synapses.Concat(new Synaps[1] { target }).ToArray();
target.AddActionPotentialChangeHandler(ChangeSynapsPotentialHandler); // Слушатели новые навешать.
synapsPotentialChanged = true;
}
virtual protected void ChangeSynapsPotentialHandler() {
synapsPotentialChanged = true;
}
/// <summary> Функция активации нейрона. Она тут хранится отдельной переменной, чтобы ускорить процесс вызова.</summary>
protected DTransferFunction transferFunctionDelegate;
public virtual DTransferFunction TransferFunction {
get { return transferFunctionDelegate; }
set {
transferFunctionDelegate = value;
}
}
/// <summary> Метод вызывает расчёт в нейроне и может привести к изменению его потенциала действия. </summary>
public virtual void Excitation() {
if (!synapsPotentialChanged) return; // Для нецелочисленного нейрона проверка почти всегда бессмысленна
synapsPotentialChanged = false;
synapsPotentials = 0;
for (int i = 0; i < Synapses.Length; i++)
synapsPotentials += Synapses[i].ActionPotential;
double newValue = transferFunctionDelegate(synapsPotentials);
if (actionPotential != newValue) { // Для некоторых специальных случаев значения могут не отличаться. Например, для целочисленного перцептрона.
actionPotential = newValue;
if (WhenChangeActionPotential != null)
WhenChangeActionPotential(actionPotential);
}
}
}
Здесь:
Функция Активации
/// <summary> Функция определения потенциала действия на основе входных сигналов. </summary>
/// <param name="argument">Сумма потенциалов синапсов</param>
/// <returns>Возвращает значение потенциала действия нейрона</returns>
public delegate double DTransferFunction(double argument);
DTransferFunction BarrierTransferFunction = (double x) => x <= 0 ? 0 : 1;
Наконец из всего этого вместе получается нейронная сеть и алгоритм её обучения:
class NeuralNetwork, PerceptronClassic, ErrorCorrection
abstract public class NeuralNetwork {
/// <summary>Вход нейронной сети</summary>
public SensoryNeuron[] Input = new SensoryNeuron[0];
/// <summary>
/// Все добавленыне в сеть нейроны выстраиваются в этом массиве в том порядке, в котором будут обработаны. Сенсорные нейроны сюда вообще не попадают.
/// Я не закладываю заранее послойность или любой другой предопределённый алгоритм обхода, чтобы конкретная реализация сети могла переопределять порядок обработки по вкусу.
/// </summary>
public Neuron[] ExcitationOrder = new Neuron[0];
/// <summary>Выход нейронной сети</summary>
public Neuron[] Output = new Neuron[0];
/// <summary>Универсальный метод, создающий сеть с указанными в классе параметрами</summary>
/// <param name="input">Количество сенсорных нейронов - входов</param>
/// <param name="output">Количество выходных нейронов реакции</param>
abstract public void create(uint input, uint output);
public void execute(double[] data) {
// Несовпадение размерности входных сигналов и входа сети на данном этапе не проверяем для экономии
for (int i = 0; i < Input.Length && i < data.Length; i++) {
Input[i].ActionPotential = data[i];
}
for (int i = 0; i < ExcitationOrder.Length; i++)
ExcitationOrder[i].Excitation();
}
public double[] Result() {
// return output.Select(s => s.ActionPotential).ToArray(); //TODO Не забыть сравнить с Linq по скорости.
double[] res = new double[Output.Length];
for (int i = 0; i < res.Length; i++)
res[i] = Output[i].ActionPotential;
return res;
}
}
public class PerceptronClassic : NeuralNetwork {
// Насколько в слое больше нейронов, чем входов сети
public int neuronCountsOverSensoric = 15;
//Сколько синапсов у каждого нейрона
public int ANeuronSynapsCount;
// Первый слой нейронов линейного разложения
public Neuron[] Layer;
// Класс собирает перцептрон Ролзенблатта по заданным характеристикам
override public void create(uint inputCount, uint outputCount) {
rnd = rndSeed >= 0 ? new Random(rndSeed) : new Random();
// Сенсорные нейроны
this.Input = new SensoryNeuron[inputCount];
for (int i = 0; i < inputCount; i++)
Input[i] = new SensoryNeuron() {Name = "S" + i};
//Группа нейронов первого слоя - Ассоциативные
Layer = new Neuron[inputCount + neuronCountsOverSensoric];
for (int i = 0; i < Layer.Length; i++) {
// Это сам нейрон
Layer[i] = new RosenblattNeuron();
// А это его случайные необучаемые синапсы первого слоя
SensoryNeuron[] sub = Input.OrderBy((cell) => rnd.NextDouble()).Take(ANeuronSynapsCount).ToArray();
// Их не больше, чем входных сигналов
for (int j = 0; j < sub.Length; j++) {
Synaps s = new Synaps();
s.Axon = sub[j];
s.Weight = rnd.Next(2) * 2 - 1;
Layer[i].AppendSinaps(s);
}
}
// Назвать сообразно месту в системе.
for (int i = 0; i < Layer.Length; i++)
Layer[i].Name = "A" + i;
// Выходные нейроны - Реагирующие элементы
Output = new Neuron[outputCount];
for (int i = 0; i < Output.Length; i++) {
Output[i] = new RosenblattNeuron();
Output[i].Name = "R" + i;
// Их синапсы с каждым из предыдущего слоя
for (int j = 0; j < Layer.Length; j++) {
Synaps s = new Synaps();
s.Axon = Layer[j];
Output[i].AppendSinaps(s); // Начальный вес 0
}
}
// И складываем в кучу обсчитываемых нейронов
int lastIndex = 0;
ExcitationOrder = new Neuron[Layer.Length + Output.Length];
foreach (Neuron cell in Layer)
ExcitationOrder[lastIndex++] = cell;
foreach (Neuron cell in Output)
ExcitationOrder[lastIndex++] = cell;
}
}
/// <summary>Алгоритм обучения коррекцией ошибки.</summary>
public class ErrorCorrection : LearningAlgorythm {
// Метод, описывающий одиночный акт обучения на одном примере
override protected double LearnNet(double[] required) {
double error = 0;
for (int i = 0; i < required.Length && i < net.Output.Length; i++) {
if (required[i] != net.Output[i].ActionPotential) {
error += 1;
// Перебираем все ассоциативные нейроны
for (int j = 0; j < (net as PerceptronClassic).Layer.Length; j++)
// Находим тех из них, кто активировался
if ((net as PerceptronClassic).Layer[j].ActionPotential > 0)
// У всех нейронов второго слоя
foreach (RosenblattNeuron cell in net.Output)
// Изменяем веса всех синапсов, которые указывают на активированный ассоциативный нейрон
// Если правильное решение – дезактивация, то снижаем вес, если активация – повышаем. Вес может стать отрицательным.
cell.Synapses[j].Weight += required[i] <= 0 ? -1 : 1;
}
}
return error;
}
/// <summary>Обучает одному набору от начала и до конца</summary>
public void LearnTasksSet() {
if (data == null) { Console.WriteLine("Источник данных отсутствует"); return; }
data.Reset();
LearnedTaskSetsCount++;
ErrorsInSet = LearnedTasksInSetCount = 0;
int max = 1000;
while (data.MoveNext() && --max >= 0)
LearnCurrentTask();
// На выходе сет не переключается, поэтому статистика остается видна.
}
/// <summary>Обучать всему сету несколько раз или пока сеть не научится.</summary>
/// <param name="loops">Сколько раз прогнать учебный сет</param>
public void LearnSetManyTimesUntilSuccess(int loops) {
for (int i = 0; i < loops; i++) {
LearnTasksSet();
if (ErrorsInSet == 0) {
break;
}
}
}
}
Источник данных является Enumerable<NeuralTask> и при каждом Reset-е переставляет точки в последовательности в произвольном порядке.
Всё готово, можно запускать.
Для простейшей задачки по два бита на ось, чтобы нам повезло найти подходящее сепарабельное разложение, пришлось добавить в слой A на 8 нейронов больше, чем входов – 12 штук. Подходящее разложение обнаружилось с третьей попытки. Перцептрон безошибочно классифицировал все 16 возможных значений.
Тут можно заметить, что возможных значений всего 16, а я сгенерировал больше. Чтобы случайные числа гарантированно покрыли все возможные варианты.
Раз всё так замечательно, давайте перейдём к чуть более сложной задачке, где на каждую ось у нас приходится 256 вариантов значений. Функцию рассмотрим простейшую. Сгенерируем, для начала, 64 точки. В слое нейронов всего на 20 больше, чем входов – 36 штук. И сразу же успех.
И вот теперь мы сделаем самое интересное. Мы возьмём полученную нами сеть и нарисуем на картинке все возможные значения, которые выдаёт сеть во всех точках. И вот тут выяснится самое грустное. Уровень обобщения, достигнутый сетью, не очень то впечатляет.
Оказывается, сеть в весьма общих чертах представляет, какая закономерность скрывается за предоставленными ей точками. Попробуем предоставить сети более полные данные об изучаемой функции. Сгенерируем 256 точек. 36-ти нейронов, как в прошлый раз, уже недостаточно, чтобы сеть смогла натолкнуться на подходящее линейно сепарабельное разложение. Теперь нам потребовалось создать 70 ассоциативных нейронов, прогнать учебный набор задач 615 раз и пропылесосить кулер, чтобы процессор не перегревался от радости всего за одну секунду обучения. Обобщение, достигнутое сетью, стало лучше, но невооружённым взглядом видно, что полученное улучшение несоразмерно затраченным усилиям.
В сердцах, мы покрываем пространство 2048 точками. Вынужденно создаём уже 266 нейронов в ассоциативном слое, подбираем оптимальное количество синапсов на нейрон (получается 
Не знаю, как вы, а я что-то не вижу качественного улучшения. Сеть исправно зазубривает все значения наизусть, ни в малой степени не приближаясь к обобщению предложенной ей закономерности. Да и вообще видно, что характер сделанных сетью глубокомысленных выводов не так уж и сильно зависит от характера стоящей перед ней задачи.
Спасибо, конечно, что сумела хотя бы это выучить. Похоже на то, что теоремы верны, и если я располагаю достаточным количеством нейронов, то смогу заставить сеть заучить хоть все возможные для данной задачи 65536 вариантов, но на это нам потребуется примерно 1500-2000 нейронов и водяное охлаждение. Чтобы запомнить всю информацию, содержащуюся в такой сети, нам потребуется на каждый синапс по 5 бит (4 бита на номер аксона и бит веса), на каждый нейрон 16 бит на значение веса аксона и 40 бит на все синапсы. А один обучающий пример весит 17 бит. В нашем примере с 2048 точками получается, что обучающая информация весит всего в два раза больше, чем информация о полученной сети.
Удобные задачи
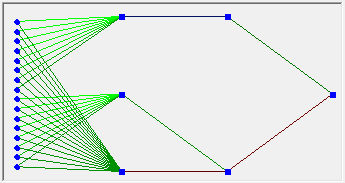
То есть проблема не в том, что перцептрон Розенблатта не может выучиться этому набору данных. Проблема в том, что делать ему это очень и очень неудобно. Кто дружен с теоремой больших чисел, может попробовать прикинуть, какова вероятность встретить подходящее для этого линейно-сепарабельное разложение. Перцептрону Розенблатта удобно решать задачи, хорошо представимые в виде пятнистого сине-зелёного размытого градиента, но всё становится грустно, когда это не так.
А что с многослойным перцептроном Румельхарта?
А что если проблемы только у однослойного перцептрона Розенблатта, а у многосложного перцептрона, обучаемого методом обратного распространения ошибки всё будет очень хорошо, и даже волшебно? Давайте же попробуем.
Исходный код
Во-первых, теперь у нас добавится функция вычисления первой производной от функции активации нейрона при текущих значениях. Всё это можно страшно оптимизировать и синлайнить вычисление производной прямо в формулу, в которой она будет применяться, но наша задача же не в том чтобы всё ускорить, а в том, чтобы разобратся как оно работает. Поэтому отдельная функция:
Производная от функции активации
/// <summary> Функция определения производной от потенциала действия. </summary>
/// <param name="argument">Сумма потенциалов синапсов</param>
/// <param name="funcResult">Потенциал действия нейрона, посчитанный для данных значений</param>
/// <returns>Возвращает значение производной потенциала действия в данной точке.</returns>
public delegate double DTransferFunctionDerivative(double argument, double funcResult);
В качестве сигмоиды воспользуемся, например, Гипертангенсом:
DTransferFunction Function = (x) => Math.Tanh(x),
DTransferFunctionDerivative Derivative = (x, th) => (1 - th) * (1 + th)
Теперь сам нейрон. Он отличается только тем, что при каждом вычислении значения рассчитывает также производную от него по сумме входных сигналов, и наличием переменной, в которой будет храниться значение, используемое для обратного распространения ошибки.
class NeuronWithDerivative
public class NeuronWithDerivative : Neuron {
/// <summary> Производная функции активации нейрона. Она тут хранится отдельно от своего класса чтобы ускорить процесс вызова.</summary>
protected DTransferFunctionDerivative transferFunctionDerivativeDelegate;
/// <summary></summary>
override public DTransferFunctionDerivative TransferFunction {
get { return transferFunctionDerivativeDelegate; }
set { transferFunctionDerivativeDelegate = value; }
}
/// <summary>Хранилище для предвычисленного значения первой производной от функции передачи</summary>
protected double actionPotentialDerivative = 0;
/// <summary>Первая производная от передаточной функции по её основному параметру.</summary>
public double ActionPotentialDerivative { get { return actionPotentialDerivative; } }
/// <summary>Параметр для расчёта обратного распостранения ошибки. Ну, или обратного распостранения производной. Кому как удобнее.</summary>
public double BackProprigationParametr = 0;
public override void Excitation() {
base.Excitation();
actionPotentialDerivative = transferFunctionDerivativeDelegate(synapsPotentials, actionPotential);
}
}
Мне, последнее время, нравится использовать LINQ, потому что так проще и быстрее писать экспериментальный код. Для удобства этого дела моя маленькая домашняя функция, расширяющая его возможности. Использую её вместо List.ForEach чтобы вызов был красивый и однострочный.
static class Tools
static class Tools {
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать.</param>
public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType> func) {
while (source.MoveNext())
func(source.Current);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа и передать ему индекс.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать. Второй параметр передаваемый делегату - индекс в последовательности. Отсчёт начинается со следующего элемента последовательности. В нетронутой - с начала.</param>
public static void Each<SequenceType>(this IEnumerator<SequenceType> source, Action<SequenceType, int> func) {
for (int i = 0; source.MoveNext(); i++)
func(source.Current, i);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать.</param>
public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType> func) {
source.GetEnumerator().Each(func);
}
/// <summary>Вызвать делегата в отношении каждого экземпляра в последовательности любого типа и передать ему индекс.</summary>
/// <param name="source">Перечислитель с исходными данными.</param>
/// <param name="func">Делегат, который надо вызывать. Второй параметр передаваемый делегату - индекс в последовательности. Отсчёт начинается со следующего элемента последовательности. В нетронутой - с начала.</param>
public static void Each<SequenceType>(this IEnumerable<SequenceType> source, Action<SequenceType, int> func) {
source.GetEnumerator().Each(func);
}
}
Сам перцептрон.
class RumelhartPerceptron
// Многослойный перцептрон из обычных сравнительно быстрых нейронов с первой производной.
public class RumelhartPerceptron : NeuralNetwork {
/// <summary> Функция назначаемая нейронам. Задаётся извне.</summary>
DTransferFunctionDerivative TransferFunctionDerivative;
/// <summary>Количество нейронов в сети послойно, не считая сенсорного и выходного слоёв</summary>
public int[] NeuronsCount = new int[0];
override public void create(uint input, uint output) {
// Сенсорные нейроны.
Input = (new SensoryNeuron[input]).Select((empty, index) => new SensoryNeuron(){Name = "S[" + index + "]"}).ToArray();
// Фабрика всех остальных нейронов
Func<string, NeuronWithDerivative> create = (name) => {
NeuronWithDerivative neuron = new NeuronWithDerivative();
neuron.Name = name;
neuron.TransferFunction = TransferFunction;
neuron.TransferFunctionDerivative = TransferFunctionDerivative;
return neuron;
};
Func<IAxon, Synaps> createSynaps = (axon) => { Synaps s = new Synaps(); s.Axon = axon; return s; };
/// <summary>Нейроны внутренних слоёв</summary>
// Составим двумерный массив с нейронами слоёв
NeuronWithDerivative[][] Layers = NeuronsCount.Select((count, layer) => Enumerable.Range(0, count).Select(index => create("A[" + layer + "][" + index + "]")).ToArray()).ToArray();
// Создаём одномерный массив выходных нейронов
// Выходной слой
Output = Enumerable.Range(0, (int)output).Select(index => create("R[" + index + "]")).ToArray();
// Всем нейронам первого слоя навесить связи со слоем сенсоров.
Layers[0].Each(neuron => { Input.Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); });
// Всем нейронам, начиная со второго слоя, связи со всеми нейронами предыдущего слоя.
Layers.Skip(1).Each((layer, layerIndex) => { layer.Each(neuron => { Layers[layerIndex].Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); }); });
// Всем выходным нейронам выдать связи на нейроны
Output.Each(neuron => { Layers.Last().Select(createSynaps).Each(synaps => { neuron.AppendSinaps(synaps); }); });
// Сваливаем всё в очередь выполнения
ExcitationOrder = Layers.SelectMany(layer => layer).Concat(Output).ToArray();
// Рандомизируем веса синапсов в диапазоне от -1 до +1
Random rnd = new Random();
ExcitationOrder.Each(neuron => neuron.Synapses.Each(synaps => synaps.Weight = rnd.NextDouble() * 2 - 1));
}
}
И, наконец, алгоритм обучения. Целиком написан на LINQ потому что так было быстрее написать, и проще редактировать. Да, я знаю, что работает медленнее.
class BackPropagationLearning
public class BackPropagationLearning : LearningAlgorythm {
// Скорость, с которой происходит обучение
public double LearningSpeed = 0.01;
override protected double LearnNet(double[] required) {
double[] errors = net.Output.Select((neuron, index) => neuron.ActionPotential - required[index]).ToArray();
// Почистить все переменные обратного распостранения. Это позволит суммировать обратные переменные, обходя синапсы в порядке их присутствия в нейроне и не создавая двухсвязного списка связей в сети.
net.ExcitationOrder.Cast<NeuronWithDerivative>().Each(neuron => { neuron.BackProprigationParametr = 0; });
// В переменной BackProprigationParametr мы теперь храним dE/dS[i] = dE/dO[i] * F'[i](S[i])
// Для выходных нейронов производная от ошибки зависит от желаемых значений. BP[i] = dE/dO[i] * F'[i] = 2*(O[i]-T[i])*F'[i];
net.Output.Cast<NeuronWithDerivative>().Each((neuron, index) => { neuron.BackProprigationParametr = 2 * errors[index] * neuron.ActionPotentialDerivative; });
// Для всех синапсов посчитать долю производной, которую они внесли в свои аксоны BP[j] = SUM( dE/dO[i] * F'[i] * W[j,i] ) * F'[j] = SUM ( BP[i] * W[j,i] * F'[j])
net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => {
neuron.Synapses.SkipWhile(synaps => !(synaps.Axon is NeuronWithDerivative)).Each(synaps => {
(synaps.Axon as NeuronWithDerivative).BackProprigationParametr += neuron.BackProprigationParametr * neuron.ActionPotentialDerivative * synaps.Weight;
});
});
// А теперь меняем все веса, до которых дотягиваемся delta W[i,j] = -speed * dE/dS[j] * X[i];
net.ExcitationOrder.Reverse().Cast<NeuronWithDerivative>().Each(neuron => {
neuron.Synapses.Each(synaps => {
synaps.Weight += -LearningSpeed * neuron.BackProprigationParametr * synaps.Axon.ActionPotential;
});
});
// И возвращаем средний квадрат ошибки. (Усреднят и возьмут корень из него потом вышестоящие инстанции, для логов).
return errors.Select(e => e * e).Average();
}
public void LearnSomeTime(int sek) {
DateTime begin = DateTime.Now;
while (TimeSpan.FromTicks(DateTime.Now.Ticks - begin.Ticks).Seconds < sek) {
LearnTasksSet();
}
}
}
Вот такой вот код. От самой канонической реализации отличается лишь тем, что скорость обучения не зашита в обратно распространяемую ошибку, а умножается на изменение веса непосредственно перед применением. Минимизируем сумму квадратов ошибок, как учит нас википедия, заполнявшаяся в этой частиами.
Какую задачу подсунем нашей сети для начала? Давайте возьмём те же самые x и y с участка [0,1], В точках, которые выше графика, будем ожидать появления на выходе сети +1, в точках ниже графика -1. Кроме того мы сделаем не одну фиксированную последовательность учебных примеров, а будем создавать новый учебный пример каждый раз заново, чтобы нельзя было сказать, что у сети не было информации о каком-то важном участке пространства. Отдаём созданные пачки переменных по 1000 штук за сет. В превью показывается не одна точка, а несколько последних созданных только для красоты. Получается как-то так.
Создадим нейронную сеть. Википедия нам подсказывает, что трёх слоёв должно быть достаточно. Чтобы не показалось мало, нафигачим по 30 нейронов в слой.Попробуем учить некоторым подобием алгоритма имитации отжига, постепенно вручную уменьшая скорость обучения, по мере того, как среднеквадратичная ошибка за последние 1000 обучающих примеров перестаёт улучшаться. Программировать отжиг было лень, потому что моя статья не про это. Обучаем-обучаем, и наконец, когда качество сети перестают улучшаться рисуем на картинке значения, которые сеть выдаст для каждой из наших точек в квадрате 1×1.
Ну как по мне так довольно скромный результат, а это ещё и лучший из 5 попыток, у него хотя бы есть две вогнутости, это удаётся сети таких размеров не всегда. Обратите внимание на картинку с результатами ещё 4 попыток подряд.
Все попытки дают, в принципе похожий, результат, и на всех картинка завалена влево, не смотря на то, что искомый график во всех этих случая расположен симметрично. Тупость сети можно списать на множество разных причин, включая ошибки в ДНК программиста, но то, что сети удобно заваливаться налево, должно иметь какое-то рациональное объяснение. Так, может быть, мы где-то ошиблись? Давайте предложим сети справиться с совсем уж банальнейшей задачей – дадим в качестве задачи простую линейную зависимость. Смотрим.
Всё хорошо, всё правильно. Отследив вручную состояние переменных можно убедиться, что алгоритм работает правильно. Тогда дадим задачку лишь немного сложнее. Результат можно видеть на следующей картинке.
Полное Фиаско
Вот смотрим мы на это и понимаем, что что-то тут не так. Задача не то, что простая, она примитивная. Но сеть оказывается решительно не способна найти её решение ни в каком приближении.
Вы уже догадались почему? Из картинки явно следует, почему это невозможно, а заодно ответ на вопрос – почему все решения с предыдущей картинки заваливались влево.
Если мы попробуем сконструировать решение данной задачи аналитически – вручную, с ручкой и бумажкой, то очень быстро столкнёмся с правильным ответом. Если у вас в распоряжении нейрон с симметричной сигмоидой никакими ухищрениями вы не заставите его сделать преобразование output = k*input+b. Нейронная сеть с симметричной относительно нуля сигмоидой в точке (0,0) не может выдавать на выходы ничего кроме 0 (привет, кстати, теореме о сходимости перцептрона Розенблатта, там тоже есть такая особенная точка).
Чтобы решить эту проблему мы можем добавить нейронной сети ещё один вход, и выдать ему постоянное значение 1, не зависящее от входных данных. И тут сеть словно бы по мановению волшебной палочки умнеет и обучается стоящей перед ней задаче в кратчайшие сроки и с невероятной доселе точностью.
А может ли существовать неплохое приближение без дополнительного опорного входа? Сможем ли мы придумать решение для топологии сети с предыдущей картинки? Оказывается, это возможно.
Мозг против обратного распостранения
По ходу сети я несколько раз предлагал найти решение для сети вручную. Вот сейчас одно из таких решений мы разберём детально.
Входы сети у нас называются S[0] и S[1], нейроны первого слоя соответственно A[0][1], A[0][2] и A[0][3], следующий слой A[1][0] и A[1][1] и, наконец, выход R[0]. Чего нам не хватало в прошлый раз, когда мы пытались решать задачу аналитически? Нам не хватало опорной константы. Возьмём один нейрон, например A[0][0] и навесим его синапсам очень большие веса, например, по 1000, Кроме маленькой области в непосредственной окрестности 0, потенциал действия на данном нейроне будет равен 1. 
Вот можно посмотреть, как в итоге выглядит сеть:
XML-ка в которую экспортирована готовая сеть
<rumelhart>
<input>
<SensoryNeuron name="S[0]" potential="0,0396039603960396"/>
<SensoryNeuron name="S[1]" potential="0,232673267326733"/>
</input>
<excitationOrder>
<Neuron name="A[0][0]" potential="1">
<synaps weight="999,800400355468" axon="S[0]" potential="39,5960554596225" />
<synaps weight="999,545226476388" axon="S[1]" potential="232,5674536851" />
</Neuron>
<Neuron name="A[0][1]" potential="0,116342019068401">
<synaps weight="1,13712492177543" axon="S[0]" potential="0,0450346503673436" />
<synaps weight="0,308744483692756" axon="S[1]" potential="0,0718365877898986" />
</Neuron>
<Neuron name="A[0][2]" potential="0,29693700450834">
<synaps weight="-0,0240967983057654" axon="S[0]" potential="-0,000954328645772886" />
<synaps weight="1,31992553337836" axon="S[1]" potential="0,307111386479124" />
</Neuron>
<Neuron name="A[1][0]" potential="0,683083451961352">
<synaps weight="1,02404884109051" axon="A[0][0]" potential="1,02404884109051" />
<synaps weight="-0,649771926175146" axon="A[0][1]" potential="-0,0755957778251805" />
<synaps weight="-0,382508459201211" axon="A[0][2]" potential="-0,113580916074308" />
</Neuron>
<Neuron name="A[1][1]" potential="0,0324886810522597">
<synaps weight="-0,404744328902586" axon="A[0][0]" potential="-0,404744328902586" />
<synaps weight="0,161865952018599" axon="A[0][1]" potential="0,0188318116762727" />
<synaps weight="1,40909563283595" axon="A[0][2]" potential="0,418412636280091" />
</Neuron>
</excitationOrder>
<output>
<Neuron name="R[0]" potential="-0,707598983150799">
<synaps weight="-1,36308077548559" axon="A[1][0]" potential="-0,931097921420856" />
<synaps weight="1,50019153981243" axon="A[1][1]" potential="0,0487392444542643" />
</Neuron>
</output>
</rumelhart>
Во всем этом ручном решении есть один интересный момент. Дело в том, что перцептрон, ведомый алгоритмом обратного распространения ошибки, в принципе не мог найти это решение в нашей ситуации. Потому что между начальным состоянием, когда у всех синапсов начальное значение в диапазоне [-1,1] и конечным, при котором два синапса весят очень много, лежит очень широкая пропасть, наполненная очень плохими решениями, и алгоритм градиентного спуска будет старательно выталкивать сеть из этой пропасти. Как я называю это решения имеют высокую несвязанность. Алгоритм имитации отжига может случайно закинуть сеть в ту область, но для этого температура отжига должна быть большой (чтобы был шанс закинуть сеть так далеко) и очень быстро снижаться, чтобы оттуда сразу не выбросило. А ещё поскольку веса части синапсов должны быть большими, а у других, наоборот, очень мало отличаться, мы должны случайно попасть не только в большие значения, но ещё, совершенно случайно, хорошо попасть в маленькие, а ещё алгоритм должен очень резко замерзать когда что-то такое нашёл потому что область годных решений очень узенькая. Даже на скорости обучения 0.0001 простой стохастический градиентный спуск легко может выкинуть из неё сеть. В общем, есть то решение есть, да вот только найти его сеть не может.
Хотя, как вы наверняка заметили, если дать в распоряжение сети три слоя по 30 нейронов, сеть может самостоятельно найти способ частично обрулить проблему нулевой точки. Хотя делать ей это сильно неудобно. Если же мы дадим сети дополнительный опорный вход, картинка перестаёт быть перекошенной на одну сторону. Но и более того сам процесс поиска решения становится гораздо более продуктивным – избавленная от необходимости тратить половину своих бесценных нейронов на создание константы сеть смогла в полную силу развернуться и повести себя так эффективно словно в ней на один слой и ещё несколько десятков нейронов больше. Подробностями можно полюбоваться на картинке.
И решение этой проблемы не единственный способ улучшать качество обучения сети в разы, манипулируя топологией. Я показал именно его просто потому что его можно было красиво продемострировать с аналитическим решением на простейшем примере.
Интересно, что добавление одного входа с константой заметно улучшает работу сети даже в случаях, когда окрестности нулевого значения не попадают во входную задачу, которой мы обучаем сеть. Например ниже я предложил обычной сети, и сети с дополнительным входом одинаковую задачу и одинаково меняющуюся скорость обучения. Причём весь график был сдвинут по обоим осям на единицу, так что на вход сети поступали значения в диапазоне от 1 до 2. Результаты говорят сами за себя.
Наконец если скормить этому алгоритму первую исходную целочисленную задачу, предлагавшуюся перцептрону Розенблатта, результаты будут заметно лучше чем в прошлый раз. Но надо учитывать и то, что в многослойном перцептроне на 30 нейронов синапсов сильно больше, потому, чтобы записать данные сети требуется ощутимо больше байт, чем весят сами исходные денные.
Выводы
- Перцептрон Розенблатта можно научить только таким знаниям, которые в точке с нулевыми входами предполагают нулевой же выход. Если вы интересовались теоремой о сходимости, но не заметили что это из неё следует – значит, перечитайте её более внимательно. Ни за что не поверю, что Розенблатт или Мински могли ошибаться в доказательствах;
- Топология сети влияет на результат заметно больше, чем алгоритм обучения. Если топология делает обучение сети неудобным, скорость обучения падает в разы и даже в десятки раз, а может сделать его попросту невозможным;
- Нейронная сеть легко осваивает только те обобщения, которые легко и удобно сделать на базе её топологии. Все остальные, хоть и возможны в принципе, но или очень маловероятны, или недостижимы из начального состояния сети;
- Обобщение, которое осваивают нейронные сети, в общепринятом в наше время смысле понятие весьма условное. К нему следует относиться со здоровым скептицизмом, если не с иронией;
- То, что задача может быть в принципе решена с помощью нейронной сети, ещё совершенно не значит, что это решение может быть достигнуто из начального состояния сети. Более того связанность пространства решений должна рассматриваться как один из основных факторов при обучении нейронных сетей;
- Добавление на вход простого константного значения во очень многих случаях сильно улучшить качество работы сети для самых разных задач.
Автор: kraidiky
Источник
Искусственный
нейрон
имитирует в первом приближении свойства
биологического нейрона. Он обладает
группой
синапсов
– однонаправленных входных свзей,
соединенных с выходами других нейронов,
а также имеет
аксон
– выходную связь данного нейрона, с
которой сигнал (возбуждения или
торможения) поступает на синапсы
следующих нейронов. Каждый вход
умножается на соответствующий вес,
аналогичный синаптической силе, и все
произведения суммируются, определяя
уровень активации нейрона.
Общий
вид нейрона
на рис. 2.4. Здесь множество входных
сигналов обозначены вектором X. Каждый
вес w, соответствует «силе»
одной биологической синаптической
связи. Множество весов в совокупности
обозначается вектором W.
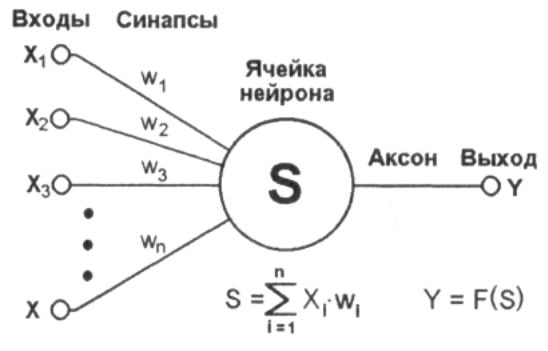
Рис.
2.4. Искусственный нейрон
Нейронная
сеть
является совокупностью элементов,
соединенных
некоторым образом так, чтобы между ними
обеспечивалось взаимодействие.
Эти
элементы,
называемые также нейронами
или
узлами,
представляют
собой простые процессоры, вычислительные
возможности которых обычно ограничиваются
некоторым правилом комбинирования
входных сигналов и правилом
активизации,
позволяющим вычислить выходной сигнал
по совокупности входных сигналов.
Выходной
сигнал элемента
может посылаться другим элементам по
взвешенным связям,
с
каждой из которых связан весовой
коэффициент или
вес.
В
зависимости от значения весового
коэффициента передаваемый сигнал или
усиливается, или подавляется.
Структура
связей
отражает детали конструкции сети, а
именно то, какие элементы соединены, в
каком направлении работают соединения,
и каков уровень значимости (т.е. вес)
каждого из соединений. Задача, которую
понимает сеть (или ее программа),
описывается в терминах весовых значений
связей, связывающих элементы.
Структура
связей обычно определяется в два этапа:
сначала
разработчик системы указывает, какие
элементы должны быть связаны, и в каком
направлении, а затем в процессе фазы
обучения определяются значения
соответствующих весовых коэффициентов.
Весовые
коэффициенты
можно определить и без проведения
обучения, но как раз самое большое
преимущество нейронных сетей заключается
в их способности обучаться выполнению
задачи на основе тех данных, которые
сеть будет получать в процессе реальной
работы.
Существует
множество различных типов
нейронных сетей,
обладающих рядом общих характеристик,
которые можно представить с помощью
следующих абстракций:
• элемент
сети;
• структура
связей;
• правило
распространения сигналов в сети;
• правило
комбинирования входящих сигналов;
• правило
вычисления сигнала активности;
• правило
обучения, корректирующее связи.
Структура
связей
отражает то, как соединены элементы
сети.
В
одной модели
(т.е. для одного типа сетей) каждый
элемент может быть связан со всеми
другими элементами сети,
в
другой модели
элементы могут быть организованы в
некоторой упорядоченной по уровням
(слоям) иерархии, где связи допускаются
только между элементами в смежных
слоях,
а в
третьей
— могут допускаться обратные связи
между смежными слоями или внутри одного
слоя, или же допускаться посылка сигналов
элементами самим себе.
Каждая
связь определяется тремя параметрами:
-элементом,
от которого исходит данная связь,
-элементом,
к которому данная связь направлена,
-и
числом (обычно действительным),
указывающим весовой коэффициент (т.е.
вес связи).
Отрицательное
значение веса соответствует подавлению
активности соответствующего элемента,
а положительное
значение — усилению
его активности. Абсолютное
значение
весового коэффициента характеризует
силу связи.
Вычисление
сигнала активации
Для
всех элементов имеется правило
вычисления выходного значения,
которое предполагается передать другим
элементам или во внешнюю среду (если
речь идет о выходном элементе,
представляющем конечный результат
вычислений). Это правило называют
функцией
активности
(или
функцией
активации),
а
соответствующее выходное значение
называют активностью
соответствующего
элемента.
Активность
может представляться
либо некоторым действительным значением
произвольного вида, либо действительным
значением из некоторого ограниченного
интервала значений (например, из
интервала [0, 1]), или же некоторым значением
из определенного дискретного набора
значений (например, {0, 1} или {+1,-1}).
На
вход функции активности поступает
значение комбинированного ввода данного
элемента.
Активационная
функция может иметь различный вид (рис.
2.9).
В
случае, когда функция активности одна
и та же для всех нейронов сети, сеть
называют однородной
(гомогенной).
Если
же она зависит еще от одного или
не-скольких параметров, значения которых
меняются от нейрона к нейрону, то сеть
называют неоднородной
(гетерогенной).
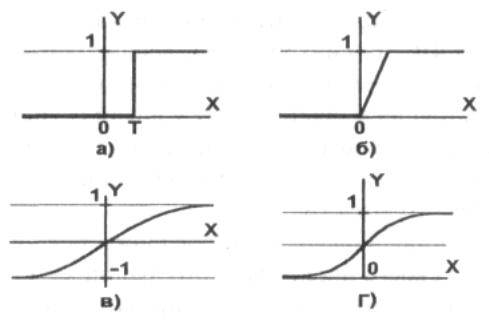
Рис.
2.9. Типы активационных функций:
а –
функция единичного скачка; б – линейный
порог (гистерезис); в – сигмоид –
гиперболический тангенс; г – сигмоид
– формула
Одной
из наиболее распространенных
является нелинейная функция с насыщением,
так называемая логистическая функция
или сигмоид
(т.е. функция
S-образного вида). Она обладает свойством
усиливать слабые сигналы лучше, чем
сильные, и предотвращает насыщение от
сильных сигналов.
Другой
широко используемой
активационной функцией является
гиперболический
тангенс.
В отличие от логистической функции
гиперболический тангенс принимает
значения различных знаков, что для ряда
сетей оказывается выгодным.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #