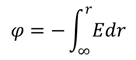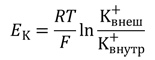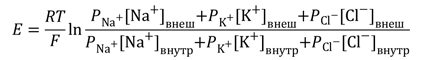The squid giant axon, which is part of a circuit used for rapid propulsion in the escape response, is as large as 1mm in diameter, conducts at 25ms−1 (at 25°C), and is formed by the fusion of axons of many neurons.
From: Encyclopedia of Neuroscience, 2009
Membrane Potential and Action Potential
David A. McCormick, in From Molecules to Networks (Third Edition), 2014
The membrane of the squid giant axon, at rest, is most permeable to K+ ions, less so to Cl−, and least permeable to Na+. (Chloride appears to contribute considerably less to the determination of the resting potential of mammalian neurons.) These results indicate that the resting membrane potential is determined by the resting permeability of the membrane to K+, Na+, and Cl−. In theory, this resting membrane potential may be anywhere between EK (e.g., −76 mV) and ENa (+55 mV). For the three ions at 20 °C, the equation is
Vm=58.2log{(1·20+0.04·440+0.45·40)/(1·400+0.04·50+0.45·560)}=−62mV.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971791000129
Chloride Transporters in Presynaptic Inhibition, Pain and Neurogenic Inflammation
Francisco Javier Alvarez-Leefmans, in Physiology and Pathology of Chloride Transporters and Channels in the Nervous System, 2010
IV. NA+-K+-Cl− Cotransporter Expression in Peripheral Axons and Schwann Cells
The pioneering studies of Russell in squid giant axons demonstrated the expression of an NKCC mechanism in these invertebrate unmyelinated fibers (Russell, 2000). The unique stoichiometry of the cephalopode isoform 2Na+:1 K+:3Cl− suggests differences with respect to vertebrate isoforms which have a stoichiometry of 1Na+:1 K+:2Cl− (see Chapter 5 in this volume). Unfortunately, the squid protein has not been cloned and thus it is not possible to have clues on what makes it different at the molecular level from the vertebrate isoforms. Cloning of the squid NKCC protein would be important to further understanding the evolution of the cation-coupled-chloride cotransport proteins family in the animal kingdom. Moreover, determining the amino acid sequence of squid NKCC would shed light on the molecular determinants of different stoichiometries. The function of NKCC in squid axons appears to be related to cell volume regulation. Russell proposed that “NKCC is an essential component in a feedback mechanism designed to maintain cell volume at some constant set-point”. The evidence presented in the previous section (Figs 22.8 and 22.9) in mammalian DRG neurons is fully consistent with this view.
Work originated in our laboratory provided the first description of NKCC in vertebrate myelinated axons and their associated Schwann cells (Alvarez-Leefmans et al., 2001). We used a combined approach including confocal immunofluorescence, three-dimensional reconstructions and electron microscopy. To label NKCC we used T4 monoclonal antibody (Lytle et al., 1995), and to label Schwann cells we used an antibody against the S-100 protein (Pelc et al., 1986). NKCC immunoreactivity was found prominently at the nodes of Ranvier (Fig. 22.11A–C). Immunoreactivity was particularly intense at the nodal and paranodal regions immediately adjacent to the nodal gap (Fig. 22.11A and C). This particular area corresponds to the so-called myelin sheath attachment segment, according to the nomenclature of Berthold and Rydmark (Berthold and Rydmark, 1983). NKCC immunoreactivity was also systematically observed in the outermost membrane region of the paranodal Schwann cell (arrowheads in Fig. 22.11A). In longitudinal sections of nerve fibers, the NKCC immunoreactivity at the nodal–paranodal area appeared as two bands in the nodal gap, perpendicular to the longitudinal axis of the fiber (arrow in Fig. 22.11A). Upon 40° rotation of three-dimensional confocal reconstructions, the immunoreactivity at the nodal–paranodal region revealed that the bands were actually donut-shaped structures surrounding the axon (Fig. 22.11B, arrow pointing to the node of Ranvier). These donut-shaped regions correspond to the well-known collars of Schwann cell cytoplasm which are known to be packed with Schwann cell microvilli (Fig. 22.11D), reminiscent of the brush border membranes of kidney absorptive epithelial cells (Berthold and Rydmark, 1983).
Figure 22.11. NKCC expression at the nodes of Ranvier in cat myelinated sensory fibers. A. Two-dimensional view of a bundle of myelinated axons. The image was reconstructed from 15 optical sections taken at steps of 1 μm on the z-axis. Intense NKCC immunoreactivity is observed in the paranodal region of the nodes of Ranvier, in the incisures of Schmidt-Lanterman (S-L) and in the outer Schwann cell layer (arrowheads). Immunoreactivity was also found in axons (Ax). B. 40° rotation, showing three-dimensional views of immunoreactive regions. In the 40° rotation, the immunoreactivity in the paranodal region appears as a donut-shaped structure surrounding the axon at the node of Ranvier. These donut-shaped structures correspond to the corona of Schwann cell microvilli observed in electron micrographs (D). Immunoreactive Schmidt-Lanterman incisures appear as funnel-shaped structures. C. Double immunolabeling of NKCC (FITC, green) and S-100 immunolabeling of the Schwann cell (colocalization appears in orange). D. Electron micrograph of a cross-section through a nodal axon segment showing a corona of Schwann cell microvilli. Scale bars in B and C are 20 μm. Scale bar in B applies to A. Scale bar in D = 0.5 μm.
Figures A–C are modified from Alvarez-Leefmans et al. (2001) and reproduced with permission. Figure D was modified from Berthold and Rydmark (1983).
Double labeling experiments with S-100 and T4 confirmed that the NKCC immunoreactivity seen at the nodal–paranodal interface was indeed located at the Schwann cell (Fig. 22.11C). Immunoreactivity was clearly observed in the nodal region, in the area corresponding to the collar-shaped structure surrounding the axon, which is formed by Schwann cell cytoplasmic pockets and microvilli. In fibers cut longitudinally as the one shown in Fig. 22.11C, S-100 immunolabeling revealed that the collar seen in the 3D reconstructions (Fig. 22.11B) appeared as a spiny bracelet structure (Fig. 22.11C, Paranode) similar to that described in classical studies (Landon and Hall, 1976; Nageotte, 1922). Double-labeling studies also confirmed that the myelin sheath was immunonegative but the axon was NKCC immunoreactive (Fig. 22.11A). Electron microscopy revealed that the latter immunoreactivity was located in the axoplasm and in the axolemma (Fig. 22.12B). As the axon passes from the end of the paranodal bulb through the collars formed by the Schwann cell, its diameter is abruptly reduced to about one-third of its internodal value (Fig. 22.11C, green). NKCC immunoreactivity in axons appeared with a punctate pattern and was located both in the axoplasm and in the axolemma region.
Figure 22.12. Ultrastructural distribution of NKCC immunoreactivity in rat myelinated axons. A. Ultrastructural features of the node of Ranvier in a DRG axon. At the node, the axon is loosely covered by microvilli-like cytoplasmic protrusions of the Schwann cell. In the paranodal region, pockets of Schwann cell cytoplasm that arise from the opening of the major dense line surround the axon. Material from Epon-Araldite embedding. B. Myelinated axon in which NKCC-immunoreactive sites appear labeled with 10 nm colloidal gold particles. Intense immunoreactivity is found along the axonal plasma membrane (arrowheads), and to a lesser extent in the Schwann cell and in the axoplasm. Membrane-bound organelles like mitochondria (m) are also surrounded by NKCC immunoreactivity. Unicryl embedding, non-osmicated tissue, T4 mAb 1:1000. C. NKCC immunoreactivity in the node of Ranvier is strongly associated with the paranodal regions (arrows), particularly on the membrane of the Schwann cell paranodal pockets. In the axon, immunoreactivity is found along the axonal plasma membrane, including the nodal axolemma (arrowheads), and throughout the axoplasm. Axoplasmic immunoreactivity appears somewhat concentrated in the nodal region. Unicryl embedding, osmicated tissue, T4 mAb 1:1000. Scale bars 0.5 mm (A, B), 1 mm (C).
Reproduced with permission from Alvarez-Leefmans et al. (2001).
Treating the tissue with the reducing agent β-mercapto-ethanol unmasked NKCC immunoreactivity in the incisures of Schmidt-Lanterman (S-L in Fig. 22.11B–C). The latter are inclusions of Schwann cytoplasm within the myelin which pursue a spiral course across the sheath, forming cylindrico-conical segments at the internodes, and so connecting the external and internal layers of Schwann cell cytoplasm (Ghabriel and Allt, 1981; Landon and Hall, 1976), as illustrated in the unrolled Schwann cell in Fig. 22.13A. In 3D rotations, the funnel shape of the NKCC-immunoreactive incisures of Schmidt-Lanterman could be more clearly appreciated (Fig. 22.11B). The longitudinally sectioned Schmidt-Lanterman incisures can also be appreciated in the S-100 and T4 double immunolabeling (Fig. 22.11C).
Figure 22.13. Diagrams showing NKCC location in various elements of a myelinated sensory fiber and the possible functional significance of NKCC in axons and Schwann cells. A. Unrolling of the Schwann cell sheath from an axon. The white areas indicate the presence of Schwann cell cytoplasm. The areas with black points indicate compact myelin. The unrolled sheath shows the transverse and longitudinal Schmidt-Lanterman incisures. Note the nucleus of the Schwann cell in the outer cytoplasmic belt, the microvilli and the terminal cytoplasmic spiral. NKCC immunoreactivity is indicated in red for the Schwann cell and in green for the axon. B. When rolled back around the axon, the terminal cytoplasmic spiral runs around the paranodal attachment segment many times, creating Schwann cell pockets or paranodal loops that, together with microvilli, overhang the paranodal and nodal axon, respectively. When transversally cut, this nodal–paranodal bracelet forms collars surrounding the axon, like the ones shown in Fig. 22.11B and D. C. Functional significance of NKCC in axons and Schwann cells. We propose that NKCC located in the Schwann cell may be involved in periaxonal K+ homeostasis. External K+ ion accumulation occurs in the paranodal areas of the Schwann cell, in particular during repetitive firing. During each action potential, Na+ enters the axon through voltage-gated channels located in the nodal area, and K+ exits the axon via voltage-gated channels located in the nodal–paranodal interface. The preferential location of NKCC in the paranodal areas of the Schwann cell suggests that it could be involved in the uptake of K+ released from the axon and then in siphoning it to areas far away from the periaxonal space, thereby preventing periaxonal K+ accumulation and controlling axonal excitability. Uptake of K+ by the Schwann cell can also occur through inward rectifier K+ channels (IR). The release of K+ taken up by the Schwann cell may occur through delayed rectifier channels (DR) located in the outer membrane, opposite to the periaxonal space. “Tight junctions” (TJ) restrict access to the extracellular spaces within the myelin, and “transverse junctions” (TB) maintain a narrow periaxonal space in the paranodal region. NKCC in axons may be involved in cell volume control and intracellular Cl− regulation and, in conjunction with the Na+/K+ pump, in the reuptake of K+ released during nerve activity.
A and B are reproduced with permission from Alvarez-Leefmans et al. (2001).
The distribution of immunoreactivity in rat myelinated axons was studied ultrastructurally and was found to be very similar to that observed using confocal microscopy in cat myelinated axons (Fig. 22.12). Membrane immunostaining was detected in Schwann cell paranodal pockets and microvilli, and along the axonal membrane at the nodal and paranodal regions (Fig. 22.12B–C). NKCC was found in both the axoplasm and in the membrane region of axons, as well as in three well-defined regions of the Schwann cell: the external surface along the internodal segment (paranode), the nodal–paranodal region (myelin sheath attachment segment) and the incisures of Schmidt-Lanterman. These findings are summarized in Fig. 22.13A and B. The location of NKCC in these structures suggests that it may be playing a role in periaxonal K+ homeostasis. Frankenhaeuser and Hodgkin first suggested that K+ released by axons during activity could be transiently accumulated in the periaxonal space between Schwann cells and axons (Frankenhaeuser and Hodgkin, 1956). Since extracellular K+ has a profound influence on excitability, efficient K+ clearance is critical for nerve function.
It has been suggested that periaxonal K+ is partly regulated by the Schwann cells. Two mechanisms have been proposed: inwardly rectifying K+ channels (Chiu, 1991, 1995) and the Na+/K+ pump (Ransom et al., 2000), both of which are present in the plasma membrane of Schwann cells (Fig. 22.13C). We proposed that NKCC exhibits the kinetic features required for an efficient extracellular K+ buffer, as discussed also in Chapter 5. The immunolocalization of NKCC suggests that NKCC may be another major mechanism involved in periaxonal K+ buffering in peripheral myelinated axons (Fig. 22.13C).
Modeling activity-dependent K+ accumulation in various compartments of mammalian myelinated fibers, Chiu showed that the largest extracellular K+ accumulation is expected to occur at the adjacent 2–4 μm length of periaxonal space at the nodal–paranodal interface (Chiu, 1991), the region in which NKCC is highly concentrated (Figs 22.11B–D and 22.14). Indeed, this is the region where Schwann cell microvilli prominently express NKCC. These microvilli represent a dramatic increase in the ratio of surface area to volume seen in typical absorptive epithelia (Fig. 22.11D). The total membrane area of the microvilli is about ten to 15 times that of the nodal area (Berthold and Rydmark, 1983). Activity-dependent paranodal K+ accumulation of the magnitude predicted by the model (Fig. 22.14E) may cause sufficient depolarization to compromise repetitive conduction of impulses. In the paranodal region, diffusion alone is not sufficient to avoid K+ accumulation, as is the case for the nodal region. The features of the paranodal Schwann cell are well designed to act as a powerful periaxonal K+ buffering system. Experiments to test this hypothesis, using electrophysiological methods, are much needed.
Figure 22.14. Computer simulation of K+ accumulation in the nodal and paranodal periaxonal compartments of a myelinated fiber during non-propagating action potentials, assuming that the only K+ clearance mechanism is diffusion. A. Equivalent circuit used in the simulation. Values used in the model are described in Chiu (1991). B. and C. Ionic currents during a single non-propogating action potential in the nodal region (A) and in the paranodal region (B). D. and E. Activity-dependent accumulation of K+ in the nodel gap (D) and in the periaxonal space between the paranodal axon and the paranodal myelin (E). Note the different scales for [K+]o between D and E. If there were no K+ clearance mechanisms other than difussion, the periaxonal K+ accumulation would be two orders of magnitude higher in the paranode (10 mM), depolarizing the node and compromising action potential conduction.
(Modified from Chiu, 1995; reproduced with permission from Oxford University Press.)
Finally, the presence of NKCC in the axonal membrane deserves further comment. As already mentioned, at the time in which our work was published (2001), NKCC had only been reported in unmyelinated squid axons, as already mentioned (Russell, 2000). The presence of NKCC in mammalian peripheral axons and terminals (see below) suggests that the protein is transported from the cell bodies to distal regions of sensory neurons. Further, the fact that GABA depolarizes sensory axons, including myelinated or unmyelinated (see above, section II.A), suggests that the NKCC protein is also functional as an active Cl− uptake system, maintaining an outward Cl− gradient over the entire length of axon. NKCC in peripheral sensory axons may be involved in reuptake of K+ following nerve activity, as well as in cell volume control. The functional meaning of depolarizing GABAA extrajunctional receptors in sensory axons is still unknown. GABA in the periphery might play a role in the control of excitability and action potential propagation (Verdier et al., 2003). Interestingly, expression of NKCC1 in vagal sensory endings innervating the airways has been demonstrated (Mazzone and McGovern, 2006). Depolarzing Cl− currents determine nerve ending activation underlying cough reflexes. In central neurons, GABA mediates a depolarizing response at the axon initial segments of cortical pyramidal cells (Szabadics et al., 2006). As in peripheral axons, the outward Cl− gradient is caused by NKCC1 (Khirug et al., 2008). The functional meaning of these interactions in cortical neurons is intriguing, and remains to be elucidated.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123743732000224
Methods and Models in Neurophysics
C. Pouzat, in Les Houches, 2005
3.2.1. An experimental illustration from projection neurons in the locust antennal lobe
It is well known and understood since the squid giant axon study by Hodgkin and Huxley that once a neuron (or a piece of it like its axon) has fired an action potential, we must wait “a while” before the next action potential can be fired. This delay is dubbed the refractory period and is mainly due to inactivation of sodium channels and to strong activation of potassium channels at the end of the spike, meaning that we must wait for the potassium channels to de – activate and for sodium channel to de – inactivate. Phenomenologically it means that we should observe on the inter – spike interval (ISI) histogram from a single neuron a period without spikes (i.e., the ISI histogram should start at zero and stay at zero for a finite time). In addition we can often find on ISI histograms some other features like a single mode2
a “fast” rise and a “slower” decay as illustrated on Fig 4. The knowledge of the ISI histogram can in principle be used to improve spike – sorting because it will induce correlations between the labeling of successive spikes. Indeed, if in one way or another we can be sure of the labeling of a given spike to a given neuron, we can be sure as well that the probability to have an other spike from the same neuron within say the next 10 ms is zero, that this probability is high between 30 and 50 ms and high as well between 60 and 100 (you just need to integrate the ISI histogram to see that).
Fig. 4.. An example of ISI pdf estimates for 8 projection neurons simultaneously recorded in the locust antennal lobe (Pouzat, Mazor and Laurent, unpublished).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0924809905800216
Computational Neuroscience
Bertil Hille, … Bjoern Falkenburger, in Progress in Molecular Biology and Translational Science, 2014
3.1 General considerations
In their classical study of ion channels of the squid giant axon, Hodgkin and Huxley1 looked at a distal event (ionic current) and presumed internal, “hidden” gating states to best fit their data. They did not assume that their four “gating particles” had a molecular substrate, but when, decades later, ion channels were found to indeed contain four voltage sensors, their work appeared almost prophetic. We believe that two factors were instrumental for their successful predictions. One is their aim to simulate not a single-current trace, but currents over wide ranges of voltages, pulse durations, and ion concentrations. The second is that currents of giant axons are readily measured with high accuracy and good signal-to-noise ratio. This allows accurate fitting of activation and deactivation kinetics at many voltages.
Similarly, in our modeling of the G-protein-coupled cascade, we used measurements of kinetics over a wide range of agonist concentrations to probe the system we study. However, this system is different. We did not have to assume “hidden” states because much is known about the intermediate molecules of G-protein-coupled signaling. Our aim was not to “best fit the data,” but to incorporate known intermediate states that represent actual measurable molecular steps of the signaling cascade. We wanted to see how all the known steps worked together to produce the macroscopic channel modulation.
Another difference from the situation of Hodgkin and Huxley is that responses of small cells are more variable than those of giant axons. Hence, individual recordings are less reproducible and dose–response curves more “noisy.” Further, many of the optical measurements we use have lower signal-to-noise ratio than whole-cell current. Taken together, these factors make it more difficult to tweak intermediate steps by fitting the exact shape of a downstream curve.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123978974000085
Controversies In Diabetic Neuropathy
S.M. Emery, R.T. Dobrowsky, in International Review of Neurobiology, 2016
3.1 Import, Export, and Neuronal Support
Hsp70 export was unknowingly first characterized in heat-treated giant squid axon when protein levels of a heat shock-like transferrin protein increased in the axoplasm (Tytell et al., 1986). This transferrin protein was specifically identified as Hsp70 when heat-treated rat embryonic cell cultures (presumably fibroblasts) were shown to release Hsp70 into the media, independent of an increase in cell death (Hightower & Guidon, 1989). Glial eHsp70 secretion has also been confirmed in models of heat-treated glioblastoma cells (Guzhova et al., 2001).
The export mechanisms behind eHsp70 secretion are still not well understood since Hsp70 lacks a secretory signal sequence and inhibiting the secretory pathway has no effect on the release of eHsp70 (Hightower & Guidon, 1989). Some evidence has pointed toward an innate ability of the protein to traverse the cell membrane (Multhoff, 2007), lipid raft-mediated lysosomal release (Hunter-Lavin et al., 2004), and secretory-like granule excretion (Evdonin et al., 2006). However, the largest collection of evidence points to exosome-dependent trafficking; heat-shocked peripheral blood mononuclear cells increased eHsp70 levels and produced Hsp70-loaded exosomes (Lancaster & Febbraio, 2005). Though further study is needed to fully understand this Hsp70 export mechanism, exosomal eHsp70 release has been demonstrated in other models including colon and pancreatic cancer cell lines (Gastpar et al., 2005) as well as breast and leukemic cancer cells (Bausero, Gastpar, Multhoff, & Asea, 2005).
Once excreted eHsp70 can be absorbed and utilized by neighboring cells, typically for the purpose of cell support (Guzhova et al., 2001). The neuroblastoma cell line LAN-5 showed lower levels of cytotoxicity from both heat shock and staurosporine treatment after internalizing exogenously administered Hsp70 (Guzhova et al., 2001). These cytoprotective effects can likewise translate to nonneoplastic neuronal models. Injection of recombinant human Hsp70 into G93A mutant Cu/Zn superoxide dismutase (SOD1) mice helped preserve motor neurons resulting in a delayed onset of amyotrophic lateral sclerosis (ALS) symptoms (Gifondorwa et al., 2007). In vitro and ex vivo experiments using a trophic factor-deprived environment and sciatic nerve axotomy, respectively, confirm eHsp70 decreased motor neuron death (Robinson et al., 2005; Tidwell, Houenou, & Tytell, 2004). Exogenously administered Hsp70 also preserved viability of dorsal root ganglia (DRG) sensory neurons after sciatic nerve axotomy (Tidwell et al., 2004). Though the exact mechanism for cellular protection is not known, eHsp70 may act as iHsp70 upon internalization (Turturici, Sconzo, & Geraci, 2011).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/S0074774216300216
Batrachotoxin☆
M. Cataldi, in Reference Module in Biomedical Sciences, 2016
Pharmacological Effects
Neuromuscular: Effect on nerve conduction: Studies performed on squid giant axons revealed that BTX induces membrane depolarization and causes a progressive decrease in the amplitude of action potentials elicited by the electrical stimulation of the fiber (Albuquerque et al., 1971a,b; Albuquerque et al., 1973; Narahashi et al., 1971a,b).
BTX blocks axonal transport and induces axonal necrosis in a Na+ dependent manner (Boegman and Riopelle, 1980; Boegman et al., 1980; Deshpande et al., 1981; Hudson et al., 1984; Moore et al., 1981; Worth and Ochs, 1982). A subarachnoid injection of BTX into the spinal cord causes paraplegia in rats paraplegic due myelopathic damage (Boegman and Albuquerque, 1980; Garcia et al., 1978).
Effects on neurotransmitter release: In vivo studies indicate that BTX induces a massive release of 5-HT from the caudate nucleus (Hery et al., 1979) and from the raphe nuclei in cat (Hery et al., 1982), and VIP release from brain slices (Besson et al., 1982). It has been suggested that BTX causes massive neuronal activation based on the fact that it increases cAMP synthesis (Shimizu et al., 1970a,b) and phosphoinositide turnover (Benuck et al., 1989) in brain slices. BTX increases the affinity for carbachol and acetylcholine of muscarinic acetylcholine receptors in brainstem and ventricle, but not in the cerebral cortex. Because this effect disappeared in the presence of tetrodotoxin it was suggested that muscarinic receptors directly interact with NaV channels (Cohen-Armon et al., 1985). Kayaalp et al. (1970) demonstrated that BTX causes a prolonged blockade of sympathetic ganglionic transmission by blocking impulse conduction in the preganglionic sympathetic nerve fiber.
Effects on neuromuscular transmission: BTX makes muscle fibers unexcitable while promoting the appearance of muscle contractures. In the presence of the toxin there is an irreversible block of indirectly and directly elicited muscle twitch (Warnick et al., 1971). The earliest electrophysiological effect is a significant increase in the frequency of miniature end-plate potentials caused by an increase in presynaptic neurotransmitter release that results from an increase in Na+ influx into presynaptic terminals (Jansson et al., 1974). The increase in presynaptic Na+ concentration causes a progressive depolarization in nerve terminals leading to a progressive decrease in action potential amplitude. When action potential amplitude decreases to a half of the starting values, evoked transmitter release is abolished as is the muscle response to the electrical stimulation of nerve afferents (Jansson et al., 1974).
Effects on muscle: BTX and its analogues cause early and late muscle contractures. The early contractures appear during the first minutes after toxin administration and depend on the direct effect of the toxin on muscle membranes rather than to an effect on Ach release (Warnick et al., 1971). Late muscle contractures appear 20 min or more after toxin administration and are probably dependent on Ca2 + release from intracellular stores (Albuquerque et al., 1971b; Warnick et al., 1971).
BTX induces degenerative changes in muscle ultrastructure including swelling and destruction of terminal cisternae and of the longitudinal part of the sarcoplasmic reticulum (Albuquerque et al., 1971b). Ultrastructural changes are observed in the motor endplate as well, including swelling of nerve terminals and deformation and darkening of synaptic vescicles.
Cardiovascular effects: BTX causes atrioventricular block and a wide array of ventricular arrhythmias eventually leading to ventricular fibrillation and death. Microelectrode recordings in Purkinje fibers revealed an increase in the duration of the action potential and the appearance of afterpotentials early after BTX exposure, well before the membrane becomes persistently depolarized. Cardiac cells become unexcitable when the plasma membrane potential settles at values around − 20 mV (Hogan and Albuquerque, 1971).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780128012383993796
The voltage-gated channels of Na+ action potentials
Constance Hammond, in Cellular and Molecular Neurophysiology (Fourth Edition), 2015
Abstract
The ionic basis for nerve excitation was first elucidated in the squid giant axon by Hodgkin and Huxley (1952) using the voltage clamp technique. They made the key observation that two separate voltage-dependent currents underlie the action potential: an early transient inward Na+ current which depolarizes the membrane, and a delayed outward K+ current largely responsible for repolarization. This led to a series of experiments that resulted in a quantitative description of impulse generation and propagation in the squid axon. Nearly 30 years later, Sakmann and Neher, using the patch clamp technique, recorded the activity of the voltage-gated Na+ and K+ channels responsible for action potential initiation and propagation. Taking history backwards, action potentials will be explained from the single channel level to the membrane level.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123970329000042
Na+-Ca2+ Exchange Currents
John H.B. Bridge, … Michela Ottolia, in Cell Physiology Source Book (Fourth Edition), 2012
VIIC Phosphorylation
It has been known for some time that exchange activity in squid giant axons could be regulated by ATP. The main effect of ATP is to increase the affinity of the exchanger for its substrates Na+ and Ca2+. Moreover, recent evidence suggests the involvement of a Ca2+-dependent protein kinase. It appears that, at least in the squid, Na+-Ca2+ exchange that is stimulated by ATP requires intracellular Ca2+ and can be mimicked by hydrolyzable ATP analogs (DiPolo and Beauge, 1987a,b).
It has been difficult to demonstrate regulatory effects of ATP in cardiac tissues. The whole-cell isolated patch technique does not lend itself to studies of this nature because it is extremely difficult, if not impossible, to control intracellular ATP concentrations. However, recent evidence suggests that the molecule may be phosphorylated and regulated by two mechanisms. One which remains controversial is that phophorylation can take place by β-adrenergic/PKA activation. There appears to be stronger evidence that PKC mediated signaling can regulate NCX phosphorylation. We refer the interested reader to the review by Zhang and Hancox (Zhang and Hancox, 2009).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123877383000147
Dynamical Properties of Excitable Membranes
Douglas A. Baxter, John H. Byrne, in From Molecules to Networks (Third Edition), 2014
Hodgkin and Huxley conducted their voltage-clamp experiments on the squid giant axon at the Marine Biological Laboratory in Plymouth, England. Although the Plymouth laboratory was badly damaged during the great air raids of 1941, it was partially rebuilt by the time Hodgkin and Huxley arrived in July of 1949. With the help of Bernard Katz and their improved voltage-clamp apparatus, it took them only a month to obtain all of the voltage-clamp records that were used in the five papers published in 1952 (Hodgkin et al., 1952; Hodgkin and Huxley, 1952a−d). Upon returning to the University of Cambridge, they spent the next two years analyzing the data and preparing the manuscripts. By March 1951, they had settled on a set of the equations and parameters that adequately described the time course, magnitude and voltage dependency of the membrane currents that were observed during voltage-clamp steps. It was by no means a foregone conclusion, however, that these same equations would describe the behavior of the membrane under its normal operating conditions. Thus, the final stage of their analysis was to calculate the response of their mathematical representation of the nerve to the equivalent of an electrical stimulus. If the calculations produced an action potential that agreed favorably with experimental data, this would help validate their model.
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B9780123971791000142
Principles
Toshio Narahashi, in Handbook of Pesticide Toxicology (Second Edition), 2001
Amplification of Pyrethroid Toxicity from Sodium Channels to Animals
An early study by Lund and Narahashi (1982) using squid giant axons suggested that only a very small fraction of the sodium channel population needed to be modified by pyrethroids to cause repetitive discharges. This was based on the calculation of the percentage of sodium channels needed to increase the depolarizing after-potential to the level of threshold membrane potential for generation of repetitive action potentials. However, a few assumptions had to be made for calculation, as not all data were available at that time. Later, Tatebayashi and Narahashi (1994) developed a method to calculate the percentage of sodium channel modification caused by pyrethroid based on patch clamp data using rat DRG neurons. Since the peak sodium current (INa) during a depolarizing pulse was not affected by pyrethroid, it represented the activity of normal or unmodified sodium channels. The tail current (Itail) upon termination of a depolarizing pulse appeared only after application of pyrethroid, and therefore it represented the activity of modified sodium channels. The percentage of modification (M) can be calculated by the following equation:
(1)M=[{Itail/(Eh−ENa)}/{INa/(Et−ENa)}]×100
where Itail is the tail current amplitude obtained by extrapolation of the slowly decaying phase of the tail current to the moment of membrane repolarization assuming a single exponential decay, Eh is the potential to which the membrane was repolarized, ENa is the equilibrium potential for sodium ions obtained as the reversal potential for sodium current, and Et is the potential of step depolarization. The percentages of sodium channels modified by tetramethrin were very small: for example, for TTX-S sodium channels, 0.24%, 3.53%, and 12.03% by 0.1,1, and 10 μM tetramethrin, respectively; for TTX-R sodium channels, 1.31%, 15.35%, 57.82%, and 81.20% by 0.01, 0.1, 1, and 10 μM tetramethrin, respectively. Thus, TTX-R sodium channels are approximately 30 times more sensitive to tetramethrin than TTX-S sodium channels.
A question arises as to the degree of pyrethroid modification needed to cause repetitive nerve activity. Using the same method of calculation and also comparing these calculated data with the threshold concentration for tetramethrin needed to induce repetitive discharges in rat cerebellar Purkinje neurons, an astonishingly small percentage was obtained, that is, 0.62%, as illustrated in Fig. 12.4 (Song and Narahashi, 1996). This provides one of the bases for high potency of pyrethroid action. It is also important to note that the significance of this “toxicity amplification” is not limited to pyrethroids. When a drug slightly suppresses the slow depolarization (e.g., caused by activation of T-type calcium channels or in epileptic seizure), repetitive discharges generated by the slow depolarization will stop, and for this action only a concentration of the drug (e.g., antiepileptic drug) much lower than the IC50 for suppressing the depolarization (or calcium channels) will be needed, perhaps IC10 or even IC1. Thus, “pharmacological amplification” will become important for interpreting the drug action in vivo. The traditional concept of relating in vitro IC50 to a patient’s serum concentration of the drug may not necessarily be valid when the effect is exerted via the threshold phenomenon.
Figure 12.4. Concentration-dependent effect of tetramethrin on TTX-S sodium currents of rat cerebellar Purkinje neurons. (a) Currents were evoked by a 5-msec step depolarization to 0 mV from a holding potential of −110 mV under control conditions and in the presence of tetramethrin (0.3 μM, 3 μM, and 10 μM). TTX (0.5 μM) completely blocked both the peak current and the tetramethrin-induced tail current. (b) The concentration-response relationship for induction of tail current. Each point indicates the mean ± S.E.M. (n = 6). Data were fitted by the Hill equation. The percentages of channels modified by tetramethrin are 0.62 ± 0.15%, 2.19 ± 0.36%, 5.75 ± 0.87%, 13.58 ± 1.35%, 22.77 ± 2.26%, and 24.73 ± 2.11% at concentrations of 0.1, 0.3, 1, 3, 10, and 30 μM, respectively (n = 6). (c) Repetitive after-discharges caused by 100 nM tetramethrin, the threshold concentration. Action potentials were evoked by applying a current pulse (2 msec, 200 pA). Em refers to the membrane potential. From Song and Narahashi (1996).
Read full chapter
URL:
https://www.sciencedirect.com/science/article/pii/B978012426260750015X
Статья на конкурс «био/мол/текст»: Потенциал покоя — это важное явление в жизни всех клеток организма, и важно знать, как он формируется. Однако это сложный динамический процесс, трудный для восприятия целиком, особенно для студентов младших курсов (биологических, медицинских и психологических специальностей) и неподготовленных читателей. Впрочем, при рассмотрении по пунктам, вполне возможно понять его основные детали и этапы. В работе вводится понятие потенциала покоя и выделяются основные этапы его формирования с использованием образных метафор, помогающих понять и запомнить молекулярные механизмы формирования потенциала покоя.
«Био/мол/текст»-2011
Эта статья представлена на конкурс научно-популярных работ «био/мол/текст»-2011 в номинации «Лучшая обзорная статья».
Мембранные транспортные структуры — натрий-калиевые насосы — создают предпосылки для возникновения потенциала покоя. Предпосылки эти — разность в концентрации ионов на внутренней и наружной сторонах клеточной мембраны. Отдельно проявляет себя разность концентрации по натрию и разность концентрации по калию. Попытка ионов калия (K+) выровнять свою концентрацию по обе стороны мембраны приводит к его утечке из клетки и потере вместе с ними положительных электрических зарядов, за счёт чего значительно усиливается общий отрицательный заряд внутренней поверхности клетки. Эта «калиевая» отрицательность составляет бóльшую часть потенциала покоя (−60 мВ в среднем), а меньшую его часть (−10 мВ) составляет «обменная» отрицательность, вызванная электрогенностью самого ионного насоса-обменника.
Давайте разбираться подробнее.
Зачем нам нужно знать, что такое потенциал покоя и как он возникает?
Вы знаете, что такое «животное электричество»? Откуда в организме берутся «биотоки»? Как живая клетка, находящаяся в водной среде, может превратиться в «электрическую батарейку» и почему она моментально не разряжается?
Совершенно очевидно, что для понимания того, как работает нервная система, необходимо вначале разобраться, как работает её отдельная нервная клетка — нейрон. Главное, что лежит в основе работы нейрона — это перемещение электрических зарядов через его мембрану и появление вследствие этого на мембране электрических потенциалов. Можно сказать, что нейрон, готовясь к своей нервной работе, вначале запасает энергию в электрической форме, а затем использует ее в процессе проведения и передачи нервного возбуждения.
Таким образом, наш самый первый шаг к изучению работы нервной системы — это понять, каким образом появляется электрический потенциал на мембране нервных клеток. Этим мы и займёмся, и назовём этот процесс формированием потенциала покоя.
Определение понятия «потенциал покоя»
В норме, когда нервная клетка находится в физиологическом покое и готова к работе, у неё уже произошло перераспределение электрических зарядов между внутренней и наружной сторонами мембраны. За счёт этого возникло электрическое поле, и на мембране появился электрический потенциал — мембранный потенциал покоя.
Как известно из физики, электрические заряды (движущиеся и неподвижные) формируют в пространстве электромагнитное поле, которое влияет на тела, обладающие электрическим зарядом. С точки зрения электромагнетизма клеточную мембрану можно представить как плоский конденсатор, заполненный однородным диэлектриком из неполярных молекул. Если конденсатор заряжен, то внутри него возникает электрическое поле, обусловленное поверхностной плотностью заряда. На поверхности мембраны возникают некомпенсированные заряды: положительные у «отрицательной» поверхности и отрицательные — у «положительной» [6].
Таким образом, мембрана оказывается поляризованной. Это означает, что она имеет разный электрический потенциал наружной и внутренней поверхностей. Разность между этими потенциалами вполне возможно зарегистрировать.
В этом можно убедиться, если ввести внутрь клетки микроэлектрод, соединённый с регистрирующей установкой. Как только электрод попадает внутрь клетки, он мгновенно приобретает некоторый постоянный электроотрицательный потенциал по отношению к электроду, расположенному в окружающей клетку жидкости. Величина внутриклеточного электрического потенциала у нервных клеток и волокон, например, гигантских нервных волокон кальмара, в покое составляет около −70 мВ. Эту величину называют мембранным потенциалом покоя (МПП). Во всех точках аксоплазмы этот потенциал практически одинаков.
Ещё немного физики. Макроскопические физические тела, как правило, электрически нейтральны, т.е. в них в равных количествах содержатся как положительные, так и отрицательные заряды. Зарядить тело можно, создав в нем избыток заряженных частиц одного вида, например, трением о другое тело, в котором при этом образуется избыток зарядов противоположного вида. Учитывая наличие элементарного заряда (e), полный электрический заряд любого тела можно представить как q = ±N×e, где N — целое число.
Потенциал электростатического поля φ определяется как отношение потенциальной энергии W пробного заряда q к величине этого заряда: φ = W/q, откуда следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Единицей измерения потенциала служит вольт (1 В) [4]. В некоторых случаях потенциал электрического поля нагляднее определяется как физическая величина, численно равная работе внешних сил против сил электрического поля E при перемещении единичного положительного точечного заряда из бесконечности в данную точку. Последнее определение удобно записать следующим образом:
В электрофизиологии кроме потенциала покоя рассматриваются и другие электрические потенциалы: локальные постсинаптические и рецепторные потенциалы (возбуждающие и тормозные), электротонические и следовые потенциалы, миниатюрные потенциалы концевой пластинки, концентрационный потенциал и потенциал действия [5].
Потенциал покоя — это разность электрических потенциалов, имеющихся на внутренней и наружной сторонах мембраны, когда клетка находится в состоянии физиологического покоя. Его величина измеряется изнутри клетки, она отрицательна и составляет в среднем −70 мВ (милливольт), хотя в разных клетках может быть различной: от −35 мВ до −90 мВ.
Важно учитывать, что в нервной системе электрические заряды представлены не электронами, как в обычных металлических проводах, а ионами — химическими частицами, имеющими электрический заряд. И вообще в водных растворах в виде электрического тока перемещаются не электроны, а ионы. Поэтому все электрические токи в клетках и окружающей их среде — это ионные токи.
Итак, изнутри клетка в покое заряжена отрицательно, а снаружи — положительно. Это свойственно всем живым клеткам, за исключением, разве что, эритроцитов, которые, наоборот, заряжены отрицательно снаружи. Если говорить конкретнее, то получается, что снаружи вокруг клетки будут преобладать положительные ионы (катионы Na+ и K+), а внутри — отрицательные ионы (анионы органических кислот, не способные свободно перемещаться через мембрану, как Na+ и K+).
Теперь нам всего лишь осталось объяснить, каким же образом всё получилось именно так. Хотя, конечно, неприятно сознавать, что все наши клетки кроме эритроцитов только снаружи выглядят положительными, а внутри они — отрицательные.
Термин «отрицательность», который мы будем применять для характеристики электрического потенциала внутри клетки, пригодится нам для простоты объяснения изменений уровня потенциала покоя. В этом термине ценно то, что интуитивно понятно следующее: чем больше отрицательность внутри клетки — тем ниже в отрицательную сторону от нуля смещён потенциал, а чем меньше отрицательность — тем ближе отрицательный потенциал к нулю. Это намного проще понять, чем каждый раз разбираться в том, что же именно означает выражение «потенциал возрастает» — возрастание по абсолютному значению (или «по модулю») будет означать смещение потенциала покоя вниз от нуля, а просто «возрастание» — смещение потенциала вверх к нулю. Термин «отрицательность» не создаёт подобных проблем неоднозначности понимания.
Сущность формирования потенциала покоя
Попробуем разобраться, откуда берётся электрический заряд нервных клеток, хотя их никто не трёт, как это делают физики в своих опытах с электрическими зарядами.
Здесь исследователя и студента поджидает одна из логических ловушек: внутренняя отрицательность клетки возникает не из-за появления лишних отрицательных частиц (анионов), а, наоборот, из-за потери некоторого количества положительных частиц (катионов)!
Так куда же деваются из клетки положительно заряженные частицы? Напомню, что это покинувшие клетку и скопившиеся снаружи ионы натрия — Na+ — и калия — K+.
Главный секрет появления отрицательности внутри клетки
Сразу откроем этот секрет и скажем, что клетка лишается части своих положительных частиц и заряжается отрицательно за счёт двух процессов:
- вначале она обменивает «свой» натрий на «чужой» калий (да-да, одни положительные ионы на другие, такие же положительные);
- потом из неё происходит утечка этих «наменянных» положительных ионов калия, вместе с которыми из клетки утекают положительные заряды.
Эти два процесса нам и надо объяснить.
Первый этап создания внутренней отрицательности: обмен Na+ на K+
В мембране нервной клетки постоянно работают белковые насосы-обменники (аденозинтрифосфатазы, или Na+/K+-АТФазы), встроенные в мембрану. Они меняют «собственный» натрий клетки на наружный «чужой» калий.
Но ведь при обмене одного положительного заряда (Na+) на другой такой же положительный заряд (K+) никакого дефицита положительных зарядов в клетке возникать не может! Правильно. Но, тем не менее, из-за этого обмена в клетке остаётся очень мало ионов натрия, потому что они почти все ушли наружу. И в то же время клетка переполняется ионами калия, которые в неё накачали молекулярные насосы. Если бы мы могли попробовать на вкус цитоплазму клетки, мы бы заметили, что в результате работы насосов-обменников она превратилась из солёной в горько-солёно-кислую, потому что солёный вкус хлорида натрия сменился сложным вкусом довольно-таки концентрированного раствора хлорида калия. В клетке концентрация калия достигает 0,4 моль/л. Растворы хлорида калия в пределах 0,009–0,02 моль/л имеют сладкий вкус, 0,03–0,04 — горький, 0,05–0,1 — горько-солёный, а начиная с 0,2 и выше — сложный вкус, состоящий из солёного, горького и кислого [8].
Важно здесь то, что обмен натрия на калий — неравный. За каждые отданные клеткой три иона натрия она получает всего два иона калия. Это приводит к потере одного положительного заряда при каждом акте ионного обмена. Так что уже на этом этапе за счёт неравноценного обмена клетка теряет больше «плюсов», чем получает взамен. В электрическом выражении это составляет примерно −10 мВ отрицательности внутри клетки. (Но помните, что нам надо ещё найти объяснение для оставшихся −60 мВ!)
Чтобы легче было запомнить работу насосов-обменников, образно можно выразиться так: «Клетка любит калий!» Поэтому клетка и затаскивает калий к себе, несмотря на то, что его и так в ней полно. И поэтому она невыгодно обменивает его на натрий, отдавая 3 иона натрия за 2 иона калия. И поэтому она тратит на этот обмен энергию АТФ. И как тратит! До 70% всех энергозатрат нейрона может уходить на работу натрий-калиевых насосов. (Вот что делает любовь, пусть она даже и не настоящая!)
Кстати, интересно, что клетка не рождается с готовым потенциалом покоя. Ей его ещё надо создать. Например, при дифференцировке и слиянии миобластов потенциал их мембраны изменяется от −10 до −70 мВ, т.е. их мембрана становится более отрицательной — поляризуется в процессе дифференцировки. А в экспериментах на мультипотентных мезенхимальных стромальных клетках костного мозга человека искусственная деполяризация, противодействующая потенциалу покоя и уменьшающая отрицательность клеток, даже ингибировала (угнетала) дифференцировку клеток [1].
Образно говоря, можно выразиться так: Создавая потенциал покоя, клетка «заряжается любовью». Это любовь к двум вещам:
- любовь клетки к калию (поэтому клетка насильно затаскивает его к себе);
- любовь калия к свободе (поэтому калий покидает захватившую его клетку).
Механизм насыщения клетки калием мы уже объяснили (это работа насосов-обменников), а механизм ухода калия из клетки объясним ниже, когда перейдём к описанию второго этапа создания внутриклеточной отрицательности. Итак, результат деятельности мембранных ионных насосов-обменников на первом этапе формирования потенциала покоя таков:
- Дефицит натрия (Na+) в клетке.
- Избыток калия (K+) в клетке.
- Появление на мембране слабого электрического потенциала (−10 мВ).
Можно сказать так: на первом этапе ионные насосы мембраны создают разность концентраций ионов, или градиент (перепад) концентрации, между внутриклеточной и внеклеточной средой.
Второй этап создания отрицательности: утечка ионов K+ из клетки
Итак, что начинается в клетке после того, как с ионами поработают её мембранные натрий-калиевые насосы-обменники?
Из-за образовавшегося дефицита натрия внутри клетки этот ион при каждом удобном случае норовит устремиться внутрь: растворённые вещества всегда стремятся выровнять свою концентрацию во всём объёме раствора. Но это у натрия получается плохо, поскольку ионные натриевые каналы обычно закрыты и открываются только при определённых условиях: под воздействием специальных веществ (трансмиттеров) или при уменьшении отрицательности в клетке (деполяризации мембраны).
В то же время в клетке имеется избыток ионов калия по сравнению с наружной средой — потому что насосы мембраны насильно накачали его в клетку. И он, тоже стремясь уравнять свою концентрацию внутри и снаружи, норовит, напротив, выйти из клетки. И это у него получается!
Тут ещё важно понять то, что ионы натрия и калия как бы «не замечают» друг друга, они реагируют только «на самих себя». Т.е. натрий реагирует на концентрацию натрия же, но «не обращает внимания» на то, сколько вокруг калия. И наоборот, калий реагирует только на концентрацию калия и «не замечает» натрий. Получается, что для понимания поведения ионов надо по отдельности рассматривать концентрации ионов натрия и калия. Т.е. надо отдельно сравнить концентрацию по натрию внутри и снаружи клетки и отдельно — концентрацию по калию внутри и снаружи клетки, но не имеет смысла сравнивать натрий с калием, как это, бывает, делается в учебниках.
По закону выравнивания химических концентраций, который действует в растворах, натрий «хочет» снаружи войти в клетку; туда же его влечёт и электрическая сила (как мы помним, цитоплазма заряжена отрицательно). Хотеть-то он хочет, но не может, так как мембрана в обычном состоянии плохо его пропускает. Натриевые ионные каналы, имеющиеся в мембране, в норме закрыты. Если все же его заходит немножко, то клетка сразу же обменивает его на наружный калий с помощью своих натрий-калиевых насосов-обменников. Получается, что ионы натрия проходят через клетку как бы транзитом и не задерживаются в ней. Поэтому натрий в нейронах всегда в дефиците.
А вот калий как раз может легко выходить из клетки наружу! В клетке его полно, и она его удержать не может. Он выходит наружу через особые каналы в мембране — «калиевые каналы утечки», которые в норме открыты и выпускают калий [5, 7].
К+-каналы утечки постоянно открыты при нормальных значениях мембранного потенциала покоя и проявляют взрывы активности при сдвигах мембранного потенциала, которые длятся несколько минут и наблюдаются при всех значениях потенциала. Усиление К+-токов утечки ведёт к гиперполяризации мембраны, тогда как их подавление — к деполяризации. …Однако, существование канального механизма, ответственного за токи утечки, долгое время оставалось под вопросом. Только сейчас стало ясно, что калиевая утечка — это ток через специальные калиевые каналы.
От химического — к электрическому
А теперь — ещё раз самое главное. Мы должны осознанно перейти от движения химических частиц к движению электрических зарядов.
Калий (K+) положительно заряжен, и поэтому он, когда выходит из клетки, выносит из неё не только самого себя, но и положительный заряд. За ним изнутри клетки к мембране тянутся «минусы» — отрицательные заряды. Но они не могут просочиться через мембрану — в отличие от ионов калия — т.к. для них нет подходящих ионных каналов, и мембрана их не пропускает. Помните про оставшиеся необъяснёнными нами −60 мВ отрицательности? Это и есть та самая часть мембранного потенциала покоя, которую создаёт утечка ионов калия из клетки! И это — большая часть потенциала покоя.
Для этой составной части потенциала покоя есть даже специальное название — концентрационный потенциал [5]. Концентрационный потенциал — это часть потенциала покоя, созданная дефицитом положительных зарядов внутри клетки, образовавшимся за счёт утечки из неё положительных ионов калия.
Ну, а теперь немного физики, химии и математики для любителей точности.
Электрические силы связаны с химическими по уравнению Гольдмана. Его частным случаем является более простое уравнение Нернста, по формуле которого можно рассчитать трансмембранную диффузионную разность потенциалов на основе различной концентрации ионов одного вида по разные стороны мембраны. Так, зная концентрацию ионов калия снаружи и внутри клетки, можно рассчитать калиевый равновесный потенциал EK:
где Ек — равновесный потенциал, R — газовая постоянная, Т — абсолютная температура, F — постоянная Фарадея, К+внеш и K+внутр — концентрации ионов К+ снаружи и внутри клетки, соответственно. По формуле видно, что для расчёта потенциала между собой сравниваются концентрации ионов одного вида — K+.
Более точно итоговая величина суммарного диффузионного потенциала, который создаётся утечкой нескольких видов ионов, рассчитывается по формуле Гольдмана-Ходжкина-Катца. В ней учтено, что потенциал покоя зависит от трех факторов: (1) полярности электрического заряда каждого иона; (2) проницаемости мембраны Р для каждого иона; (3) [концентраций соответствующих ионов] внутри (внутр) и снаружи мембраны (внеш). Для мембраны аксона кальмара в покое отношение проводимостей РK : PNa :PCl = 1 : 0,04 : 0,45 [5].
Заключение
Итак, поте нциал покоя состоит из двух частей:
- −10 мВ, которые получаются от «несимметричной» работы мембранного насоса-обменника (ведь он больше выкачивает из клетки положительных зарядов (Na+), чем закачивает обратно с калием).
- Вторая часть — это всё время утекающий из клетки калий, уносящий положительные заряды. Его вклад — основной: −60 мВ. В сумме это и дает искомые −70 мВ.
Что интересно, калий перестанет выходить из клетки (точнее, его вход и выход уравниваются) только при уровне отрицательности клетки −90 мВ. В этом случае сравняются химические и электрические силы, проталкивающие калий через мембрану, но направляющие его в противоположные стороны. Но этому мешает постоянно подтекающий в клетку натрий, который несёт с собой положительные заряды и уменьшает отрицательность, за которую «борется» калий. И в итоге в клетке поддерживается равновесное состояние на уровне −70 мВ.
Вот теперь мембранный потенциал покоя окончательно сформирован.
Схема работы Na+/K+-АТФазы наглядно иллюстрирует «несимметричный» обмен Na+ на K+: выкачивание избыточного «плюса» в каждом цикле работы фермента приводит к отрицательному заряжению внутренней поверхности мембраны. Чего в этом ролике не сказано, так это того, что АТФаза ответственна за менее чем 20% потенциала покоя (−10 мВ): оставшаяся «отрицательность» (−60 мВ) появляется за счет выхода из клетки через «калиевые каналы утечки» ионов K+, стремящихся выровнять свою концентрацию внутри клетки и вне нее.
- Jacqueline Fischer-Lougheed, Jian-Hui Liu, Estelle Espinos, David Mordasini, Charles R. Bader, et. al.. (2001). Human Myoblast Fusion Requires Expression of Functional Inward Rectifier Kir2.1 Channels. J Cell Biol. 153, 677-686;
- Liu J.H., Bijlenga P., Fischer-Lougheed J. et al. (1998). Role of an inward rectifier K+ current and of hyperpolarization in human myoblast fusion. J. Physiol. 510, 467–476;
- Sarah Sundelacruz, Michael Levin, David L. Kaplan. (2008). Membrane Potential Controls Adipogenic and Osteogenic Differentiation of Mesenchymal Stem Cells. PLoS ONE. 3, e3737;
- Павловская М.В. и Мамыкин А.И. Электростатика. Диэлектрики и проводники в электрическом поле. Постоянный ток / Электронное пособие по общему курсу физики. СПб: Санкт-Петербургский государственный электротехнический университет;
- Ноздрачёв А.Д., Баженов Ю.И., Баранникова И.А., Батуев А.С. и др. Начала физиологии: Учебник для вузов / Под ред. акад. А.Д. Ноздрачёва. СПб: Лань, 2001. — 1088 с.;
- Макаров А.М. и Лунева Л.А. Основы электромагнетизма / Физика в техническом университете. Т. 3;
- Зефиров А.Л. и Ситдикова Г.Ф. Ионные каналы возбудимой клетки (структура, функция, патология). Казань: Арт-кафе, 2010. — 271 с.;
- Родина Т.Г. Сенсорный анализ продовольственных товаров. Учебник для студентов вузов. М.: Академия, 2004. — 208 с.;
- Кольман Я. и Рем К.-Г. Наглядная биохимия. М.: Мир, 2004. — 469 с.;
- Шульговский В.В. Основы нейрофизиологии: Учебное пособие для студентов вузов. М.: Аспект Пресс, 2000. — 277 с..
Все живые клетки
при действии различных раздражителей
(химических, механических, температурных
и пр.) способны переходить в возбужденное
состояние. Опыт показывает, что
возбужденный участок становится
электроотрицательным по отношению к
покоящемуся, что является показателем
перераспределения ионных потоков в
возбужденном участке. Реверсия потенциала
при возбуждении кратковременна, и после
окончания возбуждения через некоторое
время вновь восстанавливается исходный
потенциал покоя. Общее изменение разности
потенциалов на мембране, происходящее
при возбуждении клеток, называется
потенциалом действия. На рис. 11.17
представлен потенциал действия
гигантского аксона кальмара, обозначены
отдельные стадии изменения потенциала.
В частности, для клетки характерен так
называемый запаздывающий потенциал,
когда в течение некоторого времени на
мембране существует даже меньший
потенциал, чем потенциал покоя.
Было показано, что
возбуждение связано с увеличением
электропроводности клеточной мембраны.
При этом временная зависимость
электропроводимости повторяла форму
потенциала действия. Чтобы решить
вопрос, для каких ионов изменяется
проницаемость м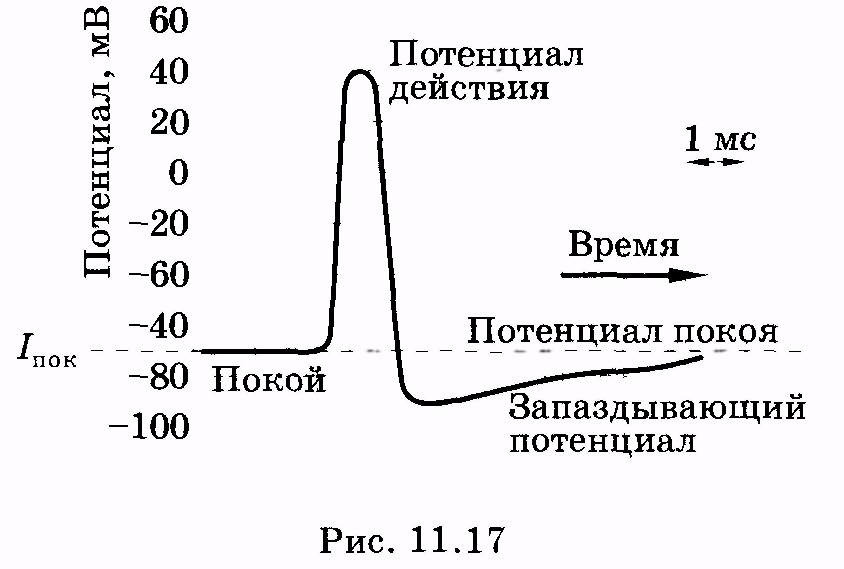
следует обратить внимание, что потенциал
действия приводит к кратковременному
возрастанию потенциала внутри клетки
(см. рис. 11.17). Отрицательный относительно
внешней среды потенциал становится
положительным. Если по уравнению Нернста
(11.38) вычислить равновесные потенциалы
на мембране аксона кальмара, то получим
соответственно для ионов К+, Na+ и Сl—величины -90, +46 и -29 мВ. Так как при
изменении проницаемости мембраны для
какого-либо иона этот ион будет проникать
через нее, стремясь создать равновесное
состояние, то числовые данные показывают,
что внутрь клетки проникают ионы Na+,
создавая там положительный потенциал.
Следовательно, при возбуждении клетки
в начальный период увеличивается
проницаемость мембран именно для ионов
натрия. «Натриевая теория» возникновения
потенциала действия была предложена,
разработана и экспериментально
подтверждена А. Ходжкином и А. Хаксли,
за что в 1963 г. они были удостоены
Нобелевской премии.
Измерить проницаемость
мембран для какого-либо иона (иначе
говоря, электропроводимость или
сопротивление мембраны для этого иона)
можно, если на основании закона Ома
найти отношение тока к напряжению, или
наоборот. Практическая реализация такой
задачи осложняется тем, что проницаемость
(электрическое сопротивление) мембраны
при возбуждении изменяется со временем.
Это приводит к перераспределению
электрического напряжения в цепи, и
разность потенциалов на мембране
изменяется. Ходжкин, Хаксли и Катц смогли
создать опыт с фиксацией определенного
значения разности потенциала на мембране.
Это позволило им провести измерение
ионных токов и, следовательно, проницаемости
(сопротивления) мембран для ионов.
Оказалось, что отношение проницаемостей
мембраны для ионов натрия и калия
практически повторяет форму потенциала
действия. Кроме того, были получены
кривые временной зависимости ионных
токов через мембрану (рис. 11.18). На этом
рисунке кривая 1соответствует
временной зависимости суммарного
ионного тока через мембрану гигантского
аксона кальмара, полученного при
изменении потенциала на мембране до
+56 мВ (потенциал покоя равен60
мВ). Вначале направление тока отрицательно,
что соответствует прохождению
положительных ионов через мембрану
клетки. Было установлено, что ток этот
обусловлен прохождением ионов натрия
внутрь клетки, где концентрация их
значительно меньше, чем снаружи.
Естественно, что
при таком нарушении равновесия ионы
калия начнут перемещаться наружу, где
их концентрация существенно меньше.
Для того чтобы выяснить, какая часть
тока «натриевая», а какая «калиевая»,
можно провести то же возбуждение, но в
искусственных условиях, когда в среде,
окружающей аксон, нет натрия. В этом
случае (см. кривую 2) ток обусловливается
только выходом ионов калия наружу из
клетки. Разница значений тока для двух
кривых показана на кривой3: кривая3есть разность кривых1и2.
Она дает зависимость от времени ионного
тока натрия. На этой кривой частьасоответствует открыванию натриевых
каналов, аб— их закрытию
(инактивации).
В целом
последовательность событий, происходящих
на клеточной мембране при возбуждении,
выглядит следующим образом. При
возбуждении в мембране открываются
каналы для ионов натрия (проницаемость
мембраны возрастает более чем в 5000 раз).
В результате отрицательный заряд с
внутренней стороны мембраны становится
положительным, что соответствует пику
мембранного потенциала (фаза деполяризации
мембраны). Затем поступление натрия из
внешней среды прекращается. В это время
натриевые каналы закрываются, но
открываются калиевые. Калий проходит
в соответствии с градиентом концентрации
из клетки до тех пор, пока не восстановится
первоначальный отрицательный заряд на
мембране и мембранный потенциал не
достигнет своего первоначального
значения (фаза реполяризации). На самом
деле выход ионов калия из клетки
продолжается дольше, чем это требуется
для восстановления потенциала покоя.
В результате за пиком потенциала действия
следует небольшой минимум (запаздывающий
потенциал).
Ионные
каналы имеют белковое происхождение
(см. рис. 11.3 и 11.13). Они селективно
(выборочно) пропускают ионы разного
вида. Канал может быть «закрыт»
(блокирован) молекулами ядов, его
пропускная способность зависит от
действия некоторых лекарственных
средств. Поэтому теория ионных каналов
в мембранах является важной частью
молекулярной фармакологии.
Механизм распространения потенциала
действия в деталях рассматривается в
курсе нормальной физиологии. Мы же
рассмотрим лишь некоторые основные
положения. Распространение потенциала
действия вдоль нервного волокна (аксона)
обусловлено возникновением так называемыхлокальных токов, образующихся
между возбужденным и невозбужденным
участками клетки. На рис. 11.19 схематично
указаны отдельные стадии возникновения
и распространения потенциала действия.
В состоянии покоя (рис. 11.19, а) внешняя
поверхность клеточной мембраны имеет
положительный потенциал, а внутренняя
— отрицательный. В момент возбуждения
полярность мембраны меняется на
противоположную (рис. 11.19,б). В
результате этого между возбужденным и
невозбужденным участками мембраны
возникает разность потенциалов. Наличие
разности потенциалов и приводит к
появлению между этими участкамилокальных
токов. На поверхности клетки локальный
ток течет от невозбужденного участка
к возбужденному; внутри клетки он течет
в обратном направлении (рис. 11.19, в).
Локальный ток, как и любой электрический
ток, раздражает соседние невозбужденные
участки и вызывает увеличение проницаемости
мембраны. Это приводит к возникновению
потенциалов действия в соседних участках.
В то же время в ранее возбужденном
участке происходят восстановительные
процессы реполяризации. Вновь возбужденный
участок в свою очередь становится
электроотрицательным и возникающий
локальный ток раздражает следующий
за ним участок. Этот процесс многократно
повторяется и обусловливает распространение
импульсов возбуждения по всей длине
клетки в обоих направлениях (рис. 11.19,г). В нервной системе импульсы
проходят лишь в определенном
направлении из-за наличия синапсов,
обладающих односторонней проводимостью.
По
электрическим свойствам аксон напоминает
кабель с проводящей сердцевиной и
изолирующей оболочкой. Однако для того
чтобы в кабеле не было значительных
потерь энергии при протекании
тока, сопротивление его должно быть
малым, а сопротивление
изоляции — очень большим. В аксоне
проводящим веществом
служит аксоплазма, т. е. раствор
электролита, удельноесопротивление
которого в миллионыраз
больше, чем у меди или алюминия,
из которых изготавливают обычные
кабели. Удельное сопротивление биомембран
достаточно велико, но вследствие их
малой толщины сопротивление изоляции
«аксонного кабеля» в сотни тысяч раз
меньше, чем у технического кабеля. По
этой причине однородное н
волокно не может проводить электрический
сигнал на далекое расстояние, интенсивность
сигнала быстро затухает. Расчеты
показывают, что напряжение на мембране
волокна будет экспоненциально уменьшаться
по мере удаления от места возбуждения
(рис. 11.20). Если величина потенциала
действия в месте возбуждения была равна mах,
то на расстоянии l
от этого места потенциал на мембране
будет равен:
(11.40)
где
—
постоянная
длины нервного
волокна, которая определяет степень
затухания сигнала в аксоне по
экспоненциальному закону. Эту величину
можно рассчитать по следующей приближеннойформуле:
(11.41)
где
d
— диаметр
волокна, R
— поверхностное
сопротивление мембраны
в Ом • м2
(т. е. сопротивление 1 м2
ее поверхности) и
— удельное сопротивление аксоплазмы
в Ом • м.
Расчеты,
проведенные для аксона кальмара,
показывают, что на
конце аксона величина сигнала должна
быть ничтожно малой. Однако
существование локальных токов приводит
к тому, что возбуждение
передается по нервному волокну без
затухания. Это объясняется тем, что
локальные токи лишь деполяризуют
мембрану до
критического уровня, а потенциалы
действия в каждом участке
мембраны поддерживаются независимыми
ионными потоками, перпендикулярными
к направлению распространения возбуждения.
Из
(11.40) видно, что с увеличением
степень затухания сигнала
уменьшается. Было показано, что при этом
возрастает скорость проведения импульса,
а это очень важно для жизнедеятельности
любого организма. Величины
и
примерно одинаковы
для всех животных
клеток, и поэтому увеличения постоянной
длины
можно добиться путем увеличения диаметра
d
аксона. Именно
поэтому у кальмаров аксоны достигают
«гигантских» размеров (диаметр до 0,5
мм), что обеспечивает кальмару достаточно
быстрое проведение нервного импульса
и, следовательно, быстроту реакции
на внешние раздражители.
У
нервной системой
толстые волокна оказываются неэкономичными,
и затухание сигнала предотвращается
другим способом. Мембраны аксонов у них
покрытымиелином — веществом,
содержащим много холестерина и мало
белка (рис. 11.21). Удельное сопротивление
миелина значительно
выше удельного сопротивления других
биологических мембран. Помимо этого,
толщина миелиновой оболочки во много
раз больше толщины обычной мембраны,
что приводит к возрастанию диаметра
волокна и соответственно величины.
Как видно из рис. 11.21, миелиновая оболочка
не полностью покрывает
все волокно; оно разделено на отдельные
сегменты, между которыми на участках
длиной около 1 мкм мембрана аксона
непосредственно соприкасается с
внеклеточным раствором. Области, вкоторых мембрана
контактирует с раствором, называют
перехватами Ранвье. В связи с
большим сопротивлением миелиновой
оболочки по поверхности
аксона токи протекать не могут, и
затухание сигнала резко уменьшается.
При возбуждении одного узла возникают
токи между ним и другими узлами. Ток,
подошедший к другому узлу, возбуждает
его, вызывает появление в этом местепотенциала действия,
и процесс распространяется по всему
волокну. Затраты энергии на
распространение сигнала по волокну,покрытому миелином,
значительно меньше, чем по
немиелинизированному, так как общее
количество ионов натрия, проходящих
через мембрану
в области узлов, значительно меньше,
чем если бы они проходили через всю
поверхность мембраны. При некоторых
заболеваниях структура миелиновых
оболочек нарушается, и это
приводит к нарушению проведения нервного
возбуждения. При блокировании узлов
нервного волокна анестезирующими
средствами, например ядом кураре,
сопротивление аксона возрастает и
прохождение сигналов по нерву замедляется
или совсемпрекращается.
Поскольку
узлы замыкаются через аксоплазму и
внеклеточную
среду, то можно предположить, что при
увеличении сопротивления внешней среды
скорость проведения нервного импульса
уменьшится. Это предположение было
проверено на опыте. Нервные
волокна сначала помещали в морскую
воду, а затем в масло с большим удельным
сопротивлением. Скорость проведения
импульса во втором случае уменьшалась
в 1,5—2 раза (в зависимости от диаметра
волокна).
Существует
некоторая формальная аналогия между
распространением потенциала действия
по нервному волокну и электромагнитной
волной в двухпроводной линии или
коаксиальном кабеле. Однако между этими
процессами имеется существенное
различие.Электромагнитная
волна, распространяясь в среде, ослабевает,
так как растрачивает свою энергию.
Волна возбуждения, проходящая
по нервному волокну, не затухает, получая
энергию в самой
среде (энергию заряженной мембраны).
Волны, получающие энергию из среды
в процессе распространения, называютавтоволнами,
а среду —
активно-возбудимой
средой (ABC).
В § 11.9
будут рассмотрены более подробно
свойства авто волн, распространяющихся
в ABC.
Соседние файлы в папке лабораторные 1 семестр
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Управление проектами Фукс.docx
§ 2. Мембранный потенциал в аксоне кальмара
Гипотеза о том, что в основе мембранного потенциала лежит различие между внеклеточной и внутриклеточной концентрациями калия, была впервые высказана Бернштейном 1) в 1902 г. Ему не удалось проверить свое предположение экспериментально, поскольку в то время не существовало способа измерения мембранного потенциала. В наши дни можно с высокой точностью измерить мембранный потенциал, а также убедиться в том, что изменения концентрации калия внутри и снаружи клетки приводят к изменениям мембранного потенциала в соответствии с предсказаниями уравнения Нернста.
Впервые такие измерения были проведены на гигантском аксоне кальмара. Аксон этот достигает 1 ммоль в диаметре 2), что позволяет вводить в него электроды с целью прямого измерения мембранного потенциала (рис. 5.3А). Более того, аксон кальмара удивительно живуч и продолжает функционировать, даже если из него выдавить цитоплазму с помощью резинового валика и заменить ее на перфузионный раствор (рис. 5.3В и С). У исследователя есть возможность контролировать ионный состав как внеклеточного, так и внутриклеточного растворов. А. Л. Ходжкин, вместе с А. Ф. Хаксли впервые поставивший многие эксперименты на аксоне кальмара (за которые они позже были удостоены Нобелевской премии), однажды сказал 3):
Можно утверждать, что введение Юнгом в 1936 году препарата аксона кальмара имело для науки об аксоне большее значение, чем какое-либо другое открытие, сделанное за последние 40 лет. Один выдающийся нейрофизиолог заметил недавно во время ужина на одном из конгрессов (не самым тактичным образом, должен признать): «Если честно. Нобелевскую премию нужно было присвоить кальмару».
Концентрации основных ионов в крови кальмара, а также в цитоплазме его аксона, приведены в табл. 5.1 (такие ионы, как магний и внутриклеточные анионы, опущены). Эксперименты на изолированном аксоне обычно проводятся в морской воде, соотношение концентраций калия во внутриклеточной и внеклеточной средах составляет при этом 40 : 1.
Глава 5. Ионные механизмы потенциала покоя 93

|
Рис. 5.3. Электрическое отведение от аксона кальмара. (А) Фотография изолированного аксона кальмара с введенным в него электродом. (В) Удаление аксоплазмы из аксона, который затем наполняется внутриклеточным перфузионным раствором. (С) Сопоставление отведений после (perfused) и до (intact) перфузии показывает, что удаление аксоплазмы не влияет как на потенциал покоя, так и на потенциал действия.
Fig. 5.3. Recording from a Squid Ахоп. (A) Isolated giant axon of the squid, with axial recording electrode inside. (B) Extrusion of axoplasm from the axon, which is then cannulated and perfused internally. (C) Comparison of records before (intact) and after perfusion shows that the resting and action potentials are unaffected by removal of the axoplasm. (A from Hodgkin and Keynes 1956; В and С after Baker, Hodgkin, and Shaw, 1962.) |
Если бы мембранный потенциал был равен равновесному потенциалу для калия, его значение было бы –93 мВ. В действительности мембранный потенциал гораздо менее отрицателен (от –65 до –70 мВ). С другой стороны, это значение более отрицательно, чем равновесный потенциал для хлора (+55 мВ). Гипотеза Бернштейна была проверена путем измерения потенциала покоя и сравнения его с калиевым равновесным потенциалом при различных значениях внеклеточной концентрации калия. Заметим, что, как и в случае модели идеальной клетки, изменения уровня калия снаружи не влекут за собой значительных изменений его внутриклеточной концентрации. Из уравнения Нернста следует, что изменение концентрационного градиента в 10 раз при комнатной температуре приведет к изменению мембранного потенциала на 58 мВ. Результат эксперимента по варьированию внеклеточного уровня калия показан на рис. 5.4. На оси абсцисс представлен логарифм внеклеточной концентрации калия, а на оси ординат — мембранный потенциал.
94 Раздел II. Передача информации в нервной системе
Таблица 5.1. Концентрации ионов снаружи и внутри аксонов кальмара.
Table 5.1. Concentrations of ions inside and outside freshly isolated axons of squid.
| ion | Concentration (ммоль) | ||
| Axoplasm | Blood | Scawater | |
| Potassium | 400 | 20 | 10 |
| Sodium | 50 | 440 | 460 |
| Chloride | 60 | 560 | 540 |
| Calcium | 0,1 мкМа | 10 | 10 |
| Source: After Hodjkin, 1964. | |||
| а∙ Ionized intracellular calcium from Baker, Hodgkin, and Ridgeway, 1971. |
Теоретически предсказанный угол наклона кривой (соответствующий изменению потенциала на 58 мВ при десятикратном изменении концентрации и показанный прямой линией) в действительности достигается лишь при сравнительно высоких концентрациях. Чем ниже концентрация калия, тем меньше угол наклона кривой. Данные показывают, что распределение ионов калия не является единственным фактором, формирующим мембранный потенциал.
Роль натриевой проницаемости
Из экспериментов на аксоне кальмара можно заключить, что гипотеза, высказанная Бернштейном в 1902 г., была близка к истине: трансмембранный градиент калия является важным, хотя и не единственным фактором, влияющим на мембранный потенциал. Чем можно объяснить отклонение экспериментальной кривой, показанной на рис. 5.4, от уравнения Нернста? Оказывается, для этого достаточно снять ограничение с модели, состоящее в том, что мембрана непроницаема для ионов натрия. Мембрана реальной клетки действительно обладает натриевой проницаемостью, которая составляет от 1 до 10 % калиевой.
Для рассмотрения роли натриевой проницаемости обратимся к модели идеальной клетки и временно исключим из поля зрения перемещение ионов хлора. Мембранный потенциал равен калиевому равновесному потенциалу, поэтому перемещение суммарного заряда через мембрану отсутствует, клетка находится в покое. Если теперь ввести в модель натриевую проницаемость, то натрий будет стремиться войти в клетку благодаря как своему концентрационному градиенту, так и мембранному потенциалу. По мере входа натрия на внутренней поверхности мембраны накапливается положительный заряд и мембрана деполяризуется. В результате ионы калия выходят из равновесия и начинают покидать клетку. С увеличением деполяризации мембраны движущая сила для входа натрия снижается, в то время как движущая сила для выхода калия возрастает. Процесс продолжается до тех пор, пока оба ионных потока не уравновесят друг друга. В этот момент изменение мембранного потенциала прекращается, поскольку какое-либо накопление заряда отсутствует. Вообще говоря, значение мембранного потенциала расположено между калиевым и натриевым равновесными потенциалами и определяется равновесием между калиевым и натриевым токами, равными по величине и направленными в противоположные стороны.
Ионы хлора также участвуют в этом процессе, однако, как мы убедились ранее, равновесный потенциал для хлора подстраивается под новое значение мембранного потенциала за счет изменения внутриклеточной концентрации этого иона. По мере того как токи катионов постепенно приходят в равновесие, внутриклеточный уровень хлора возрастает до тех пор, пока суммарный хлорный ток не станет равным нулю.
Уравнение постоянного поля
Для того чтобы вычислить точное значение мембранного потенциала для модели идеальной клетки, необходимо принять во внимание отдельные ионные токи, протекающие через мембрану. Входящий натриевый ток (iNa) зависит от величины движущей силы для ионов натрия (Vm—ENa) (глава 2), а также от натриевой проводимости мембраны (gNa). Проводи-
Глава 5. Ионные механизмы потенциала покоя 95
| Рис. 5.4. Зависимость мембранного потенциала от внеклеточной концентрации калия на аксоне кальмара (полу-логарифмическая шкала). Прямая линия проведена под углом наклона, равным 58 мВ на десятикратное изменение внеклеточного уровня калия, в соответствии с уравнением Нернста. Благодаря наличию мембранной проницаемости для натрия, экспериментальные данные расходятся с прямой линий, особенно при низких концентрациях калия.
Fig. 5.4. Membrane Potential versus External Potassium Concentration in squid ixon, plotted on a semilogarithmic scale. The straight line is drawn with a slope of 58 mV per 10-fold change in extracellular potassium concentration, according to the Nernst equation. Because the membrane is also permeable to sodium, the points deviate from the straight line, especially at low potassium concentrations. (After Hodgkin and Keynes, 1955.) |
 |
мость пропорциональна среднему количеству натриевых каналов, находящихся в открытом состоянии при потенциале покоя: чем больше открытых каналов, тем выше проводимость. Таким образом, натриевый ток равен:
Тот же подход справедлив и для калия и хлора:
Если принять iCl, = 0 (т. е. ионы хлора находятся в равновесии), то, для сохранения неизменного значения мембранного потенциала, калиевый и натриевый токи должны быть равны по величине и противоположны по направлению:
Рассмотрим это уравнение более подробно. Предположим, что gKзначительно больше gNa. Тогда, для того чтобы токи были равны, движущая сила для выхода калия должна быть значительно меньше движущей силы для натриевого входа. Другими словами, мембранный потенциал должен быть ближе к ЕK , чем к ENa. Соответственно, если значение gNa велико, то мембранный потенциал будет ближе к ENa.
Преобразовав выражение, получим формулу для мембранного потенциала:
Если по той или иной причине ионы хлора не находятся в равновесии, то формула приобретает несколько более сложный вид:
Вышеприведенные расчеты были первоначально проведены Голдманом4) и, независимо от него, Ходжкином и Катцем5), с той лишь разницей, что вместо равновесных потенциалов и проводимостей они оперировали ионными концентрациями снаружи ([Na]0,…) и внутри ([Na]i,…) клетки, а также проницаемостью мембраны для каждого из ионов (pNa···):
Так же как и ранее, хлорные компоненты выражения не рассматриваются, если ионы хлора находятся в равновесии. Уравнение называется «уравнением ГХК» по фамилиям авторов, или уравнением постоянного поля, поскольку одним из допущений при выводе уравнения является равномерное распределение градиента напряжения (т.е. «поля») на всем протяжении мембраны. Уравнение ГХК полностью аналогично уравнению проводимостей, на его основании можно сделать те же предсказания: когда проницаемости для натрия и хлора малы по сравнению с калиевой проницаемостью, хлорный и натриевый компоненты уравнения становятся пренебрежимо малы, и мембранный потенциал стремится к значению равновесного потенциала для
96 Раздел II. Передача информации в нервной системе
 |
Рис. 5.5. Пассивные ионные токи и работа насосов в состоянии покоя. Пунктирные стрелки указывают направление пассивного движения ионов через мембрану клетки, а сплошные — направление переноса ионов транспортными системами. Длина стрелки отражает относительную величину суммарного переноса заряда. Суммарный ток для каждого иона равен нулю. Например, суммарный пассивный вход натрия равен по величине транспорту этого иона из клетки наружу. Транспорт Na : К осуществляется в соотношении 3 : 2. В зависимости от конкретной клетки транспорт хлора может быть выходящим (как показано на рисунке) или входящим. |
Fig. 5.5. Passive Ion Fluxes and Pumps in a Steady State. Net passive ion movements across the membrane are indicated by dashed arrows, transport systems by solid arrows and circles. Lengths of arrows indicate the relative magnitudes of net ion movements. Total flux is zero for each ion. For example, the net inward leak of Na+ is equal to the rate of outward transport. Na : К transport is coupled with a ratio of 3 : 2. In any particular cell. Cl—transport may be outward (as shown) or inward.
калия: Vm = 58 log([K]0/[K]1). При увеличении натриевой проницаемости мембранный потенциал сдвигается в сторону натриевого равновесного потенциала.
Из уравнения постоянного поля следует один важный принцип. Мембранный потенциал зависит от проводимости (или проницаемости) мембраны для важнейших ионов, а также от их равновесных потенциалов. В реальных клетках проводимости для калия и хлора сравнительно· высоки, поэтому потенциал покоя клетки близок к равновесным потенциалам для этих двух ионов. При увеличении натриевой проводимости, например, во время потенциала действия (глава 6) или возбуждающего постсинаптического потенциала (глава 9), мембранный потенциал сдвигается в сторону натриевого равновесного потенциала.
Потенциал покоя
Несмотря на то, что во многих случаях уравнение ГХК. весьма полезно, оно не дает возможности правильно вычислить потенциал покоя. Дело в том, что условие равенства суммарного тока нулю неправомочно: третье условие равновесия, а именно требование, чтобы каждый отдельный ионный ток равнялся нулю, не выполняется. В результате клетка будет постепенно терять калий и наполняться натрием и хлором. В реальных клетках концентрации натрия и калия поддерживаются на постоянном уровне при помощи натрий-калиевых насосов (глава 4). В противовес непрерывному потоку натрия внутрь клетки и калия наружу, эти насосы переносят оба эти иона в определенной пропорции в направлении, противоположном их пассивному движению (рис. 5.5). Следовательно, для поддержания клетки в стабильном состоянии затрачивается метаболическая энергия.
Чтобы получить более полную формулу потенциала покоя, необходимо принять во внимание как пассивное движение ионов, так и их активный транспорт, осуществляемый насосами. Рассмотрим сначала пассивное движение ионов натрия и калия через мембрану:
Отказавшись от предположения о том, что токи эти равны по величине и противоположны по направлению, но зная соотношение между ними, можно получить уравнение мембранного потенциала, исходя из равновесных потенциалов для натрия и калия, а также их относительных проводимостей. Здесь уже нужно учитывать влияние насоса. Поскольку насос поддерживает внутриклеточные концентрации натрия и калия на постоянном уровне, перенося ионы в соотношении 3 : 2, то и пассивные токи должны находиться в том же соотношении: iNa/iK = 3/2. Имеем следующее выражение:
Соотношение имеет отрицательную величину, потому что направления натриевого и калиевого токов противоположны. Преобразовав выражение, получим:
Это уравнение похоже на полученное выше для модели идеальной клетки, и на его
Глава 5. Ионные механизмы потенциала покоя 97
основании можно сделать то же предсказание: значение мембранного потенциала будет определяться относительными величинами gNa и gК. Отличие настоящей формулы состоит в том, что члены, относящиеся к калию, умножены на 1,5. Благодаря этому фактору мембранный потенциал будет ближе к EK. Таким образом, движущая сила для входа натрия возрастает, а для выхода калия, наоборот, уменьшается. В результате и пассивные токи натрия и калия будут находиться в соотношении 3 : 2, а не 1:1.4,
Обобщая вышесказанное, можно сделать вывод, что потенциал покоя — это такое значение мембранного потенциала, при котором входящий натриевый ток не равен по величине выходящему калиевому, а превосходит его в 1,5раза. Пассивные токи обоих ионов определяются их равновесными потенциалами и проводимостями, в то время как соотношение токов 3 : 2 продиктовано стехиометрическими характеристиками насоса.
Задачу по выводу формулы потенциала покоя для реальных клеток впервые взяли на себя Муллинс и Нода6). С помощью внутриклеточных микроэлектродов они исследовали влияние изменения ионных концентраций на мембранный потенциал мышечной клетки. Подобно Голдману, Ходжкину и Катцу, они получили выражение, связывающее мембранный потенциал с проницаемостями и концентрациями отдельных ионов. Результат аналогичен только что полученному нами уравнению, основанному на проводимостях и равновесных потенциалах:
где r — абсолютное значение соотношения ионного транспорта (3 : 2). Уравнение точно описывает потенциал покоя при условии, что все остальные ионы, проникающие сквозь мембрану (такие как хлор), находятся в равновесии.
Распределение хлора
Насколько применимы подобные рассуждения для хлора? Как и для других ионов, суммарный ток хлора должен быть равен нулю. Как показано выше (рис. 5.2В), равновесие ионов хлора достигается путем простого изменения его внутриклеточной концентрации, без изменения при этом мембранного потенциала. Тем не менее, во многих клетках существуют транспортные системы для хлора (глава 4). В аксоне кальмара и в мышце активные транспортные системы переносят ионы хлора внутрь клетки; во многих нервных клетках, напротив, хлор выводится из клетки (см. рис. 5.5). В результате активного транспорта хлора в клетку, его внутриклеточная концентрация возрастает, что приводит к усилению выходящего пассивного тока утечки хлора, равного по величине активному входящему току 7). Транспорт хлора из клетки наружу производит обратное действие.
Электрическая модель мембраны
Для тех, кто предпочитает иметь дело с электрическими схемами, вышеприведенные рассуждения показаны на рис. 5.6 в обобщенном виде. Потенциалы ENa, ЕKи ЕClпоказаны в виде батарей, а проводимости для натрия, калия и хлора изображены в виде сопротивлений (резисторов). Пассивные токи через сопротивления равны и противоположны токам, генерируемым соответствующими насосами, поэтому суммарный ток через мембрану для каждого иона равен нулю.
Ожидаемые значения мембранного потенциала
Можно ли, основываясь на вышеприведенных соображениях, объяснить нелинейную зависимость мембранного потенциала от концентрации калия, показанную иа рис. 5.4? Ответ станет очевидным, если подставить в формулу реальные значения. Для аксона кальмара соотношение констант проницаемости для натрия и калия приблизительно равно 0,04 : 1,0.5 Воспользовавшись этими данными, а также значениями ионных концентраций из табл. 5.1, получим потенциал покоя в морской воде:
Становится очевидным, почему при изменении внеклеточной концентрации калия мембранный потенциал не строго подчиняется уравнению Нернста для калия, как показано на рис. 5.4. Если сравнить слагаемые в знаменателе, относящиеся к калию ( 1,5 x 10 = 15) и к натрию (0,04 x 460 = 18,4), то получится, что вклад калия составляет всего около 45%. По этой причине, увеличение внеклеточной концентрации калия вдвое не приведет к удвоению числителя (как было бы
98 Раздел II. Передача информации в нервной системе
 |
Рис. 5.6. Электрическая схема мембраны клетки в состоянии равновесия, показанном на рис. 5.5. Ek, ENalи EСl — потенциалы Нернста для соответствующих ионов. Отдельные ионные проводимости представлены в виде сопротивлений (величина которых равна 1/gдля каждого иона). Отдельные ионные токи (iK , . . . ) равны по величине и противоположны по направлению токам, генерируемым натрий-калиевым обменником (ТNa—K) и хлорным насосом (ТCl ), поэтому суммарный ток через мембрану для каждого иона равен нулю. Vm— устанавливающийся в результате мембранный потенциал. |
Fig. 5.6. Electrical Model oflhe Steady-State Cell Membrane shown in Figure 5.5. ЕK, ЕNa, and EClare the Nernst potentials for the individual ions. The individual ion conductances are represented by resistors (having a resistance of 1/g for each ion). The individual ion currents (iK, iNa, and iNa) are equal and opposite to the currents (i T(K), iΤ(Na)’ and iT(Cl)) supplied by the sodium-potassium exchange pump (tna—k), and the chloride pump (Ta), so the net flux of each ion across the membrane is zero. The resulting membrane potential is Vm.
в случае полного соответствия с уравнением Нернста), и, следовательно, эффект изменения уровня калия на мембранный потенциал меньше, чем в идеальной ситуации, когда калий является единственным проводящим ионом. Когда внеклеточная концентрация калия возрастает до существенных значений (100 ммоль на рис. 5.4), то роль калиевого компонента в знаменателе становится подавляющей, и кривая зависимости приближается к своему теоретическому углу наклона (58 мВ на 10-кратное увеличение концентрации калия). Этот эффект усиливается благодаря свойству калиевых каналов, обсуждавшемуся в главе 3. Многие калиевые каналы обладают чувствительностью к мембранному потенциалу и открываются при деполяризации, вызванной увеличением внеклеточной концентрации калия. В результате подобного увеличения проницаемости для калия вклад натрия в формирование мембранного потенциала дополнительно снижается.
Вообще, потенциал покоя нервных клеток приблизительно равен -70 мВ. В некоторых клетках, например в скелетной мышце позвоночных 8), потенциал покоя может быть -90 мВ или даже больше, что объясняется значительным превосходством калиевой проводимости над натриевой. Натриевая проводимость глиальных клеток настолько мала, что их потенциал покоя практически равен калиевому равновесному потенциалу (глава 8). В таких клетках, как, например, нейроны ганглиев пиявки 9) или рецепторы сетчатки10), натриевая проводимость достаточно велика, а потенциал покоя составляет всего —40 мВ.
Вклад натрий-калиевого насоса в мембранный потенциал
Натрий-калиевый насос является электрогенным, потому что за каждый цикл его работы из клетки выводится один суммарный положительный заряд, тем самым увеличивая отрицательный заряд на внутренней поверхности мембраны клетки. Насколько велик этот вклад в заряд на мембране? Чтобы ответить на этот вопрос, представим себе, что насос не электрогенен, а нейтрален, то есть соотношение ионов, переносимых насосом внутрь и наружу клетки, равно единице. С учетом этого условия проведем вычисления:
Поскольку полученный потенциал покоя на 6 мВ менее отрицателен, то можно сделать вывод о том, что вклад насоса в потенциал покоя равен -6 мВ. При условии транспорта ионов в соотношении 3 : 2 вклад насоса в потенциал покоя не может превысить -11 мВ11). При остановке ионообмена его влияние на величину потенциала покоя прекращается, и потенциал покоя постепенно снижается по мере накопления в клетке ионов натрия и выхода из нее калия.
Ионные каналы, участвующие в формировании потенциала покоя
Наличие проводимости для натрия, калия и хлора в состоянии покоя было показано во многих клетках. Интересно отметить, что ионные каналы, обеспечивающие эти проводимости, до сих пор не были определены ни в одном типе клеток. Кандидаты
Глава 5. Ионные механизмы потенциала покоя 99
на роль калиевых каналов, активных в диапазоне потенциала покоя, различны в зависимости от типа клеток. Среди них есть каналы, активируемые внутриклеточными катионами: натрий-активируемые и кальций—активируемые калиевые каналы. Кроме того, многие нервные клетки обладают так называемым калиевым каналом типа «М», которые открыты при потенциале покоя и закрываются при участии внутриклеточных посредников (глава 16). Активация большого количества потенциалзависимых калиевых каналов (то есть «замедленного выпрямителя» — delayed rectifier, и каналов типа «А») при потенциале покоя маловероятна. Однако, даже 0,1-1 % от их общего числа было бы достаточно, чтобы создать проводимость, сравнимую с проводимостью в покое 12).
Конкретные носители натриевой проводимости в нервных клетках также неизвестны. В некоторой степени, вход натрия может происходить через калиевые каналы, для большинства из которых проницаемость для натрия составляет от 1 до 3 % от калиевой проницаемости 13). Кроме того, открытые катионные каналы могут способствовать как выходу калия, так и входу натрия, поскольку большая часть этих каналов не обладает высокой селективностью к калию по сравнению с натриевой 14, 15). Дополнительный источник входящего в клетку натрия — это натрий—зависимые вторичные активные транспортные системы (глава 4). Наконец, потенциал—чувствительные натриевые каналы также вносят свой вклад в натриевую проводимость в покое, поскольку эта проводимость блокируется тетродотоксином, хотя и в небольшой степени 9).
Хлорные каналы семейства CLC (глава 3) широко распространены в нервных и мышечных клетках. Наличие хлорных каналов обеспечивает стабилизацию мембранного потенциала (см. ниже). Эти каналы также участвуют в установлении внутриклеточной концентрации хлора, взаимодействуя с системами хлорного транспорта 16, 17). При низком уровне экспрессии каналов CLC, например, в нейронах эмбрионального гиппокампа, значение ЕClменее отрицательно по сравнению с потенциалом покоя, благодаря вкладу активного транспорта ионов хлора внутрь клетки и их накоплению в цитоплазме. В нейронах взрослого животного экспрессия каналов CLC более выражена, и мембранная проводимость для хлора выше, поэтому накопление внутриклеточного хлора невозможно, и ЕСl равен мембранному потенциалу. В клетках центральной нервной системы до 10% проводимости мембраны при потенциале покоя обеспечивается за счет хлорных каналов 18).
§3. Изменения мембранного потенциала
Необходимо помнить, что, обсуждая потенциал покоя, мы всегда говорим о состоянии равновесия. Например, выше было сказано, что изменение внеклеточной концентрации хлора не оказывает значительного влияния на мембранный потенциал, потому что внутриклеточная концентрация при этом подстраивается под новые условия. В конце концов это действительно происходит, но процесс занимает какое-то время, и в течение этого времени изменение внеклеточного уровня хлора оказывает влияние на мембранный потенциал.
Равновесный мембранный потенциал представляет собой тот фоновый уровень, на котором происходят все изменения мембранного потенциала. Как они происходят? Обычно кратковременные изменения мембранного потенциала (подобные тем, которые наблюдаются при взаимодействии нейронов между собой) происходят за счет временных изменений проницаемости мембраны. Как мы знаем из уравнения постоянного поля, увеличение натриевой проницаемости (также как и снижение калиевой) приводит к деполяризации, то есть к смещению мембранного потенциала в сторону натриевого равновесного потенциала. Напротив, увеличение калиевой проницаемости вызывает гиперполяризацию. Еше один важный для сигнальных процессов клетки ион — это кальций. Внутриклеточная концентрация кальция очень низка (глава 4), а ЕСа в большинстве клеток превышает +150 мВ. Следовательно, увеличение кальциевой проницаемости должно приводить к входу кальция в клетку и деполяризации мембраны.
Особый интерес представляет влияние хлорной проницаемости на мембранный потенциал. Как было отмечено выше, хлор вносит незначительный вклад в потенциал покоя. Внутриклеточная концентрация хлора подстраивается под новые условия за счет работы существующих хлорных транспортных механизмов. Влияние кратковременного увеличе-
100 Раздел II. Передача информации в нервной системе
ния хлорной проницаемости может выражаться как в гиперполяризации, так и в деполяризации, в зависимости от того, положителен или отрицателен ЕС1по отношению к потенциалу покоя. Это, в свою очередь, зависит от работы транспортного механизма, либо наполняющего клетку хлором, либо выводящего его наружу. В любом случае, влияние хлора на мембранный потенциал обычно невелико. Тем не менее, увеличение хлорной проницаемости может иметь важное значение для регулирования сигнальных процессов, поскольку оно поддерживает мембранный потенциал в диапазоне ЕClи за счет этого ослабляет способность других процессов изменить мембранный потенциал.
Поддержание мембранного потенциала на неизменном уровне играет важную роль в регуляции возбудимости таких клеток, как скелетная мышца, хлорная проводимость которой в покое достаточно велика. В таких клетках кратковременный вход положительных ионов вызовет меньшую деполяризацию в присутствии хлорной проницаемости, нежели в ее отсутствии, поскольку их вход отчасти балансируется входом хлора через уже открытые каналы. Мутации хлорных каналов, снижающие хлорную проницаемость мембраны, приводят к некоторым мышечным заболеваниям. Потерявшие нормальную высокую хлорную проводимость мышцы находятся в состоянии повышенной возбудимости (myotonic) 19, 20).
Выводы
∙ Нервные клетки обладают высокой внутриклеточной концентрацией калия и низкой концентрацией натрия и хлора, так что калий стремится выйти из клетки, а натрий и хлор стремятся войти в нее. Стремлению калия и хлора проникнуть через мембрану в направлении концентрационного градиента противостоит мембранный потенциал.
∙ В модели идеальной клетки, обладающей только калиевой и натриевой проводи-
мостями, мембранный потенциал может в точности уравновесить концентрационные градиенты таким образом, чтобы суммарный ток обоих ионов равнялся нулю. В этом случае мембранный потенциал соответствует равновесному потенциалу для калия и хлора.
∙ Изменение внеклеточного уровня калия приводит к изменению его равновесного потенциала и, следовательно, мембранного потенциала. Напротив, изменение внеклеточной концентрации хлора приводит в конечном итоге к изменению его внутриклеточного уровня, так что сдвиг хлорного равновесного потенциала и мембранного потенциала от своих первоначальных значений носит кратковременный характер.
∙ Мембрана реальных клеток обладает также натриевой проводимостью. В результате в состоянии покоя происходит постоянная диффузия натрия внутрь, а калия наружу клетки. Эти токи в точности уравновешиваются активным ионным транспортным механизмом — натрий-калиевым насосом, работающим по схеме 3 иона натрия к 2 ионам калия. В этих условиях, величина мембранного потенциала зависит от натриевого и калиевого равновесных потенциалов, относительных проводимостей для этих ионов, а также от соотношения ионов в цикле насоса.
∙ Благодаря тому, что натрий-калиевый насос переносит больше положительных ионов наружу, чем внутрь клетки, он вносит непосредственный вклад в мембранный потенциал в размере нескольких мВ.
∙ В зависимости от особенностей хлорных транспортных механизмов, равновесный потенциал для хлора может быть как более, так и менее отрицательным по отношению к потенциалу покоя. Несмотря на незначительное влияние распределения хлора на потенциал покоя, наличие высокой хлорной проводимости необходимо для поддержания электрической стабильности клетки.
Рекомендуемая литература
о Hodgkin, A. L., and Katz, В. 1949. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 108: 37-77. (The constant field equation is derived in Appendix A of ihis paper.)
Глава 5. Ионные механизмы потенциала покоя 101
о Junge, D. 1992. Nerve and Muscle Excitation, 3rd Ed. Smaller Associates, Sunderland, MA, Chapters 1-3.
о Mullins, L.J., and Noda, K. 1963. The influence of sodium-free solutions on membrane potential of frog muscle fibers. J. Gen. Physiol. 47: 117-132.
Цитированная литература
1. Bernstein, J. 1902. Pflugers Arch. 92: 521-562.
2. Young, J.Z. 1936. Q.J. Microsc. Sci. 78: 367-386.
3. Hodgkin, A. L. 1973. Proc. R. Soc. Land. В 183: 1-19.
4. Goldman, D. E. 1943. J.Gen. Physiol. 27: 37-60.
5. Hodgkin, A.L., and Katz, R 1949. J. Physiol. 108: 37-77.
6. Mullins, L. J., and Noda, K. 1963. J. Gen. Physiol. 47: 117-132.
7. Matthews, G., and Wickelgren, W. O. 1979. J. Physiol. 293:393-414, Appendix (by A. R. Martin).
8. Fan, P., and Katz, B. 1951. J. Physiol. 115: 320-370.
9. Nicholls, J.G., and Baylor, D.A. 1968. J. Neuro-physiol. 31:740-756.
10. Baylor, D. A., and Fuortes, M. G. F. 1970. J. Physiol. 207: 77-92.
11. Martin, A. R., and Levinson, S. R. 1985. Muscle Nerve 8: 354-362.
12. Edwards, C. 1982. Neuroscience 7: 1335-1366.
13. Hille, B. 1992. Ionic Channels of Excitable Membranes, 2nd Ed. Sinauer Associates, Sunderland, MA, p. 352.
14. Yellen, G. 1982. Nature 296: 357-359.
15. Chua, M., and Betz, W.J. 1991. Biophys. J. 59: 1251-1260.
16. Staley, K., et al. 1996. Neuron 17: 543-551.
17. Mladinic, M., et al. 1999. Proc. A Soc. Land. В 266: 1207-1213.
18. Gold, M. R., and Martin, A. R. 1983. J. Physiol. 342:99-117.
19. Barchi, R. L. 1997. Neurobiol. Dis. 4: 254-264.
20. Cannon, S.C. 1996. Trends Neurosci. 19: 3-10.