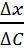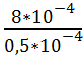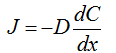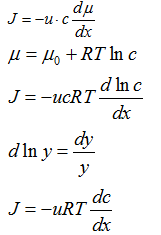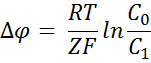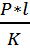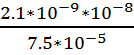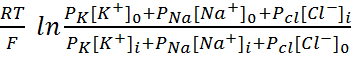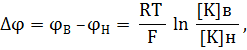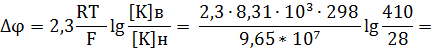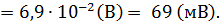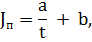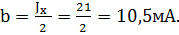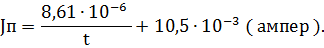Основы биофизики
Задача 1
Чему равна плотность потока формамида через
плазматическую мембрану Chara
ceratophylla толщиной 8 нм,
если коэффициент диффузии его составляет 1,4*10-8 см2 * с-1, концентрация
формамида в начальный момент времени снаружи была равна 2 * 10-4 М (моль/литр),
внутри в 10 раз меньше
Дано:
x = 8 нм = 8 * 10-9
м = 8 * 10-7 см
D = 1,4*10-8 см2 *
с-1
С0 = 2 * 10-4 М
Сi
= 2 * 10-5 М
Найти: J
Решение:
Воспользуемся уравнением Фика
J = — D
Jdx = — DdC
Продифференцируем левую и правую
части:
J= -D
В итоге получаем:
J = 1.4* 10-8
* 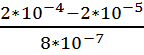
М*см/с
Задача 2
Бислойная липидная мембрана (БЛМ)
толщиной 10 нм разделяет камеру на две части. Плотность потока метиленового
синего через БЛМ постоянна и равна 3 * 10-4 М * см/с, причем концентрация его с
одной стороны мембраны составляет 10-2 М, а с другой 2 * 10-3 М. чему равен
коэффициент диффузии этого вещества через БЛМ?
Дано:
x = 10 нм =
10 * 10-9 м = 10-6 см
J = 3 *10-4 М
* см/с
С0 = 10-2 М
Сi = 3 * 10-3
М
Найти: D
Решение:
Воспользуемся уравнением Фика
J = — D
Очевидно, что в нашем случае можно
записать
J = — D
Тогда,
D = -J
D = — 3 *
10-4 * 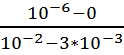
10-8 см2 * с-1
Задача 3
Найти коэффициент проницаемости
плазматической мембраны Mycoplasma для
формамида, если при разнице концентраций этого вещества внутри и снаружи
мембраны, равной 5 * 10-4 М, плотность потока через мембрану — 8 * 10-4М *см/с.
Дано:
J = 8 * 10-4
М * см/с
Найти: Р
Решение:
Воспользуемся формулой:
Р = К* (1)
где К — коэффициент распределения
вещества
х — толщина мембраны
Толщину мембраны можно найти из
уравнения Фике:
J = — D
x = — D
подставим его в первое уравнение:
Р = К* = К*
В итоге получаем, принимая К = 1: Р
= К* = 16 см/с
Задача 4
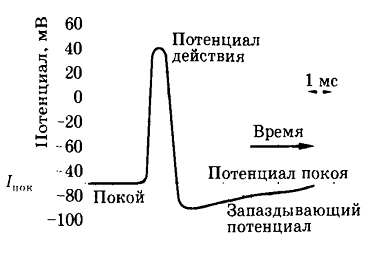
Потенциал покоя нервного волокна
кальмара равен — 60 мВ а потенциал действия +35мВ.
Вследствие чего происходит такое
изменение мембранного потенциала?
Ответ:
Все живые клетки при действии
различных раздражителей переходят в возбужденное сост. При возбуждении разность
потенциалов между клеткой и окружающей средой изменяется. Появляется
электрический импульс.
Потенциал действия — разность
потенциалов между цитоплазмой и окружающей средой при возбуждении.
Распространение импульса определяется изменением состояния мембраны. В
состоянии покоя в результате активного транспорта, значение концентрации ионов
калия K+ выше в
мембране, чем в окружающей среде. Для ионов натрия все Na+ наоборот.
При этом на внутренней поверхности мембраны будет отрицательный «-» заряд, в
рассматриваемом варианте он равен — 60 мВ. При возбуждении будет происходить
следующее:
. Вначале увеличивается
проницаемость мембраны для ионов натрия Na+.
Натривевые каналы открываются лишь при возбуждении. Ионы Na+ входят в
мембрану, в результате чего внутренняя поверхностьть мембраны меняет свой заряд
с «-« на «+», т.е. происходит деполяризация мембран. Натриевый канал открыт
малое время и в течении этого времени происходит изменение мембранного
потенциала до +35мВ.
. Во время генерации импульса
натриевый канал закрывается и открывается калиевый канал. Ионы K+ выходят
наружу, что приводит к восстановлению — заряда на внутренней стороне мембраны.
Во время импульса проницаемость мембраны увеличивается более чем в 5000 раз.
. Наступает реполяризация. Это
приводит к возникновению потенциалов действия на соседних невозбужденных
участках. Вновь возбужденный участок в свою очередь вновь становится
электроотрицательным, а возникающий локальный ток возбуждает следующий участок
и т. д.
Все эти процессы можно представить
на графике
Задача 5
Показать, что уравнение Фика для
диффузии является частным случаем уравнения Теорелла
Ответ:
Скорость диффузии подчиняется
важному феноменологическому закону, который называется I законом Фика:
Поток равен числу частиц,
диффундирующих вдоль оси Х в единицу времени через единичную площадку,
перпендикулярную это оси.
Поток прямо пропорционален
коэффициенту диффузии и градиенту концентрации dС/dх в данной точке оси х в
данный момент времени.
Чисто феноменологически первый закон
Фика можно рассматривать как некий частный случай общей формулы теоремы для
потока:
движущая сила,×
Концентрация ×Поток =
Подвижность
где поток есть количество вещества в
молях, которое проходит в единицу времени через единичную площадку,
перпендикулярно направлению движения.
Обозначив uRT = D , получим I закон
диффузии Фика
Задача 6
Определить равновесный мембранный
потенциал, создаваемый на бислойной липидной мембране ионами калия (К+) при
температуре 200С, если концентрация калия с одной стороны мембраны равна 10-3
М, а с другой — 10-5М
Дано:
С0 = 10-3 М
С1 = 10-5 М
Т = 200С = 293 К
Найти:
Решение:
По уравнению Нернста:
где R —
универсальная газовая постоянная (8,31 Дж/моль*К)
F —
постоянная Фарадея (9,652*107 Кл*кг/моль)
Z — заряд иона
(для К+ = 1)
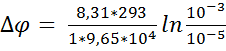
Задача 7
Рассчитать потенциал покоя
гигантского аксона кальмара, если известно, что концентрация ионов натрия
снаружи равна 440 мМ, а внутри — 49 мМ. Температура равна 200С.
Дано:
С0 = 440 мМ
С1 = 49 мМ
Т = 200С = 293 К
Найти:
Решение:
По уравнению Нернста:
где R —
универсальная газовая постоянная (8,31 Дж/моль*К)
F —
постоянная Фарадея (9,652*107 Кл*кг/моль)
Z — заряд
иона (для Na+ = 1)
= 0,025226 * 2.195 = 55.371 мВ
Задача 8
Потенциал покоя нерва конического
краба равен 89 мВ.
Чему равна концентрация ионов калия
внутри нерва, если снаружи она составляет 12 мМ?
Принять температуру равной 200С.
Дано:
= 89 мВ = 89 * 10-3 B
С1 = 12 мМ = 12 * 10-3 M
Т = 200С = 293 К
Найти: С0
Решение:
По уравнению Нернста:
где R —
универсальная газовая постоянная (8,31 Дж/моль*К)
F —
постоянная Фарадея (9,652*107 Кл*кг/моль)
Z — заряд
иона (для К+ = 1)
=
— lnC1 =
=
+ lnC1= exp{
+ lnC1}= exp{
= exp{3.527 + (-4.423)} =
exp{-0.896}= 0.408 M410 мМ
Задача 9
Найти плотность потока (в начальный
момент времени), коэффициент диффузии глицерина через мембраны одноклеточных
водорослей, если глицерин в начальный момент времени введен в водный раствор,
содержащий клетки, в концентрации C0 = 2 * 10-5
М (моль/литр) и эта концентрация поддерживается постоянной.
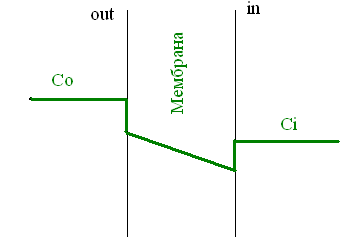
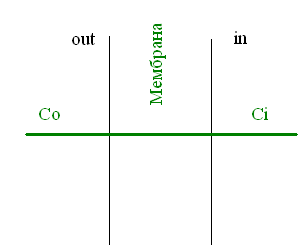
Изобразить графически распределение
глицерина внутри клетки, в мембране и в окружающей среде:
А) в начальный момент времени;
Б) в некоторый промежуточный момент
времени;
В) в установившемся равновесном
состоянии.
Коэффициент проницаемости через
мембрану для глицерина Р = 2,1 * 10-9 м/с, коэффициент распределения вещества
между мембраной и водной средой К = 7,5 * 10-5. Толщина мембраны l = 10 нм.
Дано:
C0 = 2 * 10-5
моль/л = 2 * 10-5 моль/см3 = 2 * 10-2 моль/м3
Р = 2,1 * 10-9 м/с
К = 7,5 * 10-5.
l = 10 нм. =
10-8 м
Найти: J, D
Решение
Для нахождения плотности потока
используем формулу:
J = P(C0 — C1)
Учтем то, что в начальный момент
времени С1 = 0, тогда
J = P*C0
J = 2,1 *
10-9 *2 * 10-2 = 4,2 * 10-11 моль/м2*с
Коэффициент диффузии находим из
выражения:
D =
D = 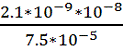
Строим графики:
А) в начальный момент времени
Б) в некоторый промежуточный момент
времени
В) в установившемся равновесном
состоянии.
Задача 10
Среднее значение концентрации ионов
калия, натрия и хлора в аксоплазме гигантского аксона кальмара равны
соответственно 410, 49, 40 моль/л (М). В морской воде концентрация этих же
ионов равна соответственно 10, 460, 540 моль/м3 (М).
Вычислить потенциал Нернста для
каждого из этих ионов при 270С
Дано:
Калий:
С0 [K+] = 10 М
С1 [K+]= 410 М
Натрий:
С0 [Na+] = 460 М
С1 [Na+]= 49 М
Хлор;
С0 [Сl-] = 540 М
С1 [Cl-]= 40 М
Т = 270С = 300 К
Найти:
Решение:
По уравнению Нернста:
где R —
универсальная газовая постоянная (8,31 Дж/моль*К)
F —
постоянная Фарадея (9,652*107 Кл*кг/моль)
Z — заряд
иона (для К+ = 1; для Na+ = 1; для Cl-1 = -1)
Для калия:
= 0,0258 * (- 3,713) = — 0,0959 В
96 мВ
Для натрия:
= 0,0258 * 2,24 = 0,05785 В
58 мВ
Для хлора:
= -0,0258 * 2,6 = — 0,06724 В
— 67 мВ
Найдем общий мембранный потенциал
для заданной аксоплазме гигантского аксона кальмара .
Уравнение Нернста — это частный
случай уравнения Гольдмана, которое превращается в первое , если проницаемость
для одного из ионов гораздо выше, чем для других.
Воспользуемся уравнением Гольдмана:
Мембранный потенциал
формамид
плазматический мембрана
Например, в гигантском аксоне
кальмара P — проницаемости: Na : Cl = 1 : 0,04 : 0,45, т. е. проницаемость для
К+ заметно выше, чем для других ионов.
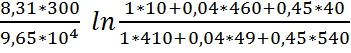
= 0,02583 *
ln 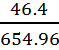
мВ
Литература
1. Волькенштейн
М.В. Биофизика. М.: Наука, 1988.
2. Рубин
А.Б. Биофизика: В 2 т. М.: Высшая школа, 2000.
. Кантор
Ч., Шиммел П. Биофизическая химия: В 3 т. М.: Мир, 1984.
. Блюменфельд
Л.А. Проблемы биологической физики. М., 1977.
. Ивков
В.Г., Берестовокий Г.Н. Липидный бислой биологических мембран. М., 1982.
. Конев
С.В., Волотовский И.Д. Фотобиология. Минск, 1979.
. Котык
А., Яначек К. Мембранный транспорт. М., 1980.
. Ходжкин
А. Нервный импульс. М., 1965.
. Давид
Р. Введение в биофизику. М.: Мир, 1982.
ЗАДАЧА №1
Вычислить величины потенциалов покоя, клеток гигантского аксона кальмара в верхних слоях океана, где температура 25 оС, и в глубине, где температура 6 оС. Концентрация ионов калия в аксоне 410 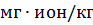
Решение: Величина мембранного потенциала клетки определяется разностью потенциалов между внутриклеточной и наружной по отношению к клетке средами. При соблюдении равновесия Доннана имеет место соотношение:
где [K]в и [K]н – соответственно концентрация калия внутри и снаружи клетки, R- универсальная газовая постоянная, F- число Фарадея.
Поскольку натуральный и десятичный логарифмы связаны соотношением: 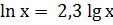
Аналогично можно вычислить, что ∆φ2=64,5 мВ.
Ответ: величина потенциала покоя в аксоне кальмара в верхних слоях океан 19 (мВ), а в глубине 64,5 (мВ).
ЗАДАЧА № 2
Электроды, наложенные на середину холки коровы, соединены с генератором прямоугольных импульсов (это означает, что создаваемое генератором напряжение резко возрастает до определенного значения, затем остается постоянным заданное время, по прошествии которого снова падает до нуля). Исследование пороговых реакций коровы показало, что величина хронаксии равна 0,82 мс и соответствующее ей значение раздражающего тока равно 21 мА. На основе этих данных написать выражение, дающее связь между величиной порогового тока и временем его действия.
Решение: Зависимость величины порогового тока от времени его действия дается законом Вейсса:
где b – реобаза, т. е минимальная сила порогового тока при длительном его действии. Время τ, необходимое для раздражения при силе тока, равной двум реобазами, называется хронаксией. Отсюда следует, что сила тока при хронаксии Jx =2 b. Это дает возможность вычислить значение константы b;
Для нахождения константы Вейсса а подставим в уравнение Вейсса значения Jx и b:
Отсюда 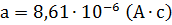
Таким образом, зависимость порогового тока от времени его действия будет выражена уравнением:
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности… |
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями… |
Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм… |
Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени… |
|
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены: ПУНКЦИЯ И КАТЕТЕРИЗАЦИЯ ПОДКЛЮЧИЧНОЙ ВЕНЫ Ситуация 26. ПРОВЕРЕНО МИНЗДРАВОМ |
73,2% бесплатных материалов
958 руб. средняя цена курсовой работы
350 руб. средняя цена домашнего задания
116 руб. средняя цена решённой задачи
157 руб. средняя цена лабораторной работы
170 руб. средняя цена реферата
171 руб. средняя цена доклада
1654 руб. средняя цена ВКР
657 руб. средняя цена диссертации
607 руб. средняя цена НИР
362 руб. средняя цена отчёта по практике
281 руб. средняя цена ответов (шпаргалок)
200 руб. средняя цена лекций
220 руб. средняя цена семинаров
283 руб. средняя цена рабочей тетради
178 руб. средняя цена презентации
67 руб. средняя цена перевода
138 руб. средняя цена изложения
149 руб. средняя цена сочинения
314 руб. средняя цена статьи
Гарантия возврата средств
Преподаватель который помогает студентам и школьникам в учёбе.
Вычислить величины потенциалов покоя, клеток гигантского аксона кальмара в верхних слоях океана
 |
 |
Физика |
 |
 |
Решение задачи |
 |
 |
18 февраля 2021 |
 |
 |
Выполнен, номер заказа №16684 |
 |
 |
Прошла проверку преподавателем МГУ |
 |
 |
245 руб. |
Напишите мне в чат, пришлите ссылку на эту страницу в чат, оплатите и получите файл!
Закажите у меня новую работу, просто написав мне в чат!
Описание заказа и 38% решения ( + фото):
Вычислить величины потенциалов покоя, клеток гигантского аксона кальмара в верхних слоях океана, где температура 25 оС, и в глубине, где температура 6 оС. Концентрация ионов калия в аксоне 410 мг ∙ ион/кг, а концентрация ионов калия вне аксона 28 мг* ион / кг. Дано: [K]н= 28 мг ∙ ион/кг [K]в=410 мг ∙ ион/кг t1= 25 оС, T1= 298 K t2= 6 оС, T2=279 K ∆φ1=? ∆φ2=?
Решение: Величина мембранного потенциала клетки определяется разностью потенциалов между внутриклеточной и наружной по отношению к клетке средами. При соблюдении равновесия Доннана имеет место соотношение: , где – соответственно концентрация калия внутри и снаружи клетки, — универсальная газовая постоянная, — число Фарадея. Поскольку натуральный и десятичный логарифмы связаны соотношением: . Аналогично можно вычислить, что . Ответ: величина потенциала покоя в аксоне кальмара в верхних слоях океан , а в глубине
Похожие готовые решения по физике:
- Электроды, наложенные на середину холки коровы, соединены с генератором прямоугольных импульсов
- Для регистрации переменных импульсных сигналов, создаваемых некоторыми рыбами, измерительный прибор
- Сопротивление образца мышечной ткани животного измеряется при пропускании через него сначала постоянного
- Ультрафиолетовая лампа ЛЭ-30, применяемая в животноводстве и ветеринарии, создает световой поток
- Какое количество эфира, находящегося при температуре кипения, должно испариться
- Потенциал действия в гигантском аксоне кальмара обусловлен переносом 100 пг натрия из внеклеточной среды
- Аппарат для гальванизации АГН -5 создает плотность тока 0,12 мА/см2 . Какое количество электричества
- Средняя мощность разряда электрического сома примерно 8 Вт при напряжении 360 В. Время
- Какая часть молекул водорода при температуре 40° С обладает скоростями от 700 до 720 м/с? Молярная масса водорода 2 г/моль.
- Средняя мощность разряда электрического сома примерно 8 Вт при напряжении 360 В. Время
- Для регистрации переменных импульсных сигналов, создаваемых некоторыми рыбами, измерительный прибор
- Электроды, наложенные на середину холки коровы, соединены с генератором прямоугольных импульсов