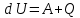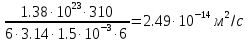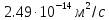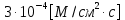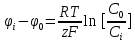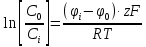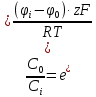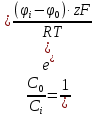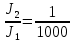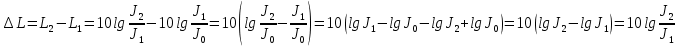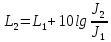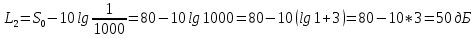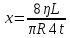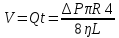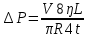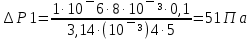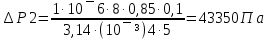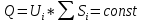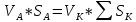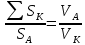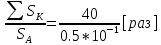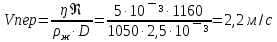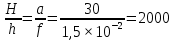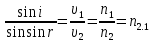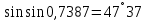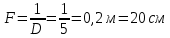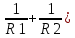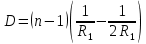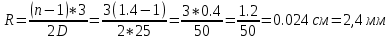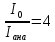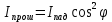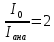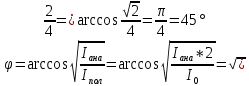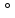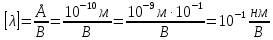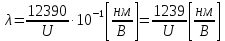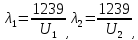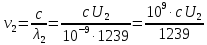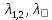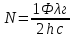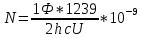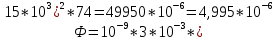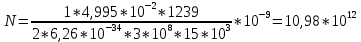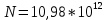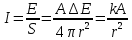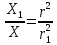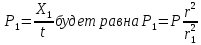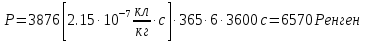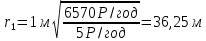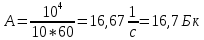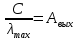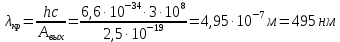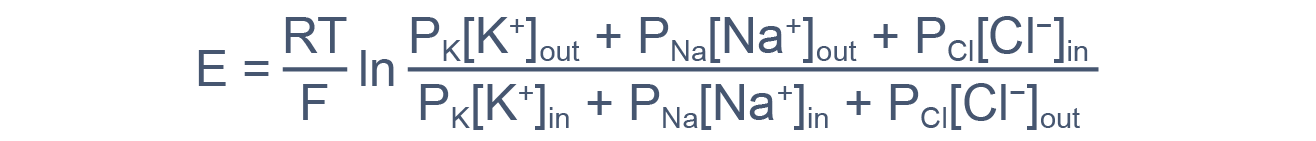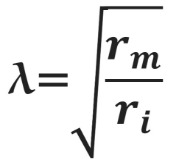Подборка по базе: Судебное решение для курсовой.docx, ПР№1 Решение.docx, 1 Планируемые изменения инфраструктуры.docx, Дело 12-0272_2021. Решение по жалобе_протесту на постановление (, Квадратные уравнения. Решение неполных кв.ур..ppt, !!! готовое решение задач с формулами.doc, Бухгалтерский баланс ЗАО Стэк и решение.docx, Готовое решение_ Как произвести увольнение работника по медицинс, ОБОБЩЕНИЕ ПО ТЕМЕ Изменения с вещвами.docx, раздаточный материал к уроку решение задач на дроби.docx
1.Термодинамической системе было передано тепло в количестве 140 Дж, а также над ней была совершена работа в 65 Дж. Как изменилась внутренняя энергия системы в этом процессе?
Дано: Q=140 Дж. A=65 Дж. Найти: dU=?
Решение: Запишем формулу изменения внутренней энергии:
Где A — работа совершенная над газом (Работа внешних сил), Q — кол-во теплоты, переданное данной системе. Осталось посчитать:
dU=140+65=205 Дж=0.205кДж.
Ответ: dU=0.205кДж
2. Определите калорический коэффициент кислорода при окислении глюкозы, если из экспериментов с калориметрической бомбой известно, что при окислении 1 г глюкозы выделяется 15,7 кДж теплоты.
Задача 3. Сколько полезной работы может быть получено при сжигании 12*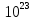
Дано: V = 12*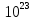
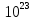
Найти- А (полезную)
Решение: Теплота сгорание глюкозы Q=2800 кДж/моль. согласно справочнику
КПД (n) = A Q *100%
Na=Число Авогадро 6,022*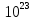
Q- Количество теплоты полученное рабочим телом от нагревателя
А — полезная работа, совершаемая рабочим телом за цикл
Тогда A=nQV=0,5*2800*2=2800 кДж.
Ответ: 2800 кДж.
4. Спортсмен, пробегая дистанцию, выделяет за 1 мин 90 л воздуха, в котором содержится
12% кислорода и 8% углекислого газа. Каков расход энергии спортсмена за 5 мин
дистанции?
Дано: t1=1час, V=90л, VO2=12%, VCO2=8%, t2=5 мин
Найти: E-?
Решение: В 100мл 21% O2 и 0,003 CO2
Расход O2 на 100мл VO2= 21-12=9%=9мл O2
Расход CO2 на 100мл VCO2=8%=8мл CO2
ДК-дыхательный коэффициент ДК= VCO2/ VO2=8/9=0,88
КК-калорический коэффициент ДК=0,88=КК=20,515 кДЖ
В 100мл – 9 мл В 90000мл- Хмл
Х=90000 х 9/100= 8100мл
За 1 минуту 1000 мл – 20,515кДЖ
8100мл- Х
Х= 20,515 х 8100/1000=166кДЖ
За 5 минут Е=166кДЖ х 5= 830кДЖ
Ответ: Е= 830 кДЖ
5. Удельная электрическая емкость мембраны аксона, измеренная внутриклеточным микроэлектродом, оказалась равной 0,5 мкФ/см^2. По формуле плоского конденсатора оценить толщину гидрофобного слоя мембраны с диэлектрической проницаемостью равной 2.
Дано: C=0,5 мкФ/см^2 E=2
Найти: h-?
Решение: C=Eo*E*S/h-выражение для емкости плоского конденсатора, где С-емкость
Е-относительная диэлектрическая проницаемость
Ео=8,85*10^-12 Ф/м-диэлектрическая постоянная
S-площадь обкладки конденсатора (мембраны аксона)
h-толщина гидрофобного слоя мембраны
Cуд.=C/S=0,5*10^-6/(10^-2 м)^2=0,5*10^-2 Ф/м^2
Е=Ео/Е>1
выражаем h:
h=EoES/C=EoE/Cуд.= 2*8,85*10^-12/0,5*10^-2=35,4*10^-10=3,5 Нм
Ответ: 3,5 Нм
6. Используя уравнение Эйнштейна Sкв = 2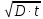
диффузии, определите, какое расстояние на поверхности мембраны эритроцита проходит
молекула фосфолипида за 1 секунду в результате латеральной диффузии? D принять равным 10-
12 м^2с.Сравните с окружностью эритроцита диаметром 8 мкм.
Дано: 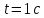
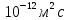
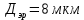
Решение:
Sкв = 2
Sкв=2 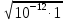
l) (длина окружности)=2ПR=2Пd (п-число пи, d-диаметр
1секунда=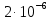
x =3.14*8
решаем пропорцию
x=(3,14*8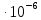
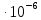
x=12,28 с Ответ: 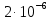
7. Микровязкость мембраны эритроцита при температуре 37С равна 6 Пз. Найти величину коэффициента диффузии для ионов кальция. Если радиус негидратированного иона кальция 1,5 нм.
Дано: Т=37С, n=6 Пз, r=1,5 нм, k(постоянная Больцмана)=1, 38х10^-23Дж/К, число пи=3,14
Найти: D=? – величину коэффициента диффузии
Решение:
1.) Т=37С=310К, n(микровязкость)=6 Пз, k(постоянная Больцмана)=1, 38х10^-23Дж/К, r(радиус)=1,5нм, пи(число)=3,14.
3.) Найдем искомое по формуле: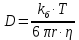
Ответ: D=
8. Бислойная липидная мембрана (БЛМ) толщиной 10 нм разделяет камеру на две части. Плотность потока метиленового синего через БЛМ постоянна и равна 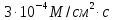
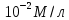
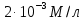
Дано: h = 10 нм = 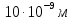
С0 = 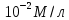
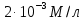
Найти: D-?
Решение:
Воспользуемся уравнением Фика:
J = — D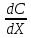
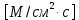
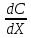
D=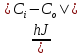
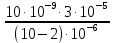
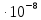
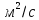
Ответ: 3.75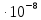
9. Концентрация глюкозы в клетке равна 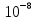
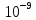
Дано:
[Гл]i=10-8 моль/л [Гл]o=10-9 моль/л T=20о C=293К N=10 моль
Найти: Δµ (в клетку) Δµ (из клетки)
Решение: µ=µ0+RT*lnC
µ-химический потенциал, Дж/моль µо-стандартный химический потенциал, Дж/моль
R=8,3 – газовая константа, (Дж/(моль*К) T(к)-температура С [число молей]-концентрация
В клетку: Δµ=µо-µi=µ0o+RT*lnCo-µ0i + RT*lnCi=RT*ln(Co/Ci)=8,3*293*ln(10-9/10-8)=-2432*2,3lg10=-5594 [Дж/моль]
-5,6 [кДж/моль] < 0 (Пассивная диффузия)
Из клетки: Δµ=µi— µо= µ0i+RT*lnCi — µ0o+RT*lnCo=8,3*293*ln(10-9/10-8)=2432*2,3lg10=5594 Дж/моль5,6 кДж/моль>0 (Только активный транспорт)
10. Найти приращение электрохимического потенциала при транспорте кальция из клетки и в клетку, если концентрация кальция в клетке равна 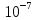
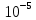
Дано: Ci(Ca)=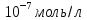
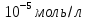
T=20C=293K L(фи)=(-60)мВ
Найти:
u1-? u2-?
Решение: u=R•T•ln•(-Co/Ci) +ZF(Lo+L1)
u- химический потенциал
R=8,3 [Дж/моль•К] газовая постоянная
F= постоянная Фарадея
Z= 2 валентность ионов
Со=внеклеточная концентрация иона
Сi= внутриклеточная концентрация иона
M=Mo+R•T•ln 10-5/10-7 + 2•9,6 •60= 8,3•293• ln 10^2 +2•9,6•60=11186,74+1152=
12338,7 Дж/моль=12,3 КДж/моль.
11. Концентрация ионов натрия в клетке 1 ммоль/л, вне клетки 180 ммоль/л. Разность потенциалов на мембране (- 80 мВ). Можно ли осуществить активный транспорт ионов натрия при помощи натрий-калиевого насоса из клетки на наружную поверхность мембраны, при температуре 37 С, изменение свободной энергии при гидролизе 1 моль АТФ = (- 45) кДж/моль, КПД насоса 50%.
Дано: {Na}i= 1мМ {Na}o=180 мМ t=37
Разность потенциалов 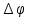
12. Концентрация глюкозы в плазме крови 3,5 мМ/л, концентрация глюкозы в
эритроците 5 мМ/л. Концентрация ионов Na+ в эритроците 4 мМ/л, а в плазме 140
мМ/л, температура 37С. Можно ли транспортировать молекулу глюкозы в
эритроцит, используя вторичный активный транспорт. Разность потенциалов на
мембране эритроцита (-60) мВ.
13. Какое количество одновалентных ионов нужно переместить на наружную поверхность мембраны из клетки, чтобы сохдать потенциал покоя 120мВ? Площадь поверхности мембраны 10-9 м2, удельная электроёмкость мембраны Суд=10-2 Ф/м2.
Дано: 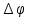
Решение:
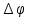
1. С=Суд*S=10-2*10-9=10-11Ф — электроёмкость мембраны.
2. Заряд поверхности мембраны находим через ёмкость: q=C*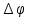
3. Число ионов, образующих такой заряд, рано n=q/e=10-12/1,6*10-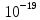
Ответ: n=6,2*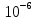
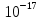
14. Найдите, какой должна быть концентрация ионов калия в клетке, при которой
величина равновесного калиевого потенциала равна (-100) мВ, при температуре 37оС,
[K+]o = 6х10-3 моль/л
Дано:
Найти: Сi — ?
Решение:
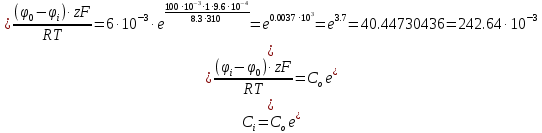
15. Определите равновесный мембранный потенциал при отношении концентраций
натрия снаружи и внутри а) 1:1; б) 10:1; в) 100:1, температура Т = 310 К
Дано:
[Na+]o/[Na+]i=1/1
[Na+]o/[Na+]i=10/1
[Na+]o/[Na+]i=100/1
T=37°C
Найти:
Дельта фи
Решение:
(Фи) yi-yo=RT/ZF•ln[Na+]o/[Na+]i
R- 8,3 [дж/моль•К°] газовая константа
T[К°]- температура
Z[1]- валентность иона
F- 9,6•10^4 [кл/моль]
yi-yo- равновесный потенциал [B]
RT/ZF=8,3•310/1•9,6•10^4=268•10^4=268•10^1•10^-3=27[мВ]
а)yi-yo=27ln1/1=0 [мВ]
б)yi-yo=27ln10/1=27•2,3lg10=62 [мВ]
в)yi-yo=27ln100/1=27•2,3lg10^2=124 [мВ]
16. Чему равна напряженность электрического поля на мембране в состоянии покоя,
если концентрация ионов калия внутри клетки 125 ммоль/л, снаружи – 2,5 ммоль/л, а
толщина мембраны 8 нм?
Дано:[К+]i=125 ммоль/л [К+]о=2,5 ммоль/л
h=8 нм=8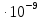
Найти: Е-?
Решение:
Е= — (Фi-Фо)/h
Фi-Фо=RT/ZF * ln(Co/Ci)
Фi-Фо= ((8,31*310)/(1*96485)) * ln ((2.5*10^-3)/(125*10^-3))=-0,105 Вольт
Е= (0,105/8*10^-9)= 0,013 *10^-9 В/м
*Пояснения*
Е — напряжённость эл.поля
Фi-Фо разность потенциалов
h — толщина мембраны
R- газовая постоянная(8,31дж/моль*К)
Т — температура (310 К)
С- концентрация
17. Определите равновесный мембранный потенциал митохондрий, если при 37 ͦС внутри митохондрий pH=9, а в окружающей среде рН=7.
Дано: T=37°C = 310 K
pH(i) = 9 pH(o)= 7
Найти:
∆(фи)=?
Решение:
Равновесный мембранный потенциал можно рассчитать с помощью формулы Нернста:
1) ∆(фи) = (фи i) — (фи o) = RT/ZF * Ln C(o)/C(i),
где (фи i) — потенциал на внутренней части мембраны, (фи o) — потенциал на внешней части мембраны, R — газовая постоянная, Т-температура, Z- валентность ионов, F — постоянная Фарадея, Со-концентрация ионов снаружи клетки, Сi- концентрация ионов внутри клетки.
Водородный показатель рН определяется как
2) рН=-lg[H^+],
где величина [Н^+] имеет размерность моль/л и по своей сути является концентрацией. Вычислим концентрацию протонов (ядер атомов водорода) по величине рН:
3) C=[H^+]=10^-pH.
Тогда объединение (1) — (3) позволяет записать:
4) ∆(фи) =RT/ZF * ln * 10^-pHo / 10^-pHi ==RT/ZF * ln * 10^pHo / 10^pHi =RT/ZF * ln * 10^(pHi — pHo) = RT/ZF*(pHi — pHo) * ln10
Подставим числа в выражение (4) :
∆(фи) =(8.31 Дж/моль*К * 310 К / 1*96500Кл/моль ) *(9-7) ln10=0,123 Дж/К =123мВ
Ответ: ∆(фи) = 123 мВ
18. Рассчитайте амплитуду потенциала действия нервного волокна при следующих
концентрациях ионов: К+ i = 15510-3моль/л, К+о = 410-3моль/л, Na+i = 12 10-
3моль/л, Na+o = 145 10-3моль/л, температура Т = 310 К.

19. Определите среднюю силу, действующую на барабанную перепонку уха человека !!!! (была 3, которая неправильная)
(площадь S = 66 мм2) для двух случаев: а) порог слышимости; б) порог болевого
ощущения. Частота равна 1кГц.
Дано: S=66мм2; n=1кГц
Найти: F0-?; Fбол-?
Решение:
I=ΔP2/(2p(
ро)V) I-интенсивность; P-плотность среды; p(ро)-плотность среды; V-скорость звука
I0=10-12 Вт/м2 — Р0=20*10-5Па
Iб=10 Вт/м2 — Рб=60Па
Lр=20lg P/P0 (дБ)
P=F/S
F0=P0S=2*10-5*66*10-6=132*10-11=1,32*10-9Н=1,32мН
Fб=PбS=60*66*10-6=3960=3,96*10-3Н=3,96мН
Ответ: F0=1,32мН; Fб=3,96мН
20. Уровень громкости звука частотой V(ню) = 5000 Гц равен Е = 50 фон. Найдите
интенсивность этого звука.
Дано: V(ню)=5000Гц; Е=50 фон
Найти: I=? (Вт/м2)
Решение: V(ню) – частота, Е – уровень громкости звука, I – интенсивность звука, I0 – порог слышимости, L – уровень интенсивности
Е=10 Lg I/I0 (фон), т.к. V ≠1000 Гц, то используем изофоны
1) L=52 дБ
L=10 Lg I/I0
Lg I/I0 = L/10
I/I0 = 10 L/10
I = I0 *10 L/10
I = 10-12 * 1052/10 = 10-6.8 Вт/М2
Ответ : 10-6.8 Вт/М2
21. Шум на улице, которому соответствует уровень интенсивности звука L1 = 50 дБ,
слышен в комнате так, как шум L2 = 30 дБ. Найдите отношение интенсивности звука на
улице и в комнате.
Дано: L1= 50 дБ = 5 Б, L2= 30 дБ=3Б.
Найти: I1/I2=?
Решение: L1= lg I1/I0 ; L2= = lg I2/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
5 = lg I1/I0 3=lg I2/I0
I1 = I0 * 105 I2 = I0 *103
105/103 = 100
Ответ : 100
22. Отношение интенсивностей двух источников звука равно: I2/I1=4. Чему равна
разность уровней интенсивностей этих звуков?
Дано: I2/I1=4 .
Найти: L2-L1 -?
Решение:
L=10lg I/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
L2-L1=10lg I2/I0 – 10lg I1/I0= 10 (lg I2 –lg I0 – (lg I1 – lg I0))= 10(lg I2 – lg I1)= 10 lg I2/I1= 10 lg 4 ≈6
Ответ: 6 (дБ?)
23. В лабораторном цехе уровень интенсивности шума достигла 80 дБ. С целью
уменьшения шума было решено обить стены этого помещения материалом поглощающим
звук, который уменьшает интенсивность звука в 1000 раз. Какой уровень интенсивности
шума станет после этого в этом помещении?
Дано: L1=80дБ ;
Найти: L2-?
Решение: определим интенсивность звука
L1=10lg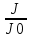
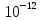
При изменении интенсивности звука изменение уровня интенсивности будет равно:
Ответ: 50дБ
24. Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль
упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки
сосуда равное 6, а плотность сосудистой стенки равна 1,15 г/см3.
Дано: V=8м/с; р
(ро)=1,15г/см Найти: I1/I2=?
Решение: L1= lg I1/I0 ; L2= = lg I2/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
5 = lg I1/I0 3=lg I2/I0 I1 = I0 * 105 I2 = I0 *103
105/103 = 100
Ответ : 100
25. Какова должна быть разность давлений Р на концах капилляра радиуса r = 1 мм и
длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1
см3 воды (коэффициент вязкости η1 = 10-3 Па·с) или глицерина (η2 = 0,85 Па·с)?
Дано: r =1мм= 10¯³м, L=1см=0,1м, t=5с, V=1см³=1·10¯⁶м³, ŋ1=10¯³Па·с, ŋ2=0,85Па·с
Найти: ∆Р-?
Решение: Q=∆Р/x
t-время, ŋ-вязкость, x-гидравлич сопротивление, Q- обьем, L-длина, R-радиус
26. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость
течения крови: υ1 = 0,5 мм/с. Средняя скорость тока крови в аорте составляет υ2 = 40 см/с.
На основании этих данных определить, во сколько раз суммарная площадь сечений
функционирующих капилляров больше площади сечения аорты.
Условие неразрывности струи было получено для трубки тока переменного сечения
Дано: Vкап=0,5мм/с; Vаорт.средн=40см/c;
Найти: 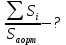
Решение:
27. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое
значение числа Рейнольдса может снизиться до 1160. Определить скорость, при которой
возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм.
Плотность крови 1050 кг/м3, вязкость крови 5. 10-3Па·с.
Дано: d=2,5мм=2,5·10¯³м, ρ=1050кг/м³, ŋ=5·10¯³Па·с, Re=1160
Найти: Vперехода-?
Решение: ρж-плотность жидкости,Vпер-скорость перехода, D-диаметр сосуда, ŋ-коэф вязкости
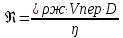

28. Во сколько раз изображение предмета на сетчатке глаза меньше самого предмета,
находящегося на расстоянии 30 м от наблюдателя? Фокусное расстояние оптической
системы глаза принять равным 1,5 см.
Дано: а=30 м; F=1,5 см


а h
Из рисунка следует ,что изображение будет перевернутым, уменьшенным и действительным.
Составим пропорцию:
Ответ: Изображение предмета на сетчатке глаза меньше самого предмета в 2000 раз
29. При максимальной аккомодации радиус кривизны передней поверхности
хрусталика изменяется от 10 до 5,5 мм, задней – соответственно от 6 до 5,5 мм. На
сколько, при этом увеличится оптическая сила хрусталика. Показатель преломления
хрусталика 1,424, в окружающей среде 1,336.
Дано: R1=10mm; R11=5,5mm; R2=6mm; R21=5,5mm; nхр=1,424; nср=1,336
Найти:
Решение: при максимально аккомодации изменяется кривизна хрусталика. Он становится более выпуклым(F уменьшается) и его оптическая сила возрастает т.е. D2>D1
Оптическая плотность линзы вычисляется по формуле: D=(n1;2-1)(±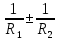
D-оптическая сила [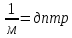
R1 и R2— радиусы кривизны ограничивающих сферических поверхностей.
n1;2 =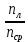
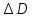
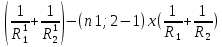
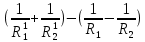
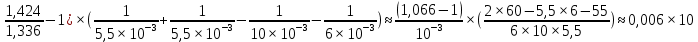
Ответ: при максимальной аккомодации оптическая сила хрусталика увеличена примерно на 6 дптр
30. Показатели преломления двух сред равны 1,5263 и 1,1275. Найти предельный угол преломления.
Дано: n1=1.5263 n2=1.1275
Найти: 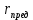
Решение:
закон преломления света Ф. Снеля
r-угол преломления, i-угол падения, n1 – показатель преломления 1 среды, n2 — показатель преломления 2 среды
Выразим: 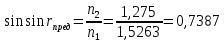
Ответ:
31. Оптическая сила линзы составляет 5 дптр. Чему равно фокусное расстояние линзы?
Дано: D=5 дптр. Найти: F -?
Решение: 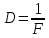
Ответ: 20cm фокусное растояние линзы
32. Оптическая сила хрусталика для человека с нормальным зрением равна 25 дптр.
Показатель преломления 1,4. Вычислите радиусы кривизны хрусталика, если известно,
что один радиус кривизны в 2 раза больше другого.
Дано: D = 25 дптр N = 1,4 R2= 2R1
Найти: R1 — ? R2 — ?
Решение: Хрусталик можно считать тонкой линзой, поэтому для него будет справедлива формула тонкой линзы 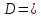
Где D – оптическая сила хрусталика F – фокусное растояние n – относительный показатель преломления хрусталика, R1 и R2 – радиусы кривизны поверхностей хрусталика.
Используя условие задачи R2=2R1, получаем
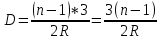
R2=2.4*2=4.8мм
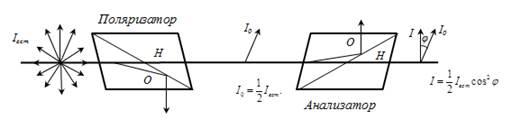
33. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через эти призмы, уменьшилась в 4 раза? Поглощением света пренебречь.
Дано:
Найти: 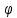
Решение:
Закон Маллюса
Iана-интенсивность поляризованного света прошедшего анализатор
Iпад-интенсивность поляризованного света падающего на анализатор
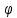
Интенсивность естественного света, прошедшего поляризатор, уменьшается в 2 раза, то есть
Ответ:45
34. Главные плоскости двух призм Николя, поставленных на пути луча, образуют между собой угол 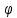
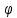
Дано: φ1=60°, φ2=30°
Найти: как изменится интенсивность света?
РЕШЕНИЕ: 1) I (прош)=I под cos²φ
2) a = I прош / I под = cosφ1
b = I прош / I под = cosφ2
3) b/a= cos²φ2 / cos²φ1 = cos²20/ cos²60 = (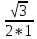
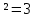
ОТВЕТ: Интенсивность света, прошедшего через призмы, если угол между их плоскостями поляризации станет равным φ2=30° увеличившись в 3 раза.
35. Коэффициент пропускания раствора τ=0,3. Чему равна его оптическая плотность? Если известна оптическая плотность раствора D=0,08, чему равен коэффициент пропускания?
Дано: T=0.3 D=0.08 Найти: D=?
Решение: 1) D=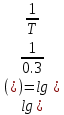
2) 0,08=lg(
T-коэффициент пропускания
D-оптическая плотность
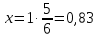
36. Чему равен молярный показатель поглощения вещества, если при прохождении света через раствор с концентрацией 0,5 моль интенсивность света уменьшилась в 10 раз? Длина кюветы 0,3 см.
Дано: С=0,5 моль l=0,3 см Найти: Е-?
Решение: 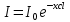
Оптическая плотность раствора или вещества это отношение падающего и преходящего света
lg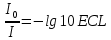
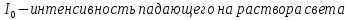
С – Концентрация окрашенного вещества, моль/л
l-длина кюветы
lg10=E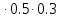
1=E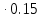
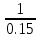
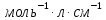
Ответ: Молярный показатель поглощения вещества Е=6.7 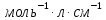
37. Найдите границу тормозного рентгеновского излучения (частоту и длину волны) для напряжений и1=2 кВ и и2=20 кВ. Во сколько раз энергия фотонов этих излучений больше энергии фотона, с длиной волны λ =760 нм.
Эксперимент показывает, что приложенное к регненовской трубке напряжение U, связано с длинной волны λ
λ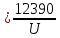
Частоты для этих длин волн:
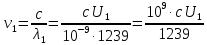
C – скорость света.
Теперь сравним энергии фотонов с длинами волн
Энергия фотона 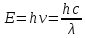
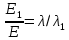
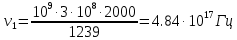
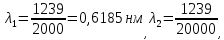
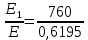
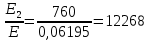
Ответ: длины волн 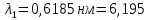
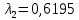
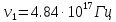
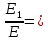
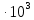
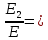
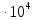
38. Найдите поток рентгеновского излучения при разности потенциалов на
рентгеновской трубке 15 кВ и силе тока 3 мА. Анод изготовлен из вольфрама. Скольким
фотонам в секунду соответствует этот поток, если допустить, что излучается
электромагнитная волна, длина которой равна 1/2 от длины волны, соответствующей
границе спектра тормозного рентгеновского излучения.
Поток Ф излучения от ренгеновской трубки починяется соотношению:
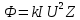
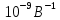
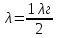
N=Ф/hν , где h – постоянная планка. Связь частоты с длиной волны имеет вид
ν=с/λ , где с – скорость света
N = Фλ/hc =>
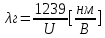
Ответ: поток 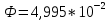
39. Мощность экспозиционной дозы γ-излучения на расстоянии R = 1 м от точечного источника составляет р=2,15*10-7 Кл/кг. Определите минимальное расстояние от источника, на котором можно ежедневно работать по 6 ч без защиты. Предельно допустимой эквивалентной доз при профессиональном облучении считать 5*10-2 Дж/кг в течение года. Поглощение γ -излучения воздухом не учитывать.
I – интенсивность электромагнитных волн
А – активность элемента Е – энергия порции излучения R – радиус сферы
Далее можно посчитать величину заряда в слое толщиной 1 см
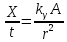
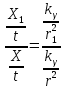
Следовательно, мощность экспозиционной дозы
Тогда
Величина 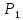
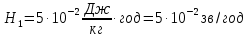
Тут К=1, так как в условии задачи сказано об источнике 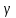
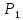
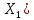
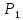
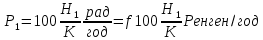
Возьмем р=2,15*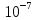
Ответ: нужно удалиться от источника 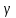
40. Какова активность препарата, если в течение 10 мин распадается 10 000 ядер этого вещества?
По определению активностью препарата называется число распавшихся ядер за единицу времени (секунду, минуту, час). Если препарат имеет период полураспада больше суток, то можно считать, что количество распадов за единицу времени остается постоянным, при недолгом наблюдении за препаратом. Тогда искомая активность А будет равна
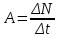
Ответ: активность препарата А = 16,7 Бк.
41. Работа выхода электрона из лития А = 2,5 эВ. Будет ли фотоэффект при освещении
лития монохроматическим светом с длиной волны 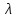
Дано: 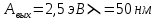
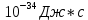
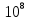
Найти: Будет ли фотоэффект?
Решение: 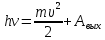
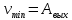
Ответ: λ<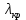
Подборка по базе: Судебное решение для курсовой.docx, ПР№1 Решение.docx, 1 Планируемые изменения инфраструктуры.docx, Дело 12-0272_2021. Решение по жалобе_протесту на постановление (, Квадратные уравнения. Решение неполных кв.ур..ppt, !!! готовое решение задач с формулами.doc, Бухгалтерский баланс ЗАО Стэк и решение.docx, Готовое решение_ Как произвести увольнение работника по медицинс, ОБОБЩЕНИЕ ПО ТЕМЕ Изменения с вещвами.docx, раздаточный материал к уроку решение задач на дроби.docx
1.Термодинамической системе было передано тепло в количестве 140 Дж, а также над ней была совершена работа в 65 Дж. Как изменилась внутренняя энергия системы в этом процессе?
Дано: Q=140 Дж. A=65 Дж. Найти: dU=?
Решение: Запишем формулу изменения внутренней энергии:
Где A — работа совершенная над газом (Работа внешних сил), Q — кол-во теплоты, переданное данной системе. Осталось посчитать:
dU=140+65=205 Дж=0.205кДж.
Ответ: dU=0.205кДж
2. Определите калорический коэффициент кислорода при окислении глюкозы, если из экспериментов с калориметрической бомбой известно, что при окислении 1 г глюкозы выделяется 15,7 кДж теплоты.
Задача 3. Сколько полезной работы может быть получено при сжигании 12*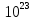
Дано: V = 12*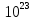
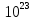
Найти- А (полезную)
Решение: Теплота сгорание глюкозы Q=2800 кДж/моль. согласно справочнику
КПД (n) = A Q *100%
Na=Число Авогадро 6,022*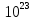
Q- Количество теплоты полученное рабочим телом от нагревателя
А — полезная работа, совершаемая рабочим телом за цикл
Тогда A=nQV=0,5*2800*2=2800 кДж.
Ответ: 2800 кДж.
4. Спортсмен, пробегая дистанцию, выделяет за 1 мин 90 л воздуха, в котором содержится
12% кислорода и 8% углекислого газа. Каков расход энергии спортсмена за 5 мин
дистанции?
Дано: t1=1час, V=90л, VO2=12%, VCO2=8%, t2=5 мин
Найти: E-?
Решение: В 100мл 21% O2 и 0,003 CO2
Расход O2 на 100мл VO2= 21-12=9%=9мл O2
Расход CO2 на 100мл VCO2=8%=8мл CO2
ДК-дыхательный коэффициент ДК= VCO2/ VO2=8/9=0,88
КК-калорический коэффициент ДК=0,88=КК=20,515 кДЖ
В 100мл – 9 мл В 90000мл- Хмл
Х=90000 х 9/100= 8100мл
За 1 минуту 1000 мл – 20,515кДЖ
8100мл- Х
Х= 20,515 х 8100/1000=166кДЖ
За 5 минут Е=166кДЖ х 5= 830кДЖ
Ответ: Е= 830 кДЖ
5. Удельная электрическая емкость мембраны аксона, измеренная внутриклеточным микроэлектродом, оказалась равной 0,5 мкФ/см^2. По формуле плоского конденсатора оценить толщину гидрофобного слоя мембраны с диэлектрической проницаемостью равной 2.
Дано: C=0,5 мкФ/см^2 E=2
Найти: h-?
Решение: C=Eo*E*S/h-выражение для емкости плоского конденсатора, где С-емкость
Е-относительная диэлектрическая проницаемость
Ео=8,85*10^-12 Ф/м-диэлектрическая постоянная
S-площадь обкладки конденсатора (мембраны аксона)
h-толщина гидрофобного слоя мембраны
Cуд.=C/S=0,5*10^-6/(10^-2 м)^2=0,5*10^-2 Ф/м^2
Е=Ео/Е>1
выражаем h:
h=EoES/C=EoE/Cуд.= 2*8,85*10^-12/0,5*10^-2=35,4*10^-10=3,5 Нм
Ответ: 3,5 Нм
6. Используя уравнение Эйнштейна Sкв = 2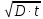
диффузии, определите, какое расстояние на поверхности мембраны эритроцита проходит
молекула фосфолипида за 1 секунду в результате латеральной диффузии? D принять равным 10-
12 м^2с.Сравните с окружностью эритроцита диаметром 8 мкм.
Дано: 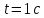
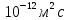
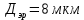
Решение:
Sкв = 2
Sкв=2 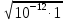
l) (длина окружности)=2ПR=2Пd (п-число пи, d-диаметр
1секунда=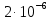
x =3.14*8
решаем пропорцию
x=(3,14*8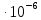
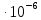
x=12,28 с Ответ: 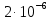
7. Микровязкость мембраны эритроцита при температуре 37С равна 6 Пз. Найти величину коэффициента диффузии для ионов кальция. Если радиус негидратированного иона кальция 1,5 нм.
Дано: Т=37С, n=6 Пз, r=1,5 нм, k(постоянная Больцмана)=1, 38х10^-23Дж/К, число пи=3,14
Найти: D=? – величину коэффициента диффузии
Решение:
1.) Т=37С=310К, n(микровязкость)=6 Пз, k(постоянная Больцмана)=1, 38х10^-23Дж/К, r(радиус)=1,5нм, пи(число)=3,14.
3.) Найдем искомое по формуле: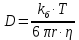
Ответ: D=
8. Бислойная липидная мембрана (БЛМ) толщиной 10 нм разделяет камеру на две части. Плотность потока метиленового синего через БЛМ постоянна и равна 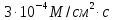
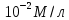
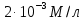
Дано: h = 10 нм = 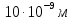
С0 = 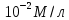
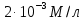
Найти: D-?
Решение:
Воспользуемся уравнением Фика:
J = — D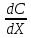
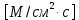
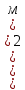
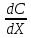
D=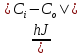
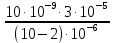
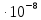
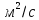
Ответ: 3.75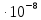
9. Концентрация глюкозы в клетке равна 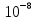
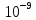
Дано:
[Гл]i=10-8 моль/л [Гл]o=10-9 моль/л T=20о C=293К N=10 моль
Найти: Δµ (в клетку) Δµ (из клетки)
Решение: µ=µ0+RT*lnC
µ-химический потенциал, Дж/моль µо-стандартный химический потенциал, Дж/моль
R=8,3 – газовая константа, (Дж/(моль*К) T(к)-температура С [число молей]-концентрация
В клетку: Δµ=µо-µi=µ0o+RT*lnCo-µ0i + RT*lnCi=RT*ln(Co/Ci)=8,3*293*ln(10-9/10-8)=-2432*2,3lg10=-5594 [Дж/моль]
-5,6 [кДж/моль] < 0 (Пассивная диффузия)
Из клетки: Δµ=µi— µо= µ0i+RT*lnCi — µ0o+RT*lnCo=8,3*293*ln(10-9/10-8)=2432*2,3lg10=5594 Дж/моль5,6 кДж/моль>0 (Только активный транспорт)
10. Найти приращение электрохимического потенциала при транспорте кальция из клетки и в клетку, если концентрация кальция в клетке равна 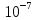
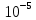
Дано: Ci(Ca)=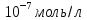
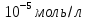
T=20C=293K L(фи)=(-60)мВ
Найти:
u1-? u2-?
Решение: u=R•T•ln•(-Co/Ci) +ZF(Lo+L1)
u- химический потенциал
R=8,3 [Дж/моль•К] газовая постоянная
F= постоянная Фарадея
Z= 2 валентность ионов
Со=внеклеточная концентрация иона
Сi= внутриклеточная концентрация иона
M=Mo+R•T•ln 10-5/10-7 + 2•9,6 •60= 8,3•293• ln 10^2 +2•9,6•60=11186,74+1152=
12338,7 Дж/моль=12,3 КДж/моль.
11. Концентрация ионов натрия в клетке 1 ммоль/л, вне клетки 180 ммоль/л. Разность потенциалов на мембране (- 80 мВ). Можно ли осуществить активный транспорт ионов натрия при помощи натрий-калиевого насоса из клетки на наружную поверхность мембраны, при температуре 37 С, изменение свободной энергии при гидролизе 1 моль АТФ = (- 45) кДж/моль, КПД насоса 50%.
Дано: {Na}i= 1мМ {Na}o=180 мМ t=37
Разность потенциалов 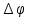
12. Концентрация глюкозы в плазме крови 3,5 мМ/л, концентрация глюкозы в
эритроците 5 мМ/л. Концентрация ионов Na+ в эритроците 4 мМ/л, а в плазме 140
мМ/л, температура 37С. Можно ли транспортировать молекулу глюкозы в
эритроцит, используя вторичный активный транспорт. Разность потенциалов на
мембране эритроцита (-60) мВ.
13. Какое количество одновалентных ионов нужно переместить на наружную поверхность мембраны из клетки, чтобы сохдать потенциал покоя 120мВ? Площадь поверхности мембраны 10-9 м2, удельная электроёмкость мембраны Суд=10-2 Ф/м2.
Дано: 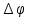
Решение:
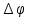
1. С=Суд*S=10-2*10-9=10-11Ф — электроёмкость мембраны.
2. Заряд поверхности мембраны находим через ёмкость: q=C*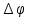
3. Число ионов, образующих такой заряд, рано n=q/e=10-12/1,6*10-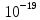
Ответ: n=6,2*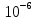
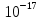
14. Найдите, какой должна быть концентрация ионов калия в клетке, при которой
величина равновесного калиевого потенциала равна (-100) мВ, при температуре 37оС,
[K+]o = 6х10-3 моль/л
Дано:
Найти: Сi — ?
Решение:
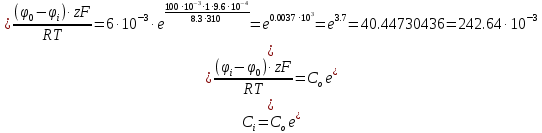
15. Определите равновесный мембранный потенциал при отношении концентраций
натрия снаружи и внутри а) 1:1; б) 10:1; в) 100:1, температура Т = 310 К
Дано:
[Na+]o/[Na+]i=1/1
[Na+]o/[Na+]i=10/1
[Na+]o/[Na+]i=100/1
T=37°C
Найти:
Дельта фи
Решение:
(Фи) yi-yo=RT/ZF•ln[Na+]o/[Na+]i
R- 8,3 [дж/моль•К°] газовая константа
T[К°]- температура
Z[1]- валентность иона
F- 9,6•10^4 [кл/моль]
yi-yo- равновесный потенциал [B]
RT/ZF=8,3•310/1•9,6•10^4=268•10^4=268•10^1•10^-3=27[мВ]
а)yi-yo=27ln1/1=0 [мВ]
б)yi-yo=27ln10/1=27•2,3lg10=62 [мВ]
в)yi-yo=27ln100/1=27•2,3lg10^2=124 [мВ]
16. Чему равна напряженность электрического поля на мембране в состоянии покоя,
если концентрация ионов калия внутри клетки 125 ммоль/л, снаружи – 2,5 ммоль/л, а
толщина мембраны 8 нм?
Дано:[К+]i=125 ммоль/л [К+]о=2,5 ммоль/л
h=8 нм=8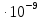
Найти: Е-?
Решение:
Е= — (Фi-Фо)/h
Фi-Фо=RT/ZF * ln(Co/Ci)
Фi-Фо= ((8,31*310)/(1*96485)) * ln ((2.5*10^-3)/(125*10^-3))=-0,105 Вольт
Е= (0,105/8*10^-9)= 0,013 *10^-9 В/м
*Пояснения*
Е — напряжённость эл.поля
Фi-Фо разность потенциалов
h — толщина мембраны
R- газовая постоянная(8,31дж/моль*К)
Т — температура (310 К)
С- концентрация
17. Определите равновесный мембранный потенциал митохондрий, если при 37 ͦС внутри митохондрий pH=9, а в окружающей среде рН=7.
Дано: T=37°C = 310 K
pH(i) = 9 pH(o)= 7
Найти:
∆(фи)=?
Решение:
Равновесный мембранный потенциал можно рассчитать с помощью формулы Нернста:
1) ∆(фи) = (фи i) — (фи o) = RT/ZF * Ln C(o)/C(i),
где (фи i) — потенциал на внутренней части мембраны, (фи o) — потенциал на внешней части мембраны, R — газовая постоянная, Т-температура, Z- валентность ионов, F — постоянная Фарадея, Со-концентрация ионов снаружи клетки, Сi- концентрация ионов внутри клетки.
Водородный показатель рН определяется как
2) рН=-lg[H^+],
где величина [Н^+] имеет размерность моль/л и по своей сути является концентрацией. Вычислим концентрацию протонов (ядер атомов водорода) по величине рН:
3) C=[H^+]=10^-pH.
Тогда объединение (1) — (3) позволяет записать:
4) ∆(фи) =RT/ZF * ln * 10^-pHo / 10^-pHi ==RT/ZF * ln * 10^pHo / 10^pHi =RT/ZF * ln * 10^(pHi — pHo) = RT/ZF*(pHi — pHo) * ln10
Подставим числа в выражение (4) :
∆(фи) =(8.31 Дж/моль*К * 310 К / 1*96500Кл/моль ) *(9-7) ln10=0,123 Дж/К =123мВ
Ответ: ∆(фи) = 123 мВ
18. Рассчитайте амплитуду потенциала действия нервного волокна при следующих
концентрациях ионов: К+ i = 15510-3моль/л, К+о = 410-3моль/л, Na+i = 12 10-
3моль/л, Na+o = 145 10-3моль/л, температура Т = 310 К.

19. Определите среднюю силу, действующую на барабанную перепонку уха человека !!!! (была 3, которая неправильная)
(площадь S = 66 мм2) для двух случаев: а) порог слышимости; б) порог болевого
ощущения. Частота равна 1кГц.
Дано: S=66мм2; n=1кГц
Найти: F0-?; Fбол-?
Решение:
I=ΔP2/(2p(
ро)V) I-интенсивность; P-плотность среды; p(ро)-плотность среды; V-скорость звука
I0=10-12 Вт/м2 — Р0=20*10-5Па
Iб=10 Вт/м2 — Рб=60Па
Lр=20lg P/P0 (дБ)
P=F/S
F0=P0S=2*10-5*66*10-6=132*10-11=1,32*10-9Н=1,32мН
Fб=PбS=60*66*10-6=3960=3,96*10-3Н=3,96мН
Ответ: F0=1,32мН; Fб=3,96мН
20. Уровень громкости звука частотой V(ню) = 5000 Гц равен Е = 50 фон. Найдите
интенсивность этого звука.
Дано: V(ню)=5000Гц; Е=50 фон
Найти: I=? (Вт/м2)
Решение: V(ню) – частота, Е – уровень громкости звука, I – интенсивность звука, I0 – порог слышимости, L – уровень интенсивности
Е=10 Lg I/I0 (фон), т.к. V ≠1000 Гц, то используем изофоны
1) L=52 дБ
L=10 Lg I/I0
Lg I/I0 = L/10
I/I0 = 10 L/10
I = I0 *10 L/10
I = 10-12 * 1052/10 = 10-6.8 Вт/М2
Ответ : 10-6.8 Вт/М2
21. Шум на улице, которому соответствует уровень интенсивности звука L1 = 50 дБ,
слышен в комнате так, как шум L2 = 30 дБ. Найдите отношение интенсивности звука на
улице и в комнате.
Дано: L1= 50 дБ = 5 Б, L2= 30 дБ=3Б.
Найти: I1/I2=?
Решение: L1= lg I1/I0 ; L2= = lg I2/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
5 = lg I1/I0 3=lg I2/I0
I1 = I0 * 105 I2 = I0 *103
105/103 = 100
Ответ : 100
22. Отношение интенсивностей двух источников звука равно: I2/I1=4. Чему равна
разность уровней интенсивностей этих звуков?
Дано: I2/I1=4 .
Найти: L2-L1 -?
Решение:
L=10lg I/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
L2-L1=10lg I2/I0 – 10lg I1/I0= 10 (lg I2 –lg I0 – (lg I1 – lg I0))= 10(lg I2 – lg I1)= 10 lg I2/I1= 10 lg 4 ≈6
Ответ: 6 (дБ?)
23. В лабораторном цехе уровень интенсивности шума достигла 80 дБ. С целью
уменьшения шума было решено обить стены этого помещения материалом поглощающим
звук, который уменьшает интенсивность звука в 1000 раз. Какой уровень интенсивности
шума станет после этого в этом помещении?
Дано: L1=80дБ ;
Найти: L2-?
Решение: определим интенсивность звука
L1=10lg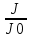
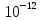
При изменении интенсивности звука изменение уровня интенсивности будет равно:
Ответ: 50дБ
24. Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль
упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки
сосуда равное 6, а плотность сосудистой стенки равна 1,15 г/см3.
Дано: V=8м/с; р
(ро)=1,15г/см Найти: I1/I2=?
Решение: L1= lg I1/I0 ; L2= = lg I2/I0
L-уровень интенсивности (дБ), I – интенсивность (Вт/м2), I0 – порог слышимости = 10-12 Вт/м2
5 = lg I1/I0 3=lg I2/I0 I1 = I0 * 105 I2 = I0 *103
105/103 = 100
Ответ : 100
25. Какова должна быть разность давлений Р на концах капилляра радиуса r = 1 мм и
длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1
см3 воды (коэффициент вязкости η1 = 10-3 Па·с) или глицерина (η2 = 0,85 Па·с)?
Дано: r =1мм= 10¯³м, L=1см=0,1м, t=5с, V=1см³=1·10¯⁶м³, ŋ1=10¯³Па·с, ŋ2=0,85Па·с
Найти: ∆Р-?
Решение: Q=∆Р/x
t-время, ŋ-вязкость, x-гидравлич сопротивление, Q- обьем, L-длина, R-радиус
26. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость
течения крови: υ1 = 0,5 мм/с. Средняя скорость тока крови в аорте составляет υ2 = 40 см/с.
На основании этих данных определить, во сколько раз суммарная площадь сечений
функционирующих капилляров больше площади сечения аорты.
Условие неразрывности струи было получено для трубки тока переменного сечения
Дано: Vкап=0,5мм/с; Vаорт.средн=40см/c;
Найти: 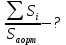
Решение:
27. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое
значение числа Рейнольдса может снизиться до 1160. Определить скорость, при которой
возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм.
Плотность крови 1050 кг/м3, вязкость крови 5. 10-3Па·с.
Дано: d=2,5мм=2,5·10¯³м, ρ=1050кг/м³, ŋ=5·10¯³Па·с, Re=1160
Найти: Vперехода-?
Решение: ρж-плотность жидкости,Vпер-скорость перехода, D-диаметр сосуда, ŋ-коэф вязкости
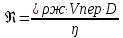

28. Во сколько раз изображение предмета на сетчатке глаза меньше самого предмета,
находящегося на расстоянии 30 м от наблюдателя? Фокусное расстояние оптической
системы глаза принять равным 1,5 см.
Дано: а=30 м; F=1,5 см


а h
Из рисунка следует ,что изображение будет перевернутым, уменьшенным и действительным.
Составим пропорцию:
Ответ: Изображение предмета на сетчатке глаза меньше самого предмета в 2000 раз
29. При максимальной аккомодации радиус кривизны передней поверхности
хрусталика изменяется от 10 до 5,5 мм, задней – соответственно от 6 до 5,5 мм. На
сколько, при этом увеличится оптическая сила хрусталика. Показатель преломления
хрусталика 1,424, в окружающей среде 1,336.
Дано: R1=10mm; R11=5,5mm; R2=6mm; R21=5,5mm; nхр=1,424; nср=1,336
Найти:
Решение: при максимально аккомодации изменяется кривизна хрусталика. Он становится более выпуклым(F уменьшается) и его оптическая сила возрастает т.е. D2>D1
Оптическая плотность линзы вычисляется по формуле: D=(n1;2-1)(±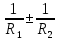
D-оптическая сила [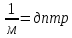
R1 и R2— радиусы кривизны ограничивающих сферических поверхностей.
n1;2 =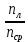
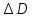
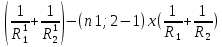
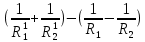
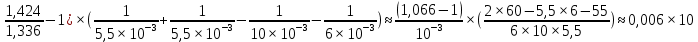
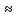
Ответ: при максимальной аккомодации оптическая сила хрусталика увеличена примерно на 6 дптр
30. Показатели преломления двух сред равны 1,5263 и 1,1275. Найти предельный угол преломления.
Дано: n1=1.5263 n2=1.1275
Найти: 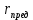
Решение:
закон преломления света Ф. Снеля
r-угол преломления, i-угол падения, n1 – показатель преломления 1 среды, n2 — показатель преломления 2 среды
Выразим: 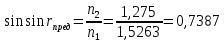
Ответ:
31. Оптическая сила линзы составляет 5 дптр. Чему равно фокусное расстояние линзы?
Дано: D=5 дптр. Найти: F -?
Решение: 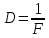
Ответ: 20cm фокусное растояние линзы
32. Оптическая сила хрусталика для человека с нормальным зрением равна 25 дптр.
Показатель преломления 1,4. Вычислите радиусы кривизны хрусталика, если известно,
что один радиус кривизны в 2 раза больше другого.
Дано: D = 25 дптр N = 1,4 R2= 2R1
Найти: R1 — ? R2 — ?
Решение: Хрусталик можно считать тонкой линзой, поэтому для него будет справедлива формула тонкой линзы 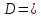
Где D – оптическая сила хрусталика F – фокусное растояние n – относительный показатель преломления хрусталика, R1 и R2 – радиусы кривизны поверхностей хрусталика.
Используя условие задачи R2=2R1, получаем
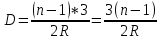
R2=2.4*2=4.8мм
33. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через эти призмы, уменьшилась в 4 раза? Поглощением света пренебречь.
Дано:
Найти: 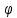
Решение:
Закон Маллюса
Iана-интенсивность поляризованного света прошедшего анализатор
Iпад-интенсивность поляризованного света падающего на анализатор
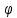
Интенсивность естественного света, прошедшего поляризатор, уменьшается в 2 раза, то есть
Ответ:45
34. Главные плоскости двух призм Николя, поставленных на пути луча, образуют между собой угол 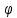
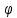
Дано: φ1=60°, φ2=30°
Найти: как изменится интенсивность света?
РЕШЕНИЕ: 1) I (прош)=I под cos²φ
2) a = I прош / I под = cosφ1
b = I прош / I под = cosφ2
3) b/a= cos²φ2 / cos²φ1 = cos²20/ cos²60 = (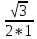
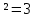
ОТВЕТ: Интенсивность света, прошедшего через призмы, если угол между их плоскостями поляризации станет равным φ2=30° увеличившись в 3 раза.
35. Коэффициент пропускания раствора τ=0,3. Чему равна его оптическая плотность? Если известна оптическая плотность раствора D=0,08, чему равен коэффициент пропускания?
Дано: T=0.3 D=0.08 Найти: D=?
Решение: 1) D=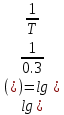
2) 0,08=lg(
T-коэффициент пропускания
D-оптическая плотность
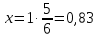
36. Чему равен молярный показатель поглощения вещества, если при прохождении света через раствор с концентрацией 0,5 моль интенсивность света уменьшилась в 10 раз? Длина кюветы 0,3 см.
Дано: С=0,5 моль l=0,3 см Найти: Е-?
Решение: 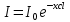
Оптическая плотность раствора или вещества это отношение падающего и преходящего света
lg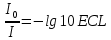
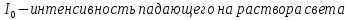
С – Концентрация окрашенного вещества, моль/л
l-длина кюветы
lg10=E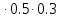
1=E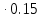
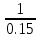
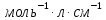
Ответ: Молярный показатель поглощения вещества Е=6.7 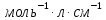
37. Найдите границу тормозного рентгеновского излучения (частоту и длину волны) для напряжений и1=2 кВ и и2=20 кВ. Во сколько раз энергия фотонов этих излучений больше энергии фотона, с длиной волны λ =760 нм.
Эксперимент показывает, что приложенное к регненовской трубке напряжение U, связано с длинной волны λ
λ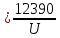
Частоты для этих длин волн:
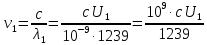
C – скорость света.
Теперь сравним энергии фотонов с длинами волн
Энергия фотона 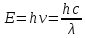
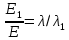
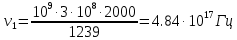
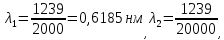
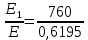
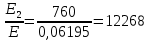
Ответ: длины волн 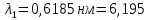
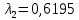
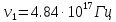
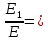
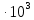
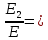
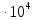
38. Найдите поток рентгеновского излучения при разности потенциалов на
рентгеновской трубке 15 кВ и силе тока 3 мА. Анод изготовлен из вольфрама. Скольким
фотонам в секунду соответствует этот поток, если допустить, что излучается
электромагнитная волна, длина которой равна 1/2 от длины волны, соответствующей
границе спектра тормозного рентгеновского излучения.
Поток Ф излучения от ренгеновской трубки починяется соотношению:
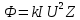
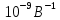
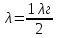
N=Ф/hν , где h – постоянная планка. Связь частоты с длиной волны имеет вид
ν=с/λ , где с – скорость света
N = Фλ/hc =>
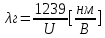
Ответ: поток 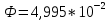
39. Мощность экспозиционной дозы γ-излучения на расстоянии R = 1 м от точечного источника составляет р=2,15*10-7 Кл/кг. Определите минимальное расстояние от источника, на котором можно ежедневно работать по 6 ч без защиты. Предельно допустимой эквивалентной доз при профессиональном облучении считать 5*10-2 Дж/кг в течение года. Поглощение γ -излучения воздухом не учитывать.
I – интенсивность электромагнитных волн
А – активность элемента Е – энергия порции излучения R – радиус сферы
Далее можно посчитать величину заряда в слое толщиной 1 см
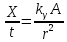
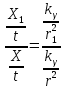
Следовательно, мощность экспозиционной дозы
Тогда
Величина 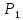
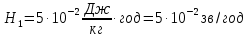
Тут К=1, так как в условии задачи сказано об источнике 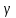
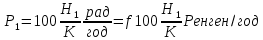
Возьмем р=2,15*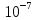
Ответ: нужно удалиться от источника 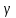
40. Какова активность препарата, если в течение 10 мин распадается 10 000 ядер этого вещества?
По определению активностью препарата называется число распавшихся ядер за единицу времени (секунду, минуту, час). Если препарат имеет период полураспада больше суток, то можно считать, что количество распадов за единицу времени остается постоянным, при недолгом наблюдении за препаратом. Тогда искомая активность А будет равна
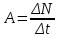
Ответ: активность препарата А = 16,7 Бк.
41. Работа выхода электрона из лития А = 2,5 эВ. Будет ли фотоэффект при освещении
лития монохроматическим светом с длиной волны 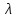
Дано: 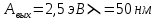
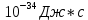
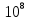
Найти: Будет ли фотоэффект?
Решение: 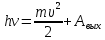
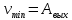
Ответ: λ<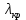
Химический состав живых клеток отличается от внешней среды, причем различия есть не только в сложных молекулах, таких как белки и нуклеиновые кислоты, но и в ионах. Например, во внеклеточной среде преобладают ионы натрия, а в клетке — ионы калия, причем последних на порядок больше. Сама по себе плазматическая мембрана клеток практически непроницаема для ионов, и поэтому для их переноса через мембрану существуют специальные транспортные механизмы — встроенные в мембрану белки. В геноме человека более 800 генов ионных каналов и транспортеров, а общую долю генов, вовлеченных в трансмембранный транспорт, оценивают в 10 % от всех генов, кодирующих белки[1]. В этой серии статей мы рассмотрим механизмы трансмембранного переноса ионов и разнообразие реализуемых ими клеточных функций. Мы также уделим внимание патологиям, вызванным мутациями в генах, кодирующих соответствующие каналы и транспортеры.
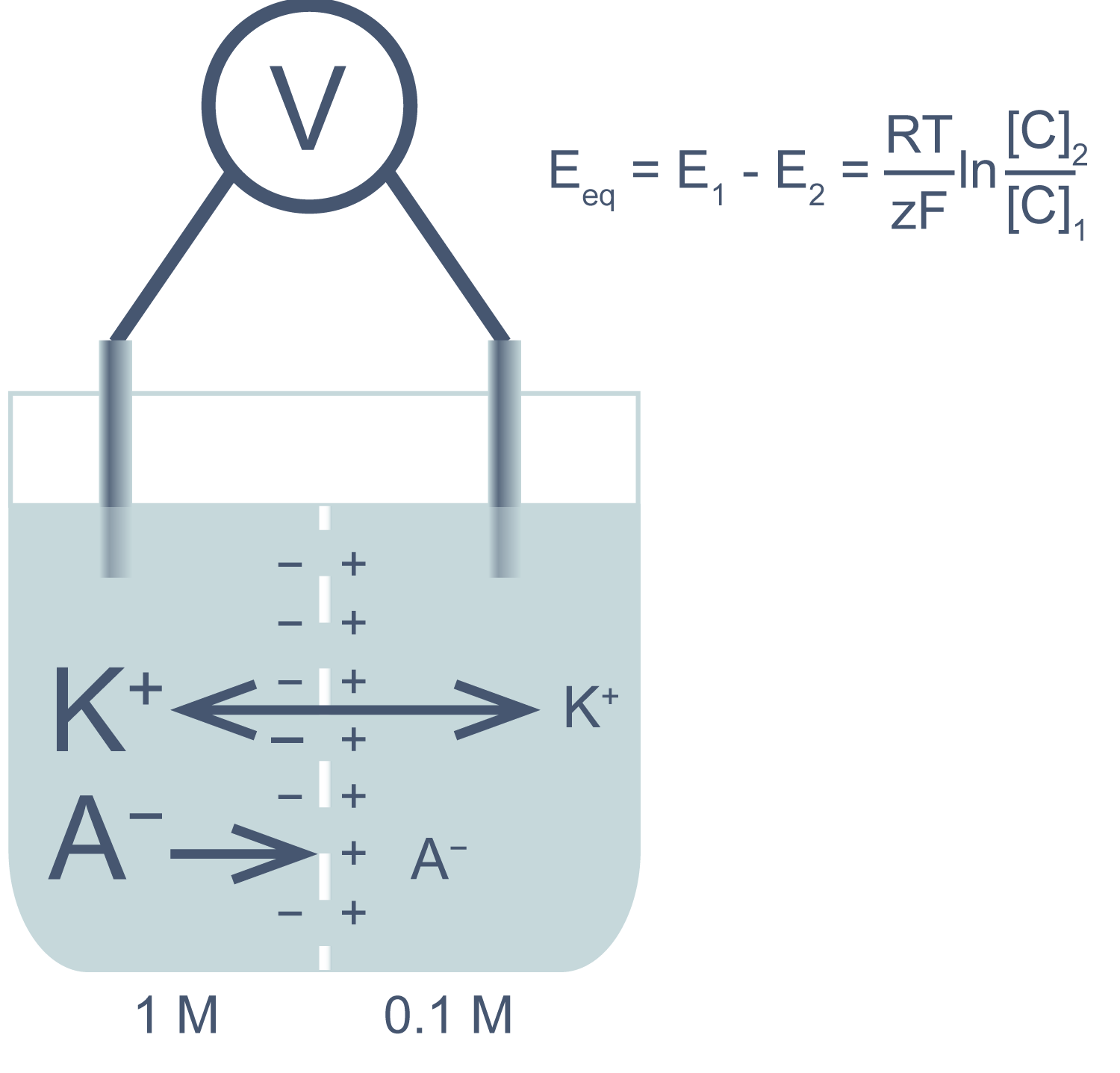
Представим себе электрохимическую ячейку — сосуд, разделенный пополам полупроницаемой мембраной, в левой части которого находится 1,0 М раствор KCl, а в правой — 0,1 М KCl. Через мембрану могут проходить катионы K+, но не анионы Cl−. Ионы K+ в результате процесса диффузии будут переходить из левого отсека в правый по градиенту концентрации*, тогда как ионы Cl−, неспособные последовать за катионами, останутся в исходном отсеке. Благодаря такому разделению зарядов на мембране будет накапливаться электрохимический потенциал: избыток анионов с левой стороны мембраны и избыток катионов с правой. Этот потенциал можно измерить, опустив в отсеки электроды, подсоединенные к вольтметру.
Асимметричный поток катионов не будет продолжаться бесконечно: накопленный электрический потенциал (с избытком положительного заряда с левой стороны мембраны) будет противодействовать диффузии ионов калия в левый отсек. Через некоторое время поток ионов K+ из правого отсека в левый сравняется по скорости с потоком из левого отсека в правый, и система достигнет равновесия. Для математического описания подобного равновесия применяют уравнение Нернста (рис. 1).
Рисунок 1 | Электрохимическая ячейка. V — вольтметр. Справа приведено уравнение Нернста, где Eeq — равновесный потенциал; E1 – E2 — разность потенциалов по обе стороны мембраны; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура (в кельвинах); F = 96485,55 Кл·моль–1 — константа Фарадея; z — степень окисления иона (его заряд); [C]1, 2 — равновесные концентрации ионов по обе стороны мембраны.
Если принять, что равновесные концентрации ионов K+ в нашем примере равны начальным, разность потенциала на мембране при 25 °C приблизительно равна –58 мВ.
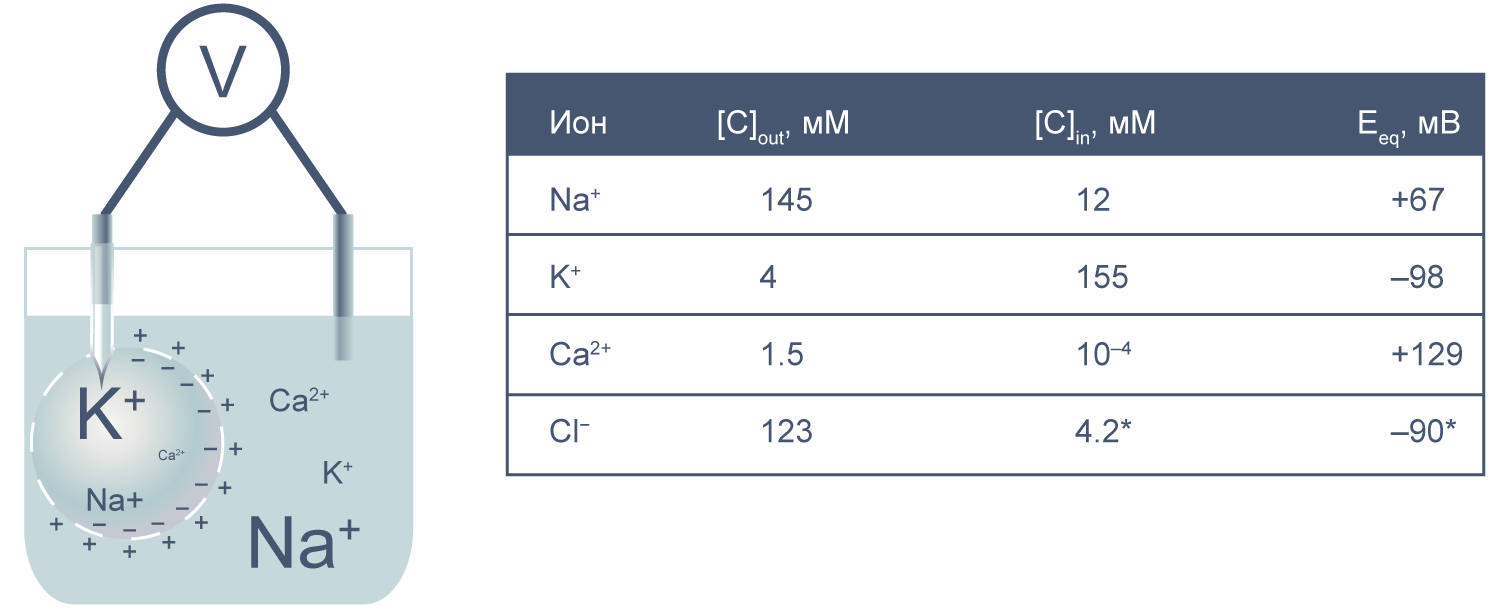
Рисунок 2 | Клетка как электрохимическая ячейка. Справа приведены концентрации основных ионов внутри и вне клетки[2].
Теперь представим, что левая часть нашей электрохимической ячейки — это живая клетка, а правая — внешняя среда. Добавим к этой картине концентрации других физиологически значимых ионов. На мембране клетки также будет накапливаться электрохимический потенциал. Величину электрической составляющей мембранного потенциала измеряют относительно потенциала вне клетки, принимая его за ноль.
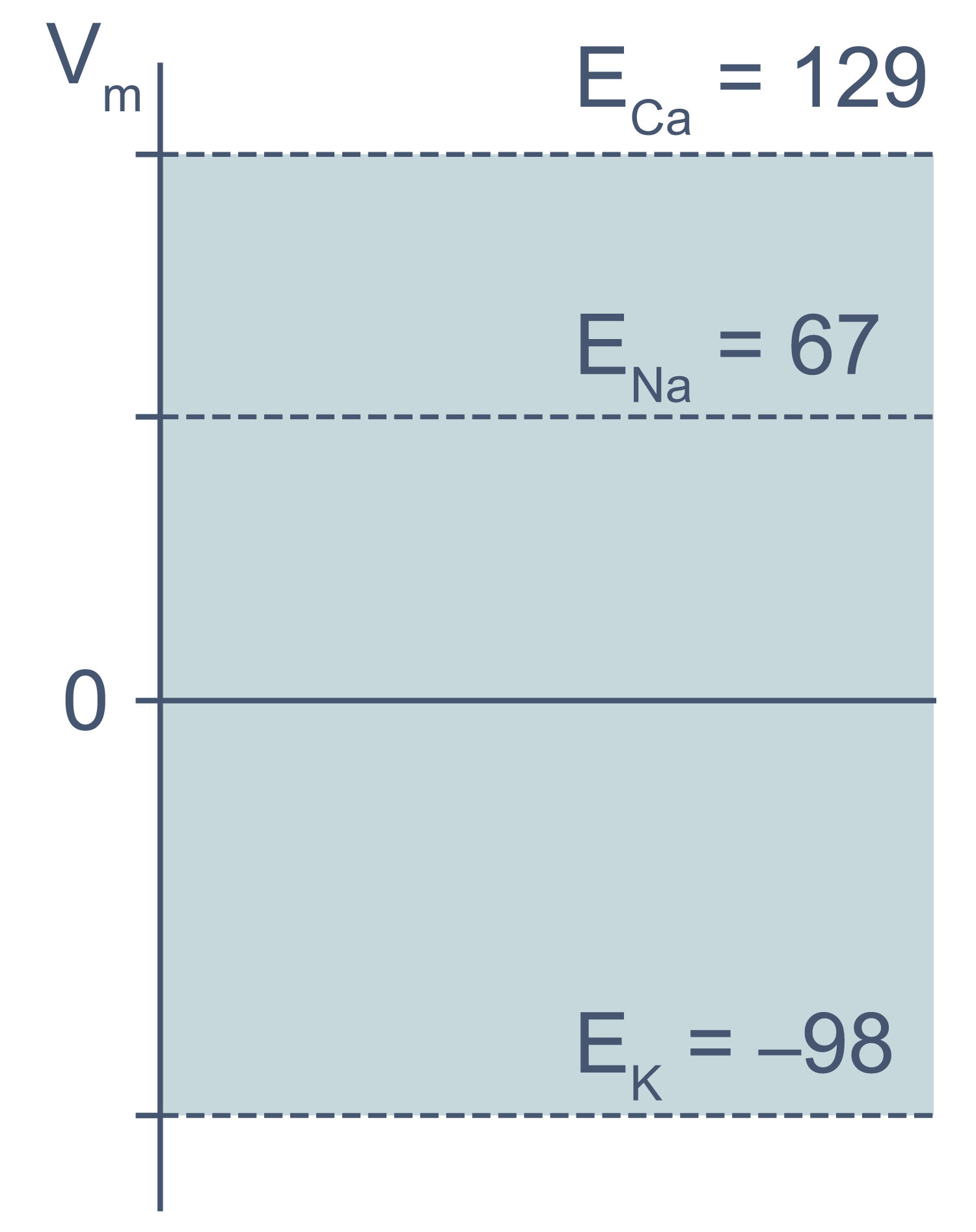
В первом приближении можно сказать, что мембрана клетки проницаема для калия и непроницаема для других катионов (Na+, Ca2+) и анионов (в первую очередь для Cl– и отрицательно заряженных участков макромолекул). Ионы калия, выходя из клетки, создают потенциал покоя. Его величина достаточно близка к значению равновесного потенциала для K+, однако строго не равна ему, поскольку в реальности другие катионы и Cl– могут участвовать в формировании потенциала покоя в различных типах клеток. Вычислив равновесные потенциалы для основных ионов, мы получим динамический диапазон величины потенциала на мембране клетки: он не может быть более отрицательным, чем EK, и не может достигать более положительных значений на пике потенциала действия, чем ECa. Причина такого поведения кроется в том, что система стремится к равновесию, и при малейших отклонениях мембранного потенциала в сторону более отрицательных значений, чем EK, K+ будет двигаться по электрохимическому градиенту внутрь клетки, возвращая мембранный потенциал к равновесному потенциалу для калия.
Рисунок 3 | Диапазон возможных значений мембранного потенциала от ЕK до ECa (показан голубым цветом).
Величина потенциала покоя зависит от типа клеток и равна около –30 мВ в невозбудимых клетках и около –80 мВ в возбудимых клетках (нейроны, мышечные и эндокринные клетки). Когда мембранный потенциал более отрицателен, чем потенциал покоя, говорят, что мембрана гиперполяризована, а когда он приближается к нулю или даже принимает положительные значения, говорят о деполяризации мембраны.
В общем случае мембранный потенциал можно вычислить согласно уравнению Гольдмана-Ходжкина-Катца, которое принимает в расчет все основные катионы и анионы:
где E — мембранный потенциал; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура; F = 96485,55 Кл·моль–1 — константа Фарадея; PX — проницаемость мембраны для иона X; [C]in, out — равновесные концентрации ионов внутри и вне клетки. N.B.: для анионов внеклеточная концентрация стоит в знаменателе, а внутриклеточная — в числителе.
Что же обеспечивает проницаемость мембраны для ионов? Заряженные частицы не могут самостоятельно пересекать гидрофобный внутренний слой плазматической мембраны, и поэтому требуются специальные белки, образующие гидрофильную пору, через которую ионы могут двигаться через мембрану. Такие белки называются ионными каналами. Основной вклад в поддержание потенциала покоя вносят калиевые каналы семейств Kir (inward rectifying K+ channels — калиевые каналы внутреннего выпрямления) и K2P (two—pore domain K+ channels — калиевые каналы с двумя поровыми доменами, которые часто называют каналами утечки), а каналы других семейств могут обеспечивать быстрое изменение мембранного потенциала в возбудимых клетках. Каналы могут селективно пропускать определенный тип ионов, например, K+ (как каналы семейства Kir), или более широкий спектр веществ, как, например, коннексины — белки щелевых контактов.
Каналы бывают потенциал-зависимые (потенциал-управляемые), лиганд-зависимые, термо- и механочувствительные — в зависимости от стимула, который управляет открытием и закрытием канала. В роли стимула, таким образом, могут выступать изменения мембранного потенциала, химические агенты, температура, свет, механические и другие стимулы. Один и тот же канал может открываться под действием различных эндо- и экзогенных стимулов. Так, канал TRPV1 активируется повышением температуры более 43 °C[3], кислым pH[4] и разнообразными химическими веществами: капсаицином (алкалоид из перцев рода Capsicum)[3], эндоканнабиноидом анандамидом[5], окситоцином[6] и др.
Физиологическая роль каналов крайне важна. К примеру, мутации в генах, кодирующих белки ионных каналов, лежат в основе патогенеза многих заболеваний человека: некоторых видов эпилепсии[7], муковисцидоза[8], некоторых аритмий[9, 10] и др. Ионные каналы служат мишенями действия многих лекарств, ядов и токсинов.
Однако для формирования потенциала покоя недостаточно одних лишь каналов, ведь нужно создавать и поддерживать концентрационные градиенты на мембране. Основной механизм поддержания градиентов концентрации калия и натрия — это Na/K-АТФаза, фермент, за счет гидролиза одной молекулы АТФ переносящий три Na+ наружу и два K+ внутрь клетки. Она осуществляет электрогенный транспорт: в каждом транспортном цикле при переносе одного дополнительного положительного заряда наружу генерируется некоторая разность потенциалов на мембране. Чтобы оценить этот вклад Na/K-АТФазы в поддержание потенциала покоя, можно заблокировать работу фермента алкалоидом оубаином. Тогда мембрана деполяризуется примерно на 10 мВ[11].
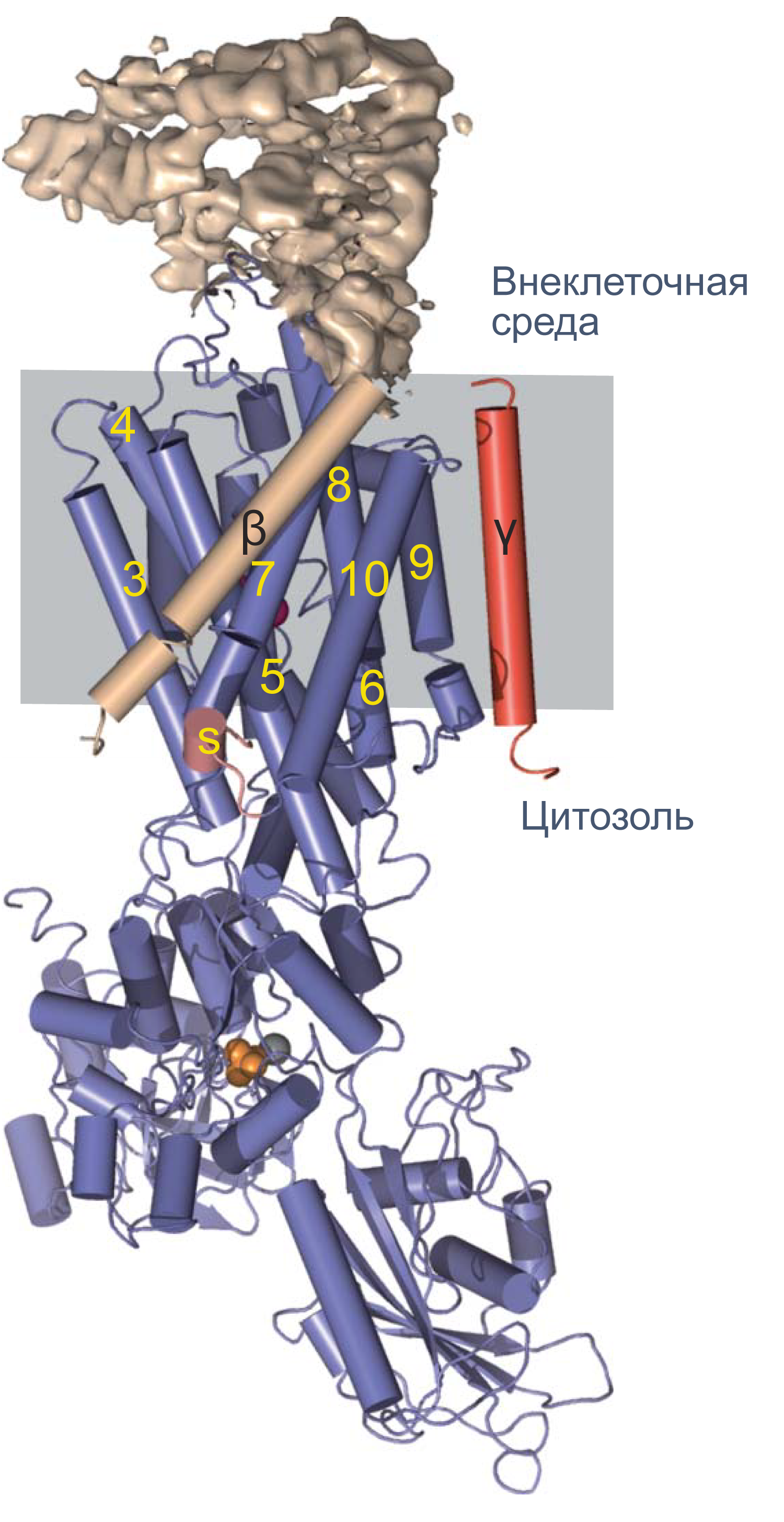
Рисунок 4 | Структура Na/K-АТФазы, полученная методом рентгеновской кристаллографии. Синим цветом показана α-субъединица, красным — γ-субъединица; β-субъединица показана бежевым цветом. Внеклеточная часть β-субъединицы показана в виде электронной плотности. Альфа-спирали изображены цилиндрами, бета-слои — плоскими стрелками[12].
Активный и пассивный транспорт веществ через мембрану
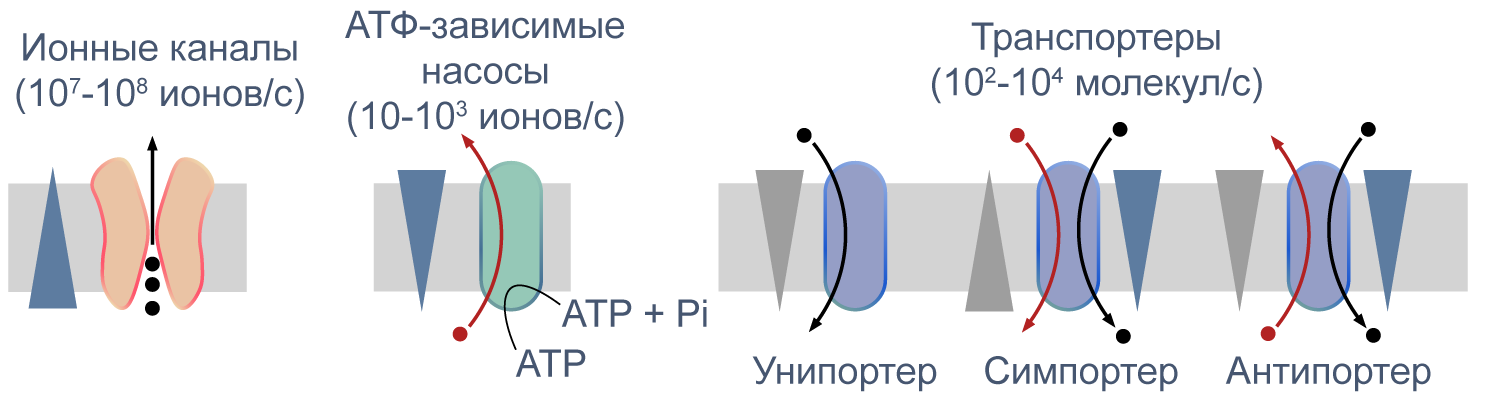
Процессы транспорта веществ через мембрану можно классифицировать по источнику энергии для транспорта. Пассивный транспорт — это движение вещества через канал или транспортер по градиенту концентрации*, то есть за счет энергии электрохимического градиента. Таким способом через калиевые каналы пассивно движутся ионы калия, или осуществляется перенос глюкозы через транспортер GLUT4 (такой тип транспорта еще называют облегченной диффузией, а транспортеры, переносящие только один субстрат — унипортерами). Кроме пассивного транспорта, существует активный транспорт, при котором субстраты переносятся против градиента концентрации с затратой энергии, запасенной клеткой в виде АТФ (например, Na/K-АТФаза).
Некоторые транспортеры сопрягают перенос ионов или молекул против градиента концентрации с движением ионов по градиенту концентрации. Симпортеры переносят различные частицы в одном направлении (например, KCC2 — K—Cl cotransporter 2 — K/Cl котранспортер 2), а антипортеры, или обменники, — в противоположных (например, NHE-1 — Na/H exchanger 1 — Na/H обменник, участвующий в поддержании клеточного pH). Такой транспорт называется вторично-активным.
Рисунок 5 | Пассивный и активный транспорт веществ через мембрану. Треугольниками показаны концентрационные градиенты. Черными стрелками показано движение по градиенту концентрации, красными — против градиента концентрации. По [13], с изменениями.
В старой литературе можно встретить концепцию «белков-переносчиков»: до открытия молекулярной идентичности многих каналов и транспортеров (т. е. какая молекула опосредует данный ионный ток и какой ген ее кодирует) существовало представление о переносчиках как о челноках, связывающих субстраты с одной стороны мембраны, диффундирующих через мембрану и высвобождающих субстраты с другой стороны. Однако, когда стали известны аминокислотные последовательности транспортных белков, стало понятно, что все они часто содержат многочисленные трансмембранные домены и образуют сквозной путь через мембрану.
Различия между каналами, транспортерами и насосами заключаются в механизме их работы и регуляции. Каналы представляют собой более или менее селективную пору, через которую ионы могут свободно диффундировать, не вызывая конформационных изменений в белке канала. При токе через отдельный канал в 1 пА по нему проходят 6×106 одновалентных ионов в секунду. Транспортер, связываясь с субстратом, изменяет свою конформацию для переноса субстрата. При ко-транспорте повышается аффинность транспортера в новой конформации к второму субстрату, и субстраты переносятся через мембрану сопряженно. Насосы, также называемые АТФазами, (ауто)фосфорилируются АТФ, и это фосфорилирование значительно изменяет их конформацию и приводит к транслокации субстратов через мембрану. Электрическая проводимость насосов очень мала: Na/K-АТФаза переносит всего около 300 Na+ и 200 K+ в секунду.
Граница между молекулами каналов и транспортеров не всегда строга. Например, семейство хлоридных каналов и транспортеров ClC (англ. Chloride Channel) включает в себя гомологичные друг другу каналы (ClC-1, 2, Ka и Kb) и Cl/H-обменники (ClC-3–7), которые можно превратить в каналы, внеся мутацию в единственный остаток глутамата (т. н. gating glutamate — воротный глутамат) [14]. Na/K-АТФазу также можно превратить в простую пору, например, с помощью палитоксина[15]. Хлоридный канал CFTR относится к группе ABC-транспортеров, однако он использует энергию АТФ не для транспорта ионов, а для регуляции открытия и закрытия канала[16]. Кроме того, существуют данные о том, что везикулярный транспортер глутамата VGLUT1 кроме обмена глутамата на протоны также опосредует не сопряженный с обменом ток Cl− [17].
Клеточная мембрана как электрическая цепь
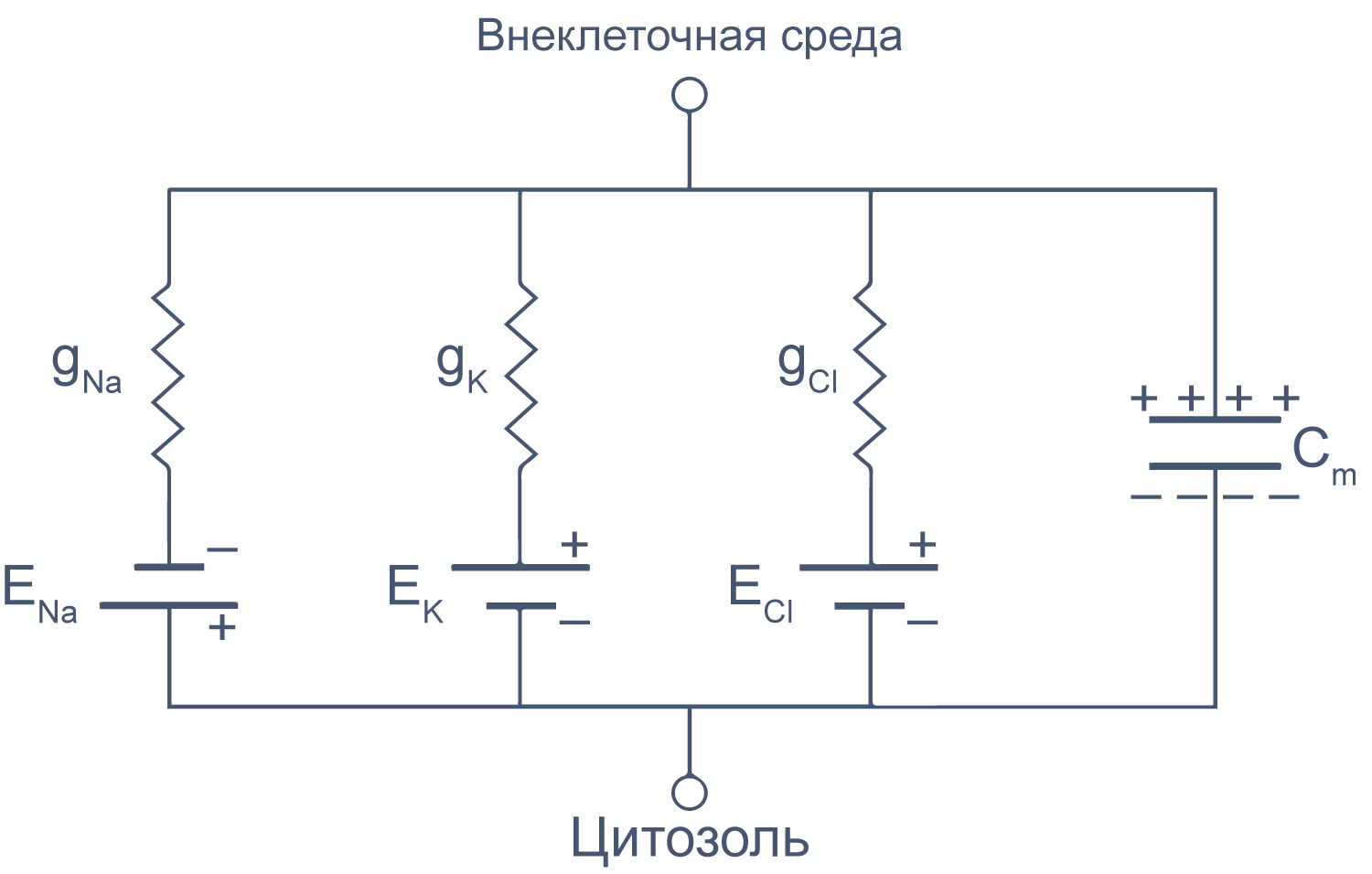
Липидный бислой мембраны можно представить как резистор (сопротивление) и конденсатор (емкость), соединенные параллельно. Величина сопротивления зависит от плотности каналов в мембране и их функционального состояния. Электроемкость возникает из-за разделения зарядов по обе стороны мембраны тонким слоем диэлектрика (гидрофобными хвостами фосфолипидов).
Рисунок 6 | Плазматическая мембрана, представленная в виде RC схемы. gNa, gK, gCl — проводимость** мембраны для ионов Na+, K+ и Cl–, соответственно; ENa, EK, ECl — электродвижущая сила, или равновесные потенциалы для соответствующих ионов, Сm — электроемкость мембраны.
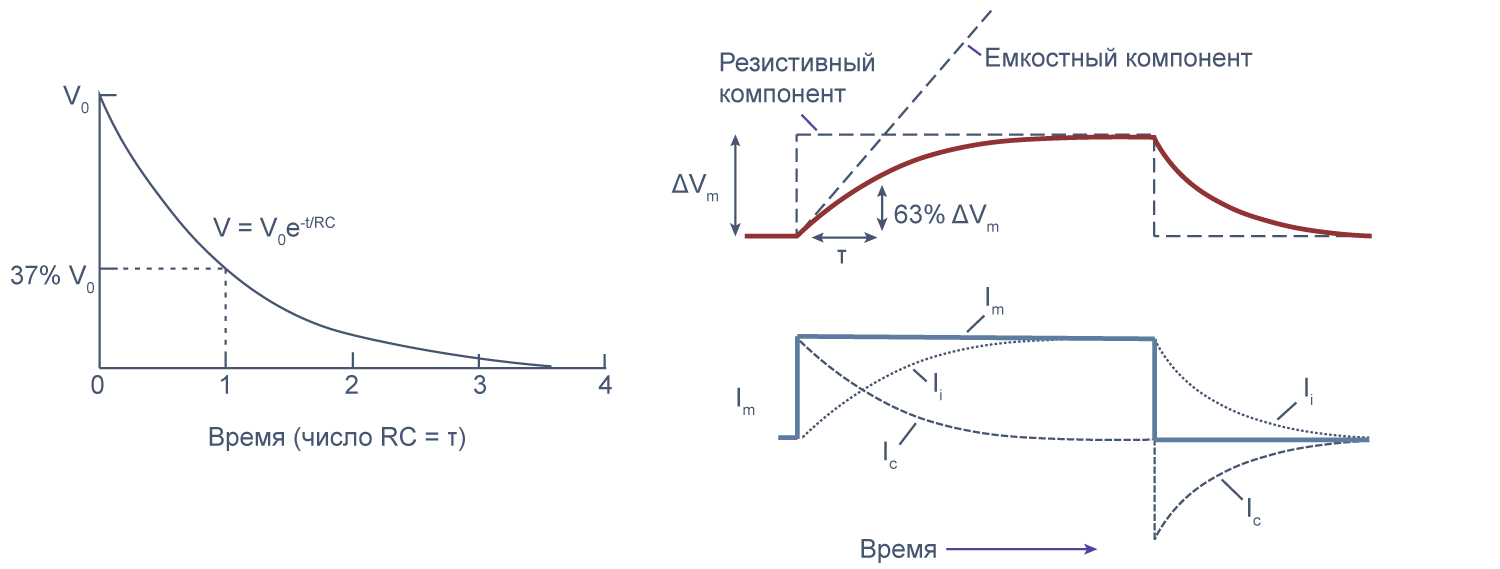
Можно считать, что проводимость (величина, обратная сопротивлению, измеряемая в сименсах) характеризует проницаемые для ионов компоненты структуры мембраны, а емкость — не проницаемые для ионов структуры. Удельная емкость мембраны составляет приблизительно 1 мкФ/см2 или 0,01 пФ/мкм2*** и мало зависит от типа клеток[2]. Это позволяет оценить размер клетки по ее электрическим характеристикам. Высокая электроемкость клеточных мембран задерживает изменения потенциала в ответ на ток. Эту задержку можно выразить через постоянную времени τ, которая равна произведению емкости и параллельно соединенного с ней сопротивления (RC). Если конденсатор зарядить на некоторую величину, а затем дать ему разрядиться через резистор, то потенциал будет убывать экспоненциально согласно формуле V = V0e–t/RC, то есть за каждые τ = RC секунд потенциал будет падать в 1/e раз (на 37 % от исходной величины). Этот расчет применим и к клеточной мембране: падение напряжения при разрядке мембраны будет подчиняться экспоненциальному закону. То есть, если приложить гипер- или деполяризующий стимул, то мембранный потенциал через время τ достигнет 63 % конечного сдвига.
Рисунок 7 | Падение напряжения при разрядке мембраны. Изменение мембранного потенциала при деполяризации мембраны на ΔVm [22], Ic — емкостный ток, Ii — ионный ток, Im — суммарный ток через мембрану. Пояснения в тексте.
Потенциал действия
Возбудимые клетки могут быстро изменять потенциал на мембране и этим запускать внутриклеточные процессы, например, мышечное сокращение или экзоцитоз везикул. Кратковременный локальный скачок мембранного потенциала от приблизительно –80 мВ (значения потенциала покоя) до 0…+20 мВ за счет изменения проницаемости мембраны для ионов называется потенциалом действия.
Для начала рассмотрим потенциал действия в аксонах нейрона на примере гигантского аксона кальмара. Выбор столь экзотического объекта обусловлен историческими причинами. Современная микроэлектродная техника — использование тонких стеклянных микропипеток, заполненных раствором электролита, — была предложена лишь в 1949 году Дж. Лингом и Р. Джерардом[18]. До этого поместить электрод, представлявший собой тонкую проволоку, внутрь клетки, не разрушив ее, можно было только в случае ее крупных размеров. Гигантский аксон кальмара стал идеальным модельным объектом для изучения потенциала действия: его диаметр может достигать 0,5–1 мм. Этот отросток служит для быстрой передачи нервных импульсов у беспозвоночных, у которых отсутствует миелинизация. Внутренним содержимым аксона легко манипулировать, заменяя ионный состав внутриклеточного раствора, а внутрь такого аксона можно поместить электрод для регистрации мембранного потенциала.
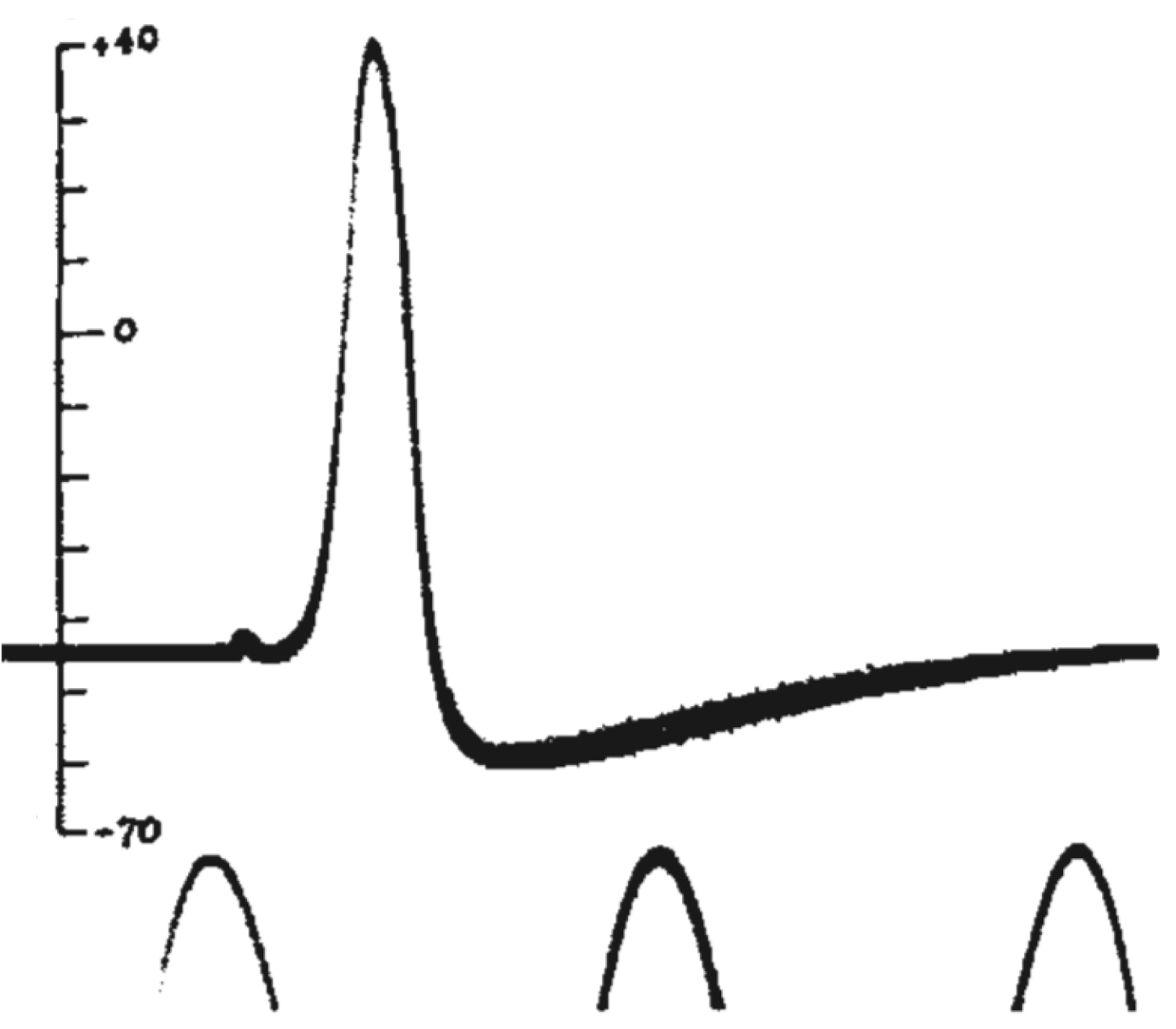
Так, в 1939 году А. Ходжкин и Э. Хаксли опубликовали в журнале Nature короткую заметку «Потенциалы действия, зарегистрированные внутри нервного волокна»[19], в которой они описали первый эксперимент по внутриклеточному измерению мембранного потенциала на гигантском аксоне кальмара. Посмотрим на потенциалы действия, которые зарегистрировали исследователи.
Рисунок 8 | Потенциал действия из статьи А. Ходжкина и Э. Хаксли 1939 года[19]. Потенциал действия был зарегистрирован как разность потенциала между внутренней средой аксона и внешней средой. Пики внизу рисунка — это фрагменты синусоидального сигнала с частотой 500 Гц. Вертикальной чертой отмечен потенциал внутреннего электрода в милливольтах, потенциал морской воды снаружи аксона был принят за ноль.
Мы видим резкую деполяризацию мембраны до положительных значений, а затем более плавное возвращение потенциала к отрицательным значениям, зачастую более отрицательным, чем величина потенциала покоя. Из этих наблюдений следовало два важных вывода: 1) потенциал действия генерируется мембраной клетки, что не было очевидно в 1930-е годы; 2) поскольку измеренная амплитуда потенциала действия была больше величины мембранного потенциала, генерация потенциала действия — это активный процесс, который нельзя объяснить временным «пробоем» в мембране (каким бы наивным такое представление нам не казалось сегодня, в 1930-е так думали многие физиологи). В том же году К. С. Коул и Х. Дж. Кертис[20] зарегистрировали кратковременное изменение проводимости мембраны с 1 мСм/см2 до 40 мСм/см2 при генерации потенциала действия. Эти данные также свидетельствовали о тонкой регуляции этого процесса.
После Второй мировой войны Ходжкин и Хаксли вернулись к своим исследованиям. В 1945 году они опубликовали статью с несколькими дополнительными экспериментами, подтверждающими сформулированные ранее выводы. Но и тогда ионные механизмы потенциала действия оставались неясными.
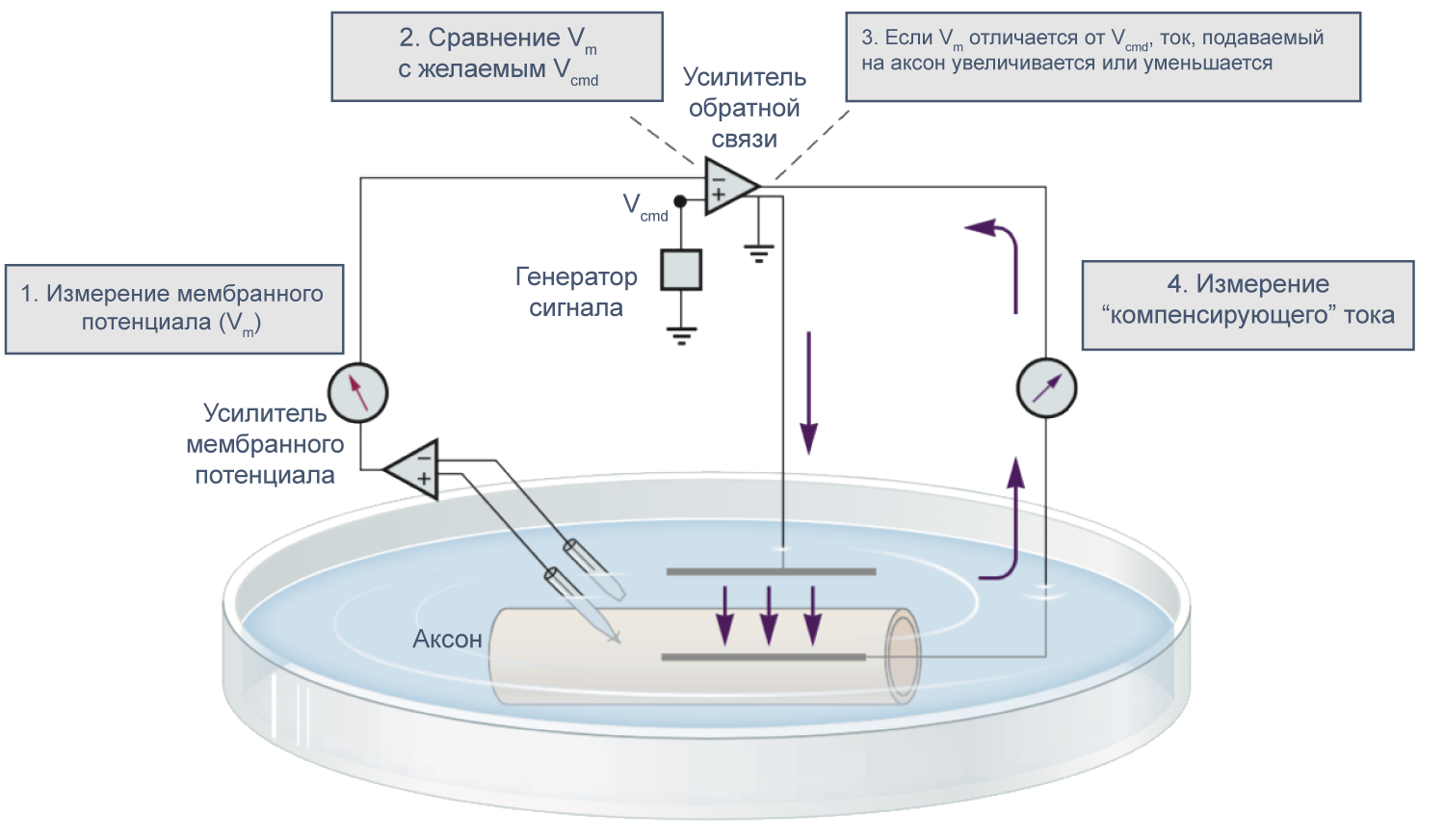
В 1952 году вышла серия статей, посвященных разгадке механизма генерации потенциала действия. Ведущую роль в этом открытии сыграл новый метод фиксации потенциала с помощью двух электродов (в англоязычной литературе TEVC — two-electrode voltage clamp), разработанный в конце 1940-х годов К. С. Коулом и Дж. Мармонтом[21]. Этот метод позволяет измерять не только потенциал, но и токи при заданном значении мембранного потенциала. Как же осуществляется фиксация потенциала с помощью двух электродов на заданном уровне (Vcmd — «командный потенциал»)? В клетку помещают два электрода, один из которых измеряет потенциал (относительно внеклеточного электрода сравнения) и передает его значение на специальный усилитель, который сравнивает измеренный потенциал со значением командного потенциала. Это устройство вычисляет ток, необходимый для компенсации этой разницы, и подает через второй внутриклеточный электрод ток такой величины, чтобы потенциал на мембране клетки стал равен Vcmd (Vm = Vcmd). Из амплитуды тока, необходимого для компенсации сдвига потенциала до Vcmd, можно сделать вывод о токе через мембрану при данном значении мембранного потенциала. Ток при данном значении потенциала равен току, подаваемому на второй электрод, взятому с обратным знаком.
Рисунок 9 | Схема фиксации потенциала с помощью двух электродов[21].
В 1970–80-х годах Эрвин Неер и Берт Сакман (Erwin Neher, Bert Sakmann) предложили метод локальной фиксации потенциала (англ. patch clamp), позволяющий работать с мелкими клетками и токами малой амплитуды и даже регистрировать активность отдельных каналов. Тем не менее, метод фиксации потенциала двумя электродами в микроэлектродной конфигурации используется и сегодня при работе с такими крупными клетками, как ооциты лягушки Xenopus laevis.
Временной ход потенциала действия
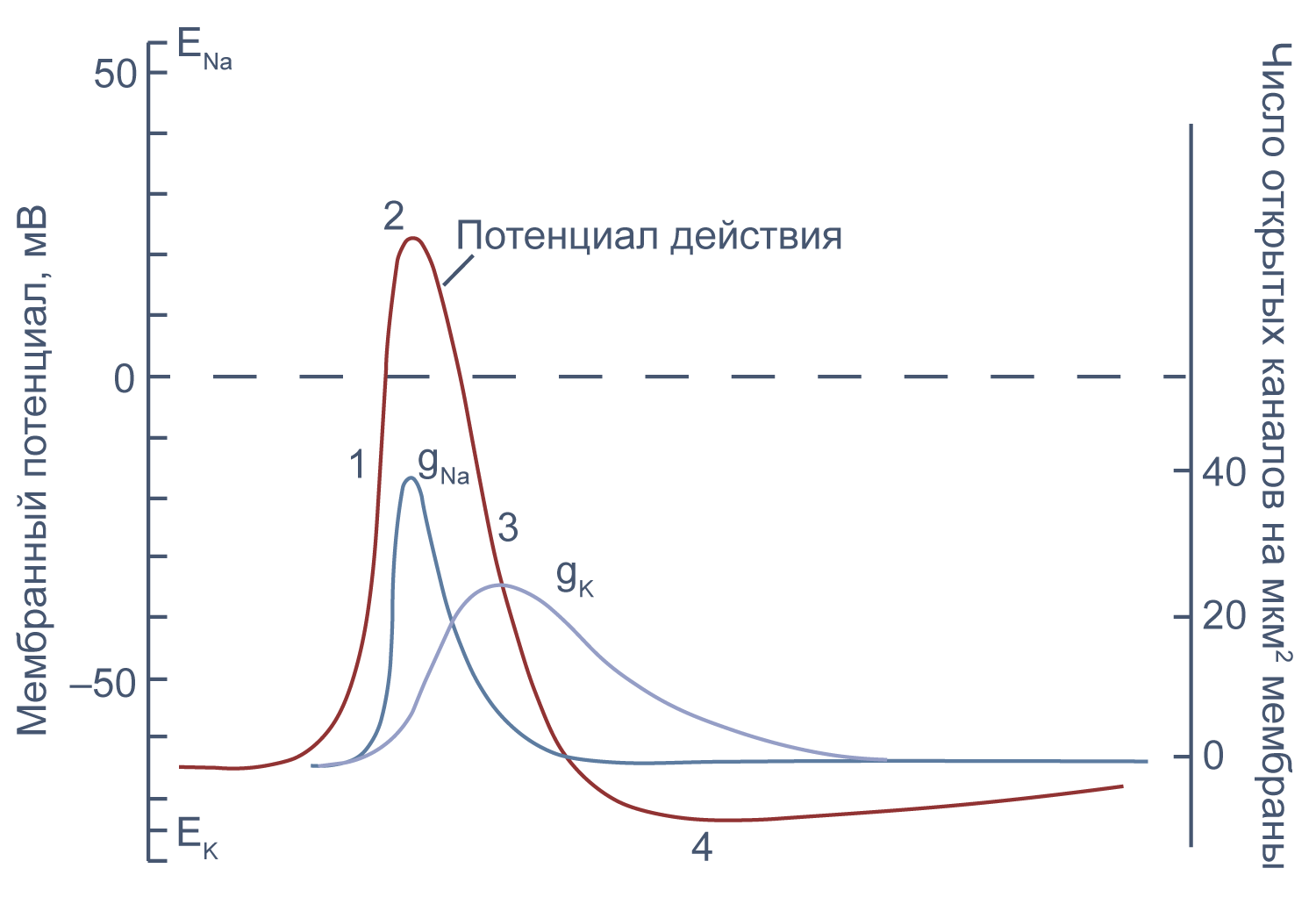
Потенциал действия в аксоне можно разделить на 1) фазу быстрой деполяризации до 2) положительных значений (овершута, от англ. overshoot), 3) фазу реполяризации, в которой потенциал возвращается к потенциалу покоя или даже до несколько более отрицательных значений — 4) следовая гиперполяризация.
Рисунок 10 | Потенциал действия и изменения проводимости мембраны для Na+ и K+ в гигантском аксоне кальмара. Из [22], с изменениями.
Изменяя ионный состав внутри- и внеклеточного раствора, можно изолировать ионные токи, которые опосредуют изменение мембранного потенциала при потенциале действия. Так, помещая аксон в раствор, в котором натрий заменен на холин, можно изолировать натриевый и калиевый компонент потенциала действия, то есть отдельно измерить калиевый ток[20]. Этого же можно достичь применением блокаторов потенциал-зависимых натриевых и калиевых каналов — тетродотоксина и тетраэтиламмония (TEA).
Чтобы понять взаимосвязь ионных токов и вызванных ими изменений потенциала, рассмотрим всю цепь событий при генерации потенциала действия. Сначала мембрана деполяризуется под действием внешнего стимула: поступления в клетку катионов через лиганд-управляемые каналы, закрытия калиевых каналов или электрической стимуляции в эксперименте. Если деполяризация достигает порогового значения для потенциалзависимых натриевых каналов (Nav), они открываются, натрий по градиенту своей концентрации входит в клетку, и мембрана деполяризуется еще сильнее. Дальнейшая деполяризация влечет за собой лавинообразное открытие все новых натриевых каналов, ток через которые приводит к еще большей деполяризации. Однако эта петля положительной обратной связи не работает бесконечно: открывшись на некоторое время, натриевые каналы инактивируются и не могут открыться вновь, пока мембранный потенциал не вернется к отрицательным значениям.
Механизм инактивации был предложен еще в математической модели Ходжкина и Хаксли[23] на основании кинетических характеристик тока. Они предположили, что в натриевом канале есть три активационные частицы m и одна инактивационная частица h. Когда стала известна аминокислотная последовательность канала, выяснилось, что канал на самом деле имеет четыре гомологичных активационных домена и один инактивационный, однако один из активационных доменов срабатывает значительно медленнее остальных трех, и его влияние на кинетические характеристики тока маскируется происходящей в то же время инактивацией канала (например, [24]).
В то же время деполяризация мембраны приводит к активации потенциал-зависимых калиевых каналов (Kv), которые открываются медленнее, чем натриевые, калий выходит из клетки, и потенциал возвращается к потенциалу покоя и может даже временно стать более отрицательным: пока натриевые каналы инактивированы, потенциал становится ближе к калиевому равновесному потенциалу, и это явление называется следовой гиперполяризацией.
Генерация потенциала действия происходит по принципу «все или ничего». Если деполяризующий стимул не достиг порогового значения, потенциал действия не генерируется. Если же порог был достигнут, положительная обратная связь обеспечивает открытие всех доступных натриевых каналов, и потенциал действия достигает своей максимальной амплитуды.
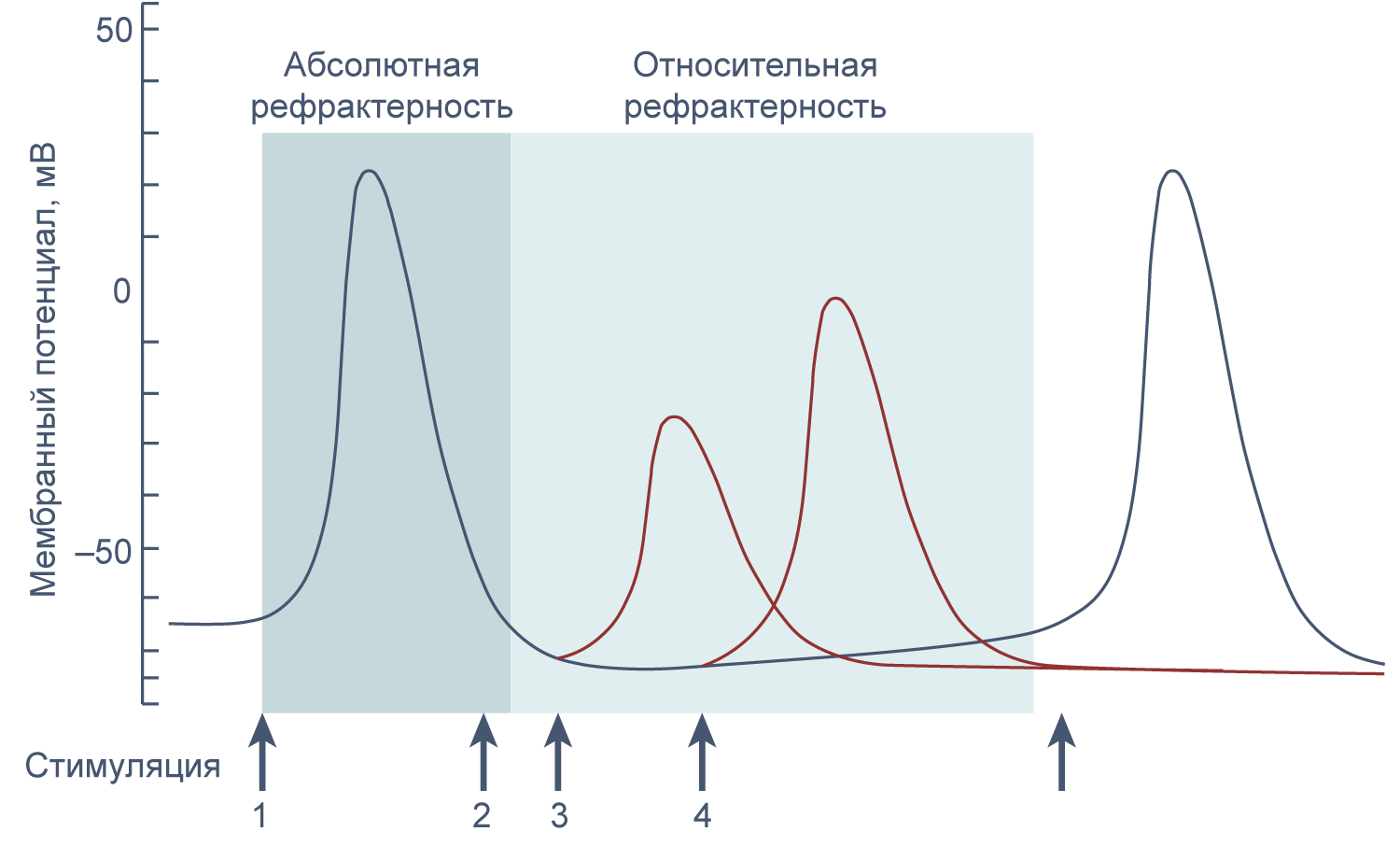
Если новый стимул приходит во время или сразу после генерации потенциала действия, второй потенциал действия не возникает или обладает меньшей амплитудой, чем первый. Это явление называется рефрактерностью. Стимул, возникший в период абсолютной рефрактерности, не вызывает генерации потенциала действия, а пришедшийся на период относительной рефрактерности вызывает потенциал действия уменьшенной амплитуды, так как часть натриевых каналов все еще инактивирована.
Рисунок 11 | Абсолютная и относительная рефрактерность. Стимуляция в период абсолютной рефрактерности (2) не ведет к генерации потенциала действия, а стимуляция в период относительной рефрактерности (3 и 4) приводит к генерации потенциала действия сниженной амплитуды.
Стоит отметить, что внутриклеточная концентрация физиологически значимых ионов при генерации потенциала действия не меняется, и ионные токи задействуют пренебрежимо малую долю от общего числа Na+ и K+. Это можно проиллюстрировать следующим примером. Рассчитаем число ионов, которое должно пересечь мембрану для деполяризации на 100 мВ. Заряд на мембране равен произведению емкости мембраны и потенциала: Q = CmVm. Удельная емкость мембраны близка к 1 мкФ/см2, а сдвиг потенциала в нашем случае равен 0,1 В. Тогда количество разделенных зарядов равно Q = 10−6 Ф/см2 × 0,1 В = 10−7 Кл/см2. Величина заряда одного иона Na+ или K+ (элементарного заряда) равна 1,6 × 10−19 Кл, тогда количество переносимых через мембрану ионов равно 10−7 Кл/см2 / 1,6 × 10−19 Кл = 6,25 × 1011 ионов/см2, или 6250 ионов/мкм2. Для клетки диаметром 10 мкм площадь поверхности мембраны будет приблизительно равна 4πr2 = 314 мкм2 (в этом расчете для простоты мы считаем клетку гладкой сферой), а объем — 4πr3/3 = 524 мкм3. При внутриклеточной концентрации Na+ 10 мМ, а K+ 150 мМ содержание этих ионов в цитозоле будет равно 3,2 × 109 и 4,7 × 1010 соответственно. В течение одного потенциала действия приблизительно 314 мкм2 × 6,250 ионов/мкм2 ≈ 2 000 000 ионов Na+ входит в клетку в фазе деполяризации и примерно столько же ионов K+ выходит из клетки в фазе реполяризации, что составляет всего 0,06 % от общего числа ионов натрия в клетке. Токи такой величины обычно не изменяют макроскопические концентрации ионов в клетке, поскольку работа Na/K-АТФазы компенсирует эти незначительные изменения. Однако при определенных условиях концентрации Na+ и K+ все же могут измениться, например, при продолжительной стимуляции аксонов с малым диаметром[25].
Распространение возбуждения по аксону
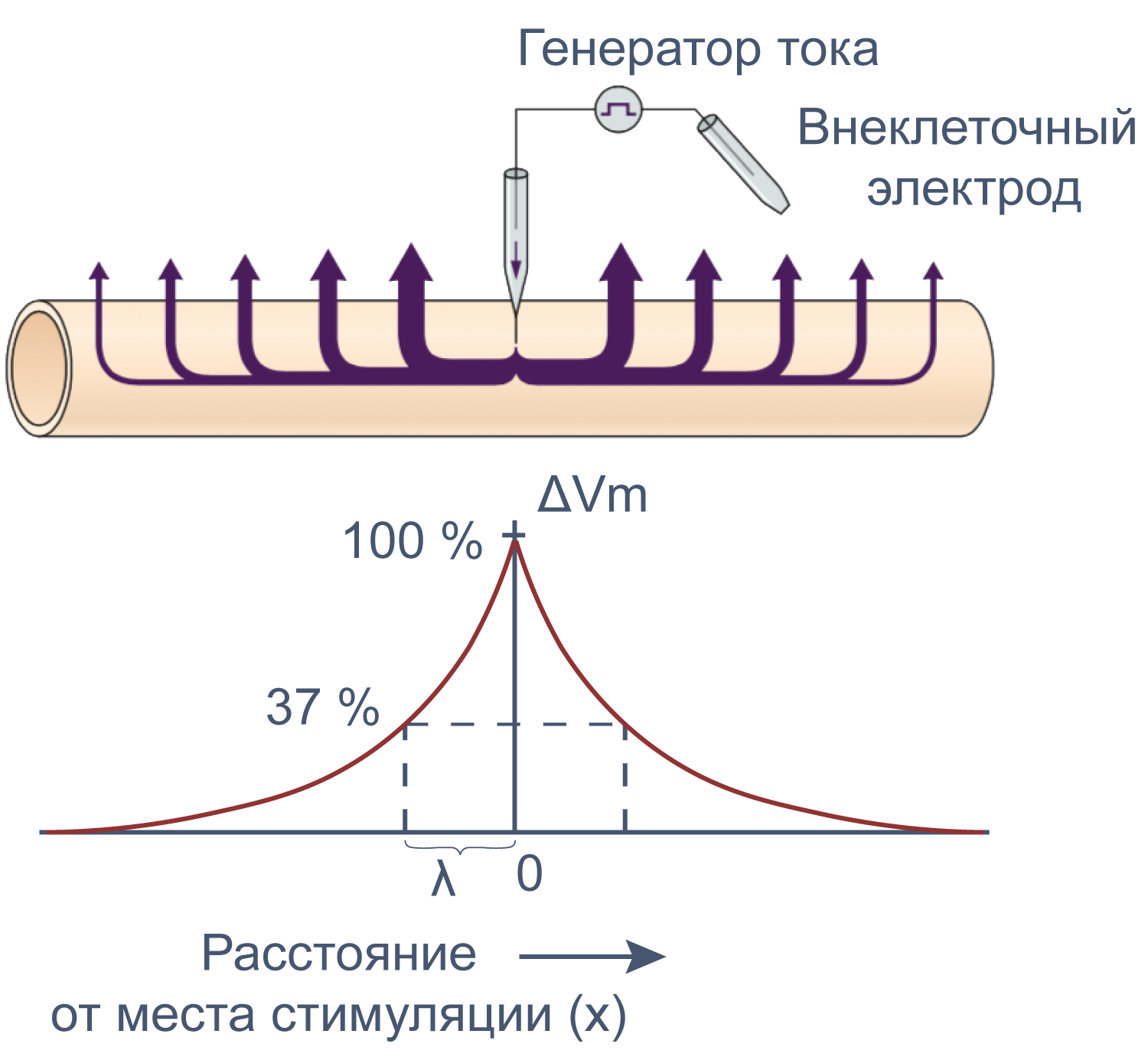
Электрические свойства мембраны помогают понять изменения мембранного потенциала не только во времени, но и в пространстве. Пассивное, или электротоническое распространение возбуждения по мембране происходит без изменения проводимости потенциал-зависимых каналов. Для распространения потенциала действия важен как активный (изменение проводимости натриевых и калиевых каналов), так и пассивный механизмы, поскольку деполяризация, вызывающая открытие новых потенциал-зависимых натриевых каналов, должна достигнуть нового невозбужденного участка аксона, и происходит это благодаря электротоническому распространению возбуждения.
Рисунок 12 | Электротоническое распространение возбуждения. Пояснения в тексте [22].
Сдвиг потенциала в точке, отстоящий на x от места стимуляции, можно вычислить как Ex = E0e–x/λ, где E0 — это сдвиг потенциала в точке стимуляции, а λ — постоянная длины.
Постоянная длины возрастает с увеличением сопротивления мембраны (rm) и уменьшается с возрастанием сопротивления аксоплазмы (ri), которое в свою очередь зависит от концентрации подвижных зарядов в объеме аксона. Знание этих закономерностей позволяет понять зависимость скорости распространения возбуждения от радиуса (R) аксона. Сопротивление мембраны rm пропорционально 1/2πR, сопротивление аксоплазмы ri — 1/πR2, а емкость мембраны Cm пропорциональна R. По мере увеличения радиуса аксона и rm, и ri уменьшаются, но ri уменьшается сильнее. Постоянная длины увеличивается, следовательно, сдвиг потенциала может распространяться по более крупному аксону дальше. Кроме того, увеличение радиуса аксона ведет к увеличению емкости мембраны, однако этот эффект нивелируется тем, что емкость с увеличением радиуса растет линейно, а уменьшение ri пропорционально квадрату радиуса. Таким образом, проводимость аксоплазмы увеличивается быстрее (при снижении ri), чем растет емкость мембраны, и это позволяет току быстрее достигать невозбужденных участков мембраны более крупного аксона.
Зависимость скорости распространения потенциала действия по аксону от его диаметра объясняет необходимость в гигантских аксонах у кальмара. Однако у позвоночных гигантских аксонов нет, и достаточная скорость проведения нервных импульсов достигается с помощью миелинизации аксонов. Миелиновые оболочки образованы специальными глиальными клетками: олигодендроцитами в центральной нервной системе и клетками Шванна в периферической. Эти клетки оборачивают аксон, образуя вокруг него плотный чехол из десятков слоев плазматической мембраны, который работает как изолятор. Под миелиновой оболочкой очень мало или почти нет натриевых каналов. Они оказываются расположены на небольших участках мембраны аксона между двумя соседними шванновскими клетками или олигодендроцитами — в перехватах Ранвье. Миелиновая оболочка увеличивает скорость проведения потенциала действия благодаря повышению сопротивления мембраны rm. При этом снижаются потери тока через мембрану, и деполяризация может пассивно распространяться на бо́льшие расстояния. Кроме того, из-за снижения емкости мембраны Cm, меньшая доля тока тратится на перезарядку мембраны. Миелинизация делает передачу потенциала действия не только быстрее, но и эффективнее, поскольку натриевые каналы располагаются только в перехватах Ранвье, благодаря чему меньшее количество ионов натрия входит в клетку и меньше энергии требуется на работу Na/K АТФ-азы для поддержания концентрационного градиента.
Потенциалы действия в других возбудимых клетках
Минималистичный натриево-калиевый потенциал действия характерен только для аксонов нейронов. В других частях нейрона и в иных типах возбудимых клеток в генерации потенциала действия принимают участие разнообразные ионные каналы, в том числе калиевые каналы других семейств и кальциевые каналы плазматической мембраны и эндоплазматического ретикулума (ЭПР является внутриклеточным депо кальция; общая концентрация Ca2+ в нем достигает миллимолярных значений, а концентрация свободного кальция находится в микромолярном диапазоне[26]; эти значения на несколько порядков выше, чем 100 нМ свободного Ca2+ в цитозоле в состоянии покоя). Различия в экспрессии генов ионных каналов в различных типах возбудимых клеток порождают разнообразие потенциалов действия, различающихся ионными механизмами, длительностью (от 1,5 мс в аксонах до 500 мс в кардиомиоцитах желудочков), необходимостью внешнего стимула для генерации или наличием собственного ритма. Многие ионные каналы, не участвуя напрямую в генерации потенциала действия, влияют на возбудимость клеток и таким образом вносят вклад в разнообразие электрической активности клеток.
* Принятое в физиологической литературе употребление фраз «по» или «против градиента концентрации» расходится с физическим понятием градиента. В математике и физике градиент направлен в сторону наибольшей скорости возрастания функции или величины; так, если вещество движется в направлении этого вектора, то физиологи говорят о движении «против градиента концентрации», а если в противоположном направлении — то «по градиенту концентрации». Такое словоупотребление прочно закрепилось в литературе, но пусть оно не сбивает вас с толку, когда вы размышляете, откуда взялся минус перед градиентом концентрации в уравнении диффузионного потока (уравнении Фика): J = — D dC/dx, где J — диффузионный поток [моль∙см-2∙с-1], D — коэффициент диффузии [см2∙с-1], а dC/dx— градиент концентрации.
** Проводимость (g = 1/R) — это характеристика скорости движения любых зарядов через мембрану, а проницаемость (P) отражает, насколько легко частицы могут двигаться через мембрану независимо от того, движутся они или нет. Для ионов эти величины связаны. Например, в фазе быстрой деполяризации при потенциале действия возрастает как проводимость, так и проницаемость мембраны для ионов натрия. Однако зачастую, если проницаемость канала для какого-то иона высока из-за высокого сродства участков поры канала для этого иона, такие ионы будут двигаться через канал медленнее, и проводимость будет ниже, чем для других ионов, для которых канал менее проницаем.
*** Удельная емкость чистого липидного бислоя составляет около 0,8 мкФ/см2, разница между электроемкостью мембраны и липидного бислоя возникает из-за обилия встроенных в мембрану белков.
Библиография
- Hediger M.A. et al. The ABCs of membrane transporters in health and disease (SLC series): Introduction // Mol. Aspects Med. 2013. Vol. 34. P. 95–107.
- Hille B. Ion Channels of Excitable Membranes. Third edit. Sinauer Associates, Inc., 2001.
- Caterina M.J. et al. The capsaicin receptor: A heat-activated ion channel in the pain pathway // Nature. 1997. Vol. 389, № 6653. P. 816–824.
- Jordt S.-E., Tominaga M., Julius D. Acid potentiation of the capsaicin receptor determined by a key extracellular site // Proc. Natl. Acad. Sci. 2000. Vol. 97, № 14. P. 8134–8139.
- Smart D. et al. The endogenous lipid anandamide is a full agonist at the human vanilloid receptor (hVR1) // Br. J. Pharmacol. 2000. Vol. 129, № 2. P. 227–230.
- Nersesyan Y. et al. Oxytocin Modulates Nociception as an Agonist of Pain-Sensing TRPV1 // Cell Rep. 2017. Vol. 21, № 6. P. 1681–1691.
- Berkovic S.F. et al. Human epilepsies: interaction of genetic and acquired factors // Trends Neurosci. 2006. Vol. 29, № 7. P. 391–397.
- Welsh M.J., Smith A.E. Molecular mechanisms of CFTR chloride channel dysfunction in cystic fibrosis // Cell. 1993. Vol. 73, № 7. P. 1251–1254.
- Ruan Y., Liu N., Priori S.G. Sodium channel mutations and arrhythmias // Nat. Rev. Cardiol. 2009. Vol. 6, № 5. P. 337–348.
- Giudicessi J.R., Ackerman M.J. Potassium-channel mutations and cardiac arrhythmias — Diagnosis and therapy // Nat. Rev. Cardiol. Nature Publishing Group, 2012. Vol. 9, № 6. P. 319–332.
- Thomas R.C. Electrogenic sodium pump in nerve and muscle cells // Am. J. Physiol. 1972. Vol. 52, № 3. P. 563–594.
- Morth J.P. et al. Crystal structure of the sodium-potassium pump // Nature. 2007. Vol. 450, № 7172. P. 1043–1049.
- Lodish H. et al. Molecular Cell Biology (5th edition) // Biochemistry and Molecular Biology Education. 2003.
- Scheel O. et al. Voltage-dependent electrogenic chloride/proton exchange by endosomal CLC proteins // Nature. 2005. Vol. 436, № 7049. P. 424–427.
- Artigas P., Gadsby D.C. Ouabain affinity determining residues lie close to the Na/K pump ion pathway. // Proc. Natl. Acad. Sci. U. S. A. 2006. Vol. 103, № 33. P. 12613–12618.
- Li, C., Ramjeesingh, M., Wang, W., Garami, E., Hewryk, M., Lee, D., Rommens, J. M., Galley, K., Bear, C. E. ATPase Activity of the Cystic Fibrosis Transmembrane Conductance Regulator // Journal of Biological Chemistry. 1996. № 45 (271). P. 28463–28468.
- Martineau M. et al. VGLUT1 functions as a glutamate/proton exchanger with chloride channel activity in hippocampal glutamatergic synapses // Nat. Commun. Springer US, 2017. Vol. 8, № 1.
- Ling G., Gerard R.W. The normal membrane potential of frog sartorius fibers // J. Cell. Comp. Physiol. Wiley-Blackwell, 1949. Vol. 34, № 3. P. 383–396.
- Hodgkin A.L., Huxley A.F. Action potentials recorded from inside a nerve fibre // Nature. 1939. Vol. 144. P. 710–711.
- Cole K.S., Curtis H.J. Electric Impedance of the Squid Giant Axon During Activity // J. Gen. Physiol. 1939. Vol. 22, № 5. P. 649–670.
- Cole K.S. Mostly membranes // Annu. Rev. Physiol. 1979. Vol. 41, № 1. P. 1–24.
- Kandel E.R. et al. Principles of Neural Science. Fifth Edit. The McGraw-Hill Companies, Inc., 2013. 1709 p.
- Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve // J. Physiol. 1952. Vol. 117. P. 500–544.
- Capes D.L. et al. Domain IV voltage-sensor movement is both sufficient and rate limiting for fast inactivation in sodium channels // J. Gen. Physiol. 2013. Vol. 142, № 2. P. 101–112.
- http://www.physiologyweb.com/lecture_notes/neuronal_action_potential/neuronal_action_potential_na_and_k_concentrations_do_not_change_during_an_action_potential.html
- Bygrave F.L., Benedetti A. What is the concentration of calcium ions in the endoplasmic reticulum? // Cell Calcium. Churchill Livingstone, 1996. Vol. 19, № 6. P. 547–551.
Нашли опечатку? Выделите фрагмент и нажмите Ctrl+Enter.
Вы в первый раз на нашем сайте?
Для входа нужно использовать логин и пароль от личного кабинета ВУЗа http://www.kstu.ru/ds/eu_21.jsp?id=0
На данном сайте ваши пароли не хранятся, т.к. используется единая система управления доступом ВУЗа (LDAP-сервер), Менять пароли и восстанавливать нужно через личный кабинет http://www.kstu.ru/ds/eu_21.jsp?id=0
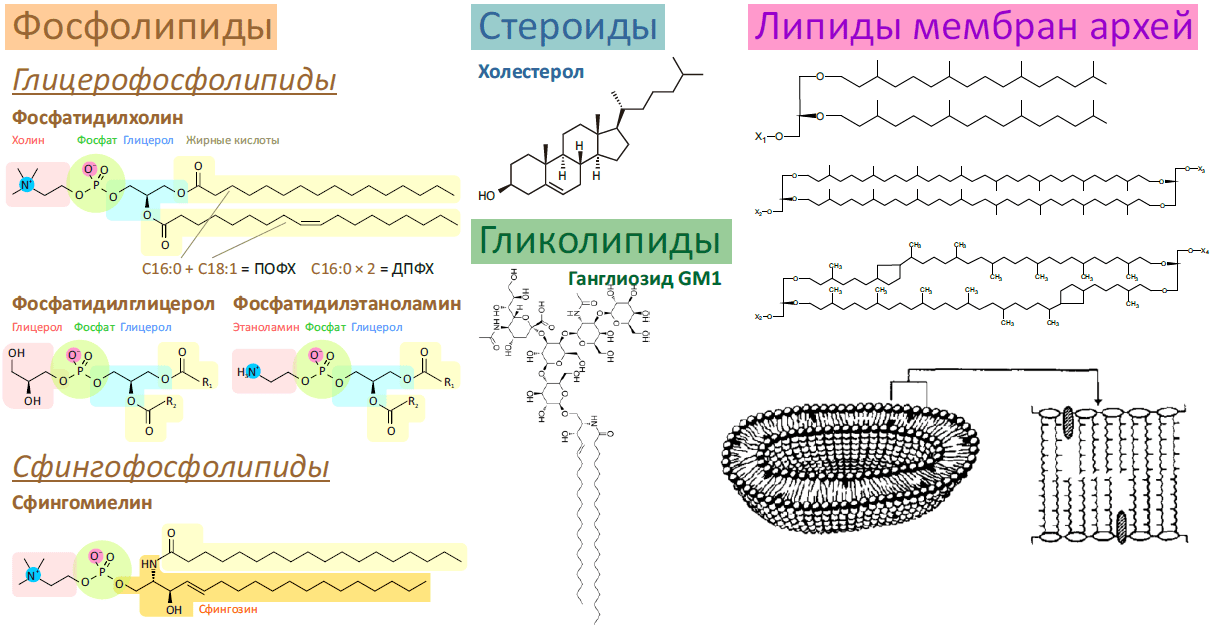
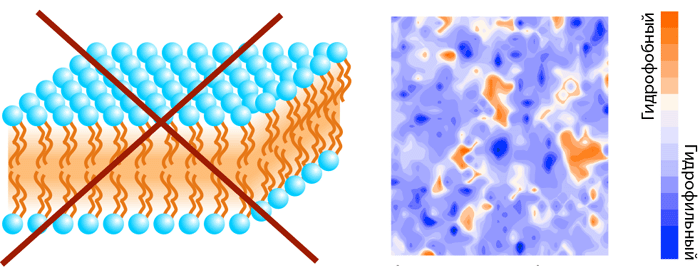
Жизнь в том виде, в каком мы ее знаем, невозможно представить без биомембраны, разделяющей «внутренний мир» клетки и всё остальное пространство. Мембрана обеспечивает взаимодействие клетки с внешней средой, избирательно пропуская многие вещества, а также является средой протекания множества биохимических процессов. И хотя большую часть полезной работы выполняют белки, которыми мембрана буквально «нашпигована», роль липидного матрикса не стоит недооценивать. Липиды — это не просто «океан», в котором плавают белки. Это «умный» океан, чьи физико-химические свойства были тщательно подобраны в ходе эволюции так, чтобы создать эффективную платформу для функционирования и взаимодействия мембранных белков.
Вопрос зарождения жизни на Земле вряд ли когда-нибудь получит окончательный ответ, но мало кто сомневается в том, что само ее появление стало возможным лишь в тот момент, когда в «первичном бульоне» (так в биологии принято называть растворенные в доисторическом мировом океане простые органические вещества) стали появляться маленькие изолированные области пространства, ставшие основной ареной для эволюции. В этих «первичных клетках» биохимические процессы могли протекать существенно быстрее, нежели на безбрежных просторах океана, и такое разделение является одной из предпосылок для первых, добиологических, шагов эволюции. Один из теоретиков абиотического происхождения жизни на Земле — академик А.И. Опарин — представлял себе эти «первичные клетки» в виде коацерватов (свободно плавающих липидных пузырьков, внутри которых протекала химическая эволюция). Согласно некоторым современным воззрениям, жизнь могла зародиться в гидротермальных источниках, где «первичная клетка» была образована минеральными отложениями [1]. Так или иначе, именно компартментализация (этим сложным словом обозначают обособленность содержимого клетки от внешней среды, а также подразделение самих клеток на внутренние «отсеки») является одним из непреложных признаков жизни.
Краткая история исследования липидов и биомембран
Структурообразующую функцию биологических мембран выполняют липиды — амфифильные молекулы, имеющие полярную головку и неполярный (гидрофобный) хвост. Они малорастворимы в воде и склонны к образованию моно- и бимолекулярных слоев благодаря своей амфифильной природе. Еще из школьного курса биологии известно, что мембрана состоит из двойного слоя (бислоя) липидов, «прячущих» от воды внутрь гидрофобные и выставляющих на поверхность полярные (гидрофильные) части [2].
Любопытно, что одним из первых исследователей свойств липидов стал один из «отцов-основателей» США Бенджамин Франклин, который в 1773 году провел серию экспериментов по измерению площади масляных пятен на поверхности пруда, остающихся от ложки (5 мл) растекающегося оливкового масла: пятна неизменно оказывались размером ≈2000 м2. Если бы любознательный сэр имел в то время представление о молекулярном строении вещества, он легко мог бы вычислить площадь, приходящуюся на одну молекулу (!) триглицерида олеиновой кислоты (основного компонента оливкового масла) в этом мономолекулярном пятне, и, причем, довольно точно:
где Mr — масcа 1 моля триолеина, NA — число Аводгадро, Sпятна — площадь пятна, Vложки — объем ложки, ρмасла — плотность масла. В результате мы получим значение площади Sмол ≈ 1 нм2 (на молекулу). Несложно оценить и толщину мономолекулярного слоя, равную размеру одной молекулы триолеина, разделив Vложки на Sпятна — 2,5 нм.
Более ста лет спустя, Чарльз Овертон заметил, что через биомембраны сравнительно легко проникают вещества, хорошо растворимые в липидах, из чего он сделал заключение, что мембрана должна быть образована тонким липидным слоем. Так эксперименты Франклина оказались впереди современных биофизических изысканий. 1925-м годом датируется идея бислойности мембраны: Гортер и Грендель обнаружили, что монослой липидов, выделенных из мембран эритроцитов, ровно вдвое превосходит площадь поверхности самих клеток.
Однако тогда же было замечено, что мембрана содержит значительное количество белков, которые сильно влияют на ее свойства (в частности, поверхностное натяжение). Это открытие повлекло появление концепции мембраны-«сендвича» (Доусон и Доннелли, 1935), согласно которой липидный бислой, как слой масла в бутерброде, заключен между двумя слоями белка. Прошло не одно десятилетие, пока точные данные по соотношению белков и липидов в мембранах различных клеток и современные методы исследования (такие как рентгеноструктурный анализ и электронная микроскопия) не доказали ошибочности этого представления: на самом деле, белки не окружают бислой, — они в него «встроены», подобно элементам мозаики.
Эта метафора дала название последней «классической» теории строения мембраны: «жидкостно-мозаичная мембрана» [3]. Согласно этой теории, мембрана представляет собой липидный «океан», в котором, подобно айсбергам, плавают молекулы мембранных белков. Сравнение с океаном появилось из-за того, что агрегатное состояние липидов в мембране жидкое, а точнее — жидкокристаллическое. Мембрана сравнительно свободно «течет» в плоскости, в то время как вне нее — строго упорядочена геометрией двойного молекулярного слоя.
«Последней классической» эта теория здесь названа потому, что, с одной стороны, она явно устарела, а с другой — современные представления не достигли еще той лаконичной изящности, чтобы их начала запросто можно было изложить в школьном учебнике [4].
В настоящее время стало понятно, что липидный компонент мембраны — это не просто пассивный носитель белков, которые и выполняют всю работу, но равноправный участник большинства биохимических процессов. На поверку оказывается, что липидный состав мембраны (а она состоит отнюдь не из одного типа молекул липидов!) тщательно оптимизирован эволюцией и позволяет создать необходимые условия для корректной и эффективной работы мембранных белков. Например, частичное взаимное несмешивание липидных компонентов мембраны эукариотической клетки приводит к появлению микроскопических (строго говоря, даже наноскопических) неоднородностей, называемых также мембранными рафтами (от англ. raft — «плот»). Такое сложное фазовое поведение липидного матрикса мембраны активно используется клеткой: упомянутые рафты, предположительно, образуют функциональные платформы, в которых комплексы мембранных белков выполняют все разнообразие своих функций, причем определенные белки предпочитают находиться в рафтовых областях, тогда как другие — в областях между ними.
В данной статье мы постарались осветить современные представления о биофизике липидных компонентов биологических мембран, и в первую очередь, подробнее остановиться на способности липидов к самоорганизации, которая широко используется клетками в своих нуждах.
Рисунок 1. Разнообразие липидов — компонентов клеточных мембран. «Комбинаторное» построение большинства липидов (то есть, сочетание разных гидрофобных, гидрофильных и «адапторных» фрагментов) приводит к тому, что в клетке обнаруживается до 1000 разновидностей липидных молекул. Подавляющее большинство из них играет регуляторную роль, либо их роль не изучена. На рисунке показаны только некоторые основные типы липидов, встречающихся в биологических мембранах.
- Фосфолипиды — один из основных компонентов плазматической мембраны эукариот и бактерий. Являются сложными эфирами жирных кислот («хвосты») и многоатомных спиртов (преимущественно глицерола, сфингозина и инозитола), соединенных через остаток фосфорной кислоты с добавочной группой («головкой»). Глицерофосфолипидов в мембранах по массе больше всего, и это наиболее пластичный и текучий их компонент. В зависимости от типа головки эти липиды делят на классы: фосфатидилхолины (головка — холин), фосфатидилглицеролы, фосфатидилэтаноламины и т.д. Полное название липида включает также наименование жирных кислот, образующих хвосты, например олеиновая (одна двойная связь — C18:1 [9]) и пальмитиновая (все связи насыщены — С16:0) кислоты образуют пальмитоилолеилфосфатидилхолин (ПОФХ), а две молекулы пальмитиновой кислоты — дипальмитоил фосфатидилхолин (ДПФХ).
Сфингофосфолипиды также имеют два ацильных хвоста, но только один из них принадлежит жирной кислоте: второй относится к сфингозину. Один из таких липидов — сфингомиелин (в обилии встречается в миелиновой оболочке аксонов) — является важным компонентом клеточной мембраны, придавая ей жесткость и уникальные физико-химические свойства. Самые простые сфингофосфолипиды называются церамидами. - Холестерол (он же холестерин) — другой важный липид клеточной мембраны, стабилизирующий ее текучесть, — является отличительной чертой мембран эукариот (его нет ни у бактерий, ни у архей). Кроме стабилизации мембран (обычно «в паре» со сфингомиелином), холестерол является предшественником половых гормонов и витамина D. О свойствах холестерола и сфингомиелина подробнее рассказано дальше.
- Гликолипиды, имеющие в качестве полярной головки один или несколько остатков сахаров, также являются компонентами мембран (преимущественно внешнего монослоя). Основной их формой являются гликосфинголипиды, благодаря чему эти липиды, как правило, колокализованы со сфинголипидами (а именно, расположены в жидкой упорядоченной фазе). Основная их роль — межклеточное распознавание, и кроме пользы (например, определения групп крови) эта их функция может быть и вредна: многие ганглиозиды (например, GM1) являются рецепторами бактериальных токсинов и вирусов.
- Липиды мембран архебактерий существенно отличаются от таковых у бактерий и эукариот, — видимо, вследствие эволюционной адаптации к термофильности, галофильности, ацидофильности и прочей экстремофильности, которой знамениты археи. Отличий от фосфолипидов несколько:
- Используется другой стереоизомер глицерола.
- Жирными хвостами служат изопреноидные спирты, а не жирные кислоты.
- Соединяются они с помощью простой, а не сложной эфирной связи.
- Липиды могут быть биполярными (сшиваются концами хвостов), пронизывая при этом всю мембрану насквозь.
- Вместо двойных связей липидные хвосты могут содержать циклопентановые кольца, играющие ту же роль.
Любопытно, что, хотя археи считаются более близкими родственниками эукариот, чем бактерии, такая важная и консервативная черта, как строение мембраны, у них столь сильно отличается от двух других доменов жизни [10], [11].
Многообразие биомембран
Не удивительно, что мембраны клеток разных организмов отличаются между собой. Подробное сравнение липидной составляющей различных мембран наводит на мысль, что эти различия носят принципиальный характер, и что «липидный портрет» той или иной мембраны во многом определяет ее функции (помимо «населяющих» эту мембрану белков) [5]. Так, мембраны бактерий отличаются от мембран эукариот тем, что в состав первых входит большое количество отрицательно заряженных фосфолипидов (например, фосфатидилглицеролы), тогда как вторые в основном содержат липиды цвиттерионной природы (то есть, обладая как отрицательным, так и положительным зарядом, в целом они электронейтральны), — например, фосфатидилхолины. Это фундаментальное отличие используется системой врожденного иммунитета многих эукариот, — например, антимикробные пептиды селективно разрушают мембраны бактерий именно благодаря наличию отрицательного заряда на их поверхности [6], [7], а Toll-подобные рецепторы распознают бактериальные патогены благодаря компонентам их клеточной стенки (липиополисахаридам) [8], [9]. (Химическая структура упоминаемых липидов приведена на рис. 1.)
Другая важная особенность эукариот — холестерол (известный также как холестерин), отсутствующий в прокариотических мембранах. Вопреки своей дурной славе у обывателей [12], холестерол играет важнейшую и еще, видимо, не до конца осознанную роль в работе мембран наших клеток (не говоря уже о том, что он является предшественником половых гормонов). Вместе со сфинголипидами (такими как сфингомиелин) холестерол образует рафтовые структуры, придающую эукариотическим мембранам прочность и особую функциональную гетерогенность, о чем подробнее будет сказано ниже.
Интересно, что липидный состав разных органелл существенно отличается (рис. 2). Например, липидный состав митохондрий и пластид гораздо больше напоминает бактериальный, нежели эукариотический, подтверждая тем самым химерную гипотезу становления эукариот (эукариогенеза), согласно которой эти органеллы — бывшие бактерии, захваченные во «внутриклеточный плен» путем фагоцитоза какими-то ранними формами эукариот [13]. В эндоплазматическом ретикулуме, являющемся «стартовой точкой» метаболизма большинства липидов, состав обоих листков мембраны примерно одинаковый, однако в аппарате Гольджи, плазматической мембране и эндосомах различия уже весьма существенны, что говорит о наличии активных процессов, создающих эту асимметрию. В частности, фосфатидилсерины (ФС) и фосфатидилэтаноламины (ФЭ) в норме присутствуют только в цитоплазматическом листке плазматической мембраны. Наличие ФС на поверхности клетки может говорить о злокачественном перерождении и запускает программы фагоцитоза и сворачивания крови.
Рисунок 2. Липидный состав различных мембранных структур клеток млекопитающих. Диаграммы показывают липидный состав некоторых клеточных мембран; содержание холестерола (ХОЛ) дано в отношении к суммарному количеству фосфолипидов (ФЛ). Внутри клетки обозначены места синтеза основных фосфолипидов (голубые овалы) и сигнальных липидов (красные овалы) (последних по массе не более 1% от фосфолипидов, за исключением церамидов (Цер)). В эндоплазматическом ретикулуме (ЭПР) синтезируются в основном глицерофосфолипиды, жиры, холестерол и церамиды. Аппарат Гольджи является «поставщиком» сфингомиелина и сложных гликосфинголипидов. Около половины липидов митохондрий (в основном, фосфатидилэтаноламина (ФЭ), фосфатидной кислоты (ФК) и кардиолипина (КЛ)) синтезируется этими органеллами автономно, что, вместе с типично «бактериальным» липидным составом их мембран, говорит в пользу химерной теории эукариогенеза.
Условные обозначения: БМФ — бисмоноацилглицерофосфат; ГалЦер — галактозилцерамид; ГСЛ — гликосфинголипиды; ДАГ — диацилглицерол; КЛ — кардиолипин; СМ — сфингомиелин; ТГ — триацилглицеролы (жиры); ФГ — фосфатидилглицерол; ФИ — фосфатидилинозитол; ФК — фосфатидная кислота; ФС — фосфатидилсерин; ФХ — фосфатидилхолин; ФЭ — фосфатидилэтаноламин; Хол — холестерол; Цер — церамид; PI(?)P — фосфатидилинозитолфосфаты; S1P — сфингозин-1-фосфат; Ост. — остальные липиды.
Совершенно уникальной организацией мембран обладают архебактерии — третий «домен» жизни [10], [11], наряду с бактериями и эукариотами. Эволюционно они считаются более близкими родственниками эукариот, нежели бактерий, хотя по строению липидов мембраны этого не скажешь [14]. Видимо, как адаптация к экстремофильности (способности обитать при высокой температуре и/или солености и/или кислотности), мембраны архей содержат липиды с нетипичным химическим строением (см. рис. 1):
- используется другая конфигурация остатка глицерола;
- неполярные «хвосты» крепятся к этому остатку не сложными, а простыми эфирными связями;
- хвосты имеют не линейную структуру, а состоят из изопреновых звеньев, и, что самое интересное, архейные липиды могут быть биполярными («сшитыми» кончиками и пронизывающими всю мембрану насквозь) и содержать для большей прочности циклопентановые кольца, предположительно выполняющие функцию двойных связей в «обычных» фосфолипидах (регулирование температуры плавления).
Из всего сказанного следует, что липидный состав мембран отнюдь не является чем-то выбранным раз и навсегда [15]: он претерпел существенные изменения в процессе эволюции. Даже в разные периоды жизни одного и того же организма состав мембран может существенно варьировать. По всей видимости, липидную организацию мембран эукариот можно считать эволюционно наиболее прогрессивной, поскольку она обеспечивает максимально гибкую адаптацию микроскопического окружения под нужды белковых молекул, создавая частично изолированные области в пределах одной, казалось бы, жидкой фазы. Далее мы остановимся на этих аспектах функционирования гетерогенной эукариотической мембраны подробнее.
Латеральная гетерогенность эукариотических мембран
Что же заставило исследователей обратить внимание на то, что мембрана — это нечто более сложно устроенное, нежели липидный «океан», в котором плавают «айсберги» белков, согласно модели Сингера-Николсона? Можно сформулировать три основных аргумента, почему клеточная мембрана должна быть устроена более сложно и организованно, чем это было принято считать в те годы:
- В каждой эукариотической клетке присутствует более 1000 разновидностей липидов — такое разнообразие обеспечивается возможностью комбинации различных полярных «головок» и гидрофобных «хвостов» [5], [16]. Из этого следует многообразие ролей липидов в организме, — хотя структурные свойства мембран определяются, видимо, основными тремя–четырьмя компонентами (если не считать белков, конечно).
- Распределение липидов и белков в плоскости мембраны неоднородно, а, напротив, обладает характерной структурой, — это принято называть латеральной гетерогенностью. Гетерогенная организация наблюдается и для сравнительно простых (например, трехкомпонентных) смесей липидов, используемых в качестве моделей биомембран: в пределах единой жидкокристаллической фазы появляются микрофазы, не смешивающиеся между собой (см. далее). В мембранах клеток подобная самоорганизация обеспечивает сортировку мембранных белков в различные компартменты в пределах одной и той же поверхности, повышая эффективность взаимодействия белков между собой.
- Функциональное состояние мембраны существенно неравновесно. Оно может быть стационарным (когда концентрации разных липидов сохраняются примерно на том же уровне), но обязательно включает непрерывный обмен веществом (регенерация и «отпочковывание» участков мембраны). Таким образом, неравновесные диссипативные процессы играют важную роль не только в биохимии, но даже и в биофизике мембраны.
В практическом смысле вышеперечисленное обозначает, что липидная компонента, будучи жидкой, тем не менее, способна образовывать частично изолированные области бислоя, обладающие особыми структурными свойствами. Эти участки представляют собой кластеры («островки») молекул липидов, сравнительно более упорядоченные и «твердые», чем окружающая их более «жидкая» фаза. В конце 1990-х такие кластеры получили уже упомянутое название рафтов [17], и то же самое название было дано новой теории организации биологических мембран.
Сосуществование двух жидких липидных фаз — относительно более и менее упорядоченной — оказывается возможным, если липидная смесь содержит как минимум три компоненты: «легкоплавкий» липид (низкая температура плавления, ненасыщенные хвосты), «тугоплавкий» липид (температура плавления выше физиологической, насыщенные хвосты и/или высокая склонность образовывать водородные связи с соседями), а также холестерол. «Тугоплавких» липидов в эукариотической мембране немного, потому что иначе она была бы гелеобразной массой вроде маргарина: основным является сфингомиелин (производное церамида, рис. 1).
Рисунок 3. «Жидкое упорядоченное» состояние липидов в модельных мембранах. а — Фазовая диаграмма тройной смеси холестерола (Хол), сфингомиелина (СМ) и пальмитоилолеилфосфатидилхолина (ПОФХ) (при 23 °C). Цветные области соответствуют составам, при которых мембрана пребывает в жидком состоянии. Сосуществование жидкой упорядоченной (Lo) и жидкой неупорядоченной (Ld) фаз показано синим цветом: здесь при увеличении концентрации холестерола в диапазоне 10–35% размеры доменов «жидкой упорядоченной» фазы постепенно увеличиваются. б — Образование макроскопических мембранных доменов в гигантских везикулах, состоящих из насыщенного (ДПФХ) и ненасыщенного (ДОФХ) фосфолипидов, а также холестерола. Домены окрашиваются флуоресцентными красителями, «предпочитающими» упорядоченную (Lo) или неупорядоченную (Ld) фазы. При увеличении концентрации холестерола сверх 16% макроскопических доменов уже не заметно, но разделение Lo/Ld продолжает существовать, о чем говорит низкий сигнал резонансного переноса энергии между молекулами красителя разных типов, находящихся в разных доменах (примерное положение двух верхних микрофотографий везикул обозначено справа желтым кругом).
Такая тройная смесь «туго-» и «легкоплавкого» липидов с холестеролом демонстрирует сложное фазовое поведение (рис. 3). По всей видимости, молекулы холестерола играют роль «центров кристаллизации» для доменов из «тугоплавких» липидов, однако его присутствие в то же время не позволяет им образовать твердую (гелевую) фазу. Чтобы точнее понять возможные фазовые состояния в мембране и сложных липидных смесях, ее изображающих, введем следующие обозначения:
- Твердая фаза (гель) — So (от solid ordered). Характерна высоко упорядоченным состоянием липидных «хвостов», приблизительно параллельных друг другу. Толщина бислоя, состоящего из липидов в этом состоянии, будет максимальной, а площадь, приходящаяся на молекулу, — минимальной. Проще всего гелевую фазу себе представить, вспомнив маргарин.
- Жидкая (жидкокристаллическая) фаза — L (от liquid). В биологических мембранах и сложных смесях существует две разные (и взаимно несмешивающиеся) жидкие фазы:
- Жидкая упорядоченная фаза — Lo (от liquid ordered). Эту фазу можно считать синонимом рафтов и липидных доменов в мембране. Отличается достаточно высокой упорядоченностью липидных «хвостов» (что напрямую подтверждается такими экспериментальными методиками, как рентгеновская дифракция, рассеяние нейтронов или спектроскопия ядерного магнитного резонанса), а значит, и большей толщиной состоящих из нее липидных доменов (и меньшей площадью, приходящейся на одну молекулу липида). При всем при том, Lo-фаза обладает высокой латеральной подвижностью (за счет малого размера рафтов в мембране), что помещает ее примерно посередине между жидкостью и твердой фазой (так называемая «мезофаза»).
- Жидкая неупорядоченная фаза — Ld (от liquid disordered). Это настоящая, свободно перемешивающаяся, жидкость, — только в двух измерениях (поскольку в бислое третье измерение фактически отсутствует). Липидные «хвосты» в этой фазе максимально неупорядочены, и площадь на одну молекулу липида в связи с этим максимальна. Проще всего жидкую фазу Ld себе представить, посмотрев на масляное пятно, на поверхности которого переливаются радужные узоры.
Равновесие между Lo/Ld фазами было давно показано на искусственных мембраноподобных системах (например, гигантских везикулах, изготовленных из липидов легочного сурфактанта) (рис. 3б), однако непосредственно в биологической мембране такого разделения (а, значит, и рафтов) пронаблюдать долгое время не удавалось. В чем же дело, если липидный состав искусственных мембран был подобран максимально похожим на мембраны настоящие?
Проблема заключается в том, что в биологических мембранах жидкая упорядоченная фаза сильно «раздроблена», и максимальный размер рафтов не превышает 100 нм, что недоступно для непосредственного наблюдения в оптический микроскоп. (Даже флуоресцентная конфокальная микроскопия, делающая «видимыми» отдельные светящиеся молекулы, в данном случае не сможет сказать, находятся ли определенные белки и пептиды в пределах одного кластера или нет.) Причины, в силу которых в живой клетке рафты не сливаются в крупные домены, видимые в оптический микроскоп (а именно это и происходит в искусственных мембранах), мы обсудим чуть дальше.
Рисунок 4. Рафтовые неоднородности в мембране различного масштаба. а — Нанокластеры холестерола, сфингомиелина, гликосфинголипидов и белков плазматической мембраны различаются по составу. Считается, что в эти кластеры входят ГФИ-заякоренные белки, трансмембранные (ТМ) белки, специфичные для рафтов, и цитоплазматические белки, связанные с актиновыми филаментами. «Обычные» ТМ-белки не входят в состав рафтов. б — В ответ на внешние сигналы нанокластеры могут сливаться с образованием рафтовой платформы, важной для ТМ передачи сигналов и мембранного транспорта. в — Рафтовая фаза, видимая в микроскоп (ø ≈1 мкм), наблюдается исключительно в равновесных мембранных системах, таких как гигантские синтетические или мембранные везикулы. В «нативных» мембранах постоянный обмен веществом и энергией «дробит» рафтовую фазу до субдифракционных размеров.
На маленьком липидном плоту
Гипотеза рафтов восходит к наблюдению, что гликосфинголипиды в комплексе Гольджи распределены не равномерно, а кластеризуются вместе перед тем, как направляться к полюсам поляризованных эпителиальных клеток. Лабораторное изучение этих кластеров показало, что, в отличие от «обычных» участков мембран, эти кластеры не растворяются в детергенте тритон X-100: они более прочные и устойчивые. Согласно химическому анализу, эти кластеры состоят преимущественно из холестерола и сфингомиелина (рис. 1), а основные белки, неизменно попадающие в эти кластеры — это гликозилфосфатидилинозитол (ГФИ)-заякоренные белки (GPI-anchored proteins). Было сделано предположение, что эти плотные кластеры образуют стабильные «плоты» (размером примерно 50 нм), в которые встроены определенные типы белков. Дополнительно в пользу этой концепции говорил тот факт, что синтетические мембраны, содержащие холестерол и гликосфинголипиды, демонстрируют примерно те же свойства: липиды разделяются на две несмешивающиеся фазы, которые даже можно разглядеть в микроскоп (рис. 3б).
Однако с течением времени стало понятно, что такое представление — противоположная крайность по сравнению с жидкостно-мозаичной моделью Сингера и Николсона: рафты далеко не столь стабильны, как это было постулировано первоначально. По всей видимости, это динамические структуры, постоянно обменивающиеся молекулами липидов и белков с остальной частью мембраны. При этом липиды в рафтах упакованы гораздо более плотно и структурированно, нежели в окружающей «жидкой» мембране. Сравнительно современное определение рафтов звучит так:
Однако, несмотря на то, что определение рафтам дано, само их существование представлялось до недавнего времени довольно-таки спорным, то есть — не подтвержденным в прямом эксперименте. Как же понимать этот парадокс?
Дело в том, что существование мембранной фракции, не растворимой в детергентах — это еще не повод считать эту фракцию рафтами (функциональными неоднородностями). Непосредственное же изучение этих доменов затруднено в связи с тем, что рафты очень сложно наблюдать «напрямую» из-за их малого размера: типичный их предполагаемый диаметр меньше дифракционного предела оптической микроскопии (≈200 нм). (Здесь речь идет именно об оптическом, а не рентгеновском или электронном излучении, потому что только оно позволяет наблюдать за клеткой неинвазивно, то есть — не разрушая ее.) Правда, в последние годы уже появились экспериментальные методики непосредственного наблюдения рафтовых кластеров (см. таблицу). В частности, одна из разновидностей оптической микроскопии сверхвысокого разрешения — наноскопия индуцировано-истощенного излучения (stimulated emission depletion, STED) — позволила установить, что ГФИ-заякоренные белки в течение достаточно длительного времени (10–20 мс) захватываются в сфинголипидно-холестерольные домены размером <20 нм в мембранах живых клеток, — то есть, в рафты [21]. (Кстати, ГФИ-заякоренные белки — один из основных компонентов рафтов в биомембранах, и попадают они туда самопроизвольно. Подробнее об этом будет рассказано далее.)
Но даже с помощью этих точнейших наблюдений невозможно проникнуть в детали межмолекулярных взаимодействий, заставляющих липиды собираться в кластеры, а также «захватывать» с собой белки. С другой стороны, подобная информация может быть получена с привлечением методов компьютерного моделирования.
Рисунок 5. Микроскопия подавления индуцированного излучения (STED) — инновационный способ неинвазивного наблюдения липидной динамики мембран в наномасштабе. STED-микроскопия — один из ультрасовременных оптических методов сверхвысокого разрешения, позволяющих «заглянуть за» дифракционный барьер (то есть, различать объекты, меньшие ≈200 нм). Образование «упорядоченной жидкой» фазы (Lo) связано с образованием доменов, обогащенных холестеролом и сфингомиелином, что можно установить при помощи метода флуоресцентно-резонансного переноса энергии (FRET). Однако размер зоны, в пределах которой «обычный» конфокальный микроскоп (слева) позволяет различать детали (≈250 нм), оказывается слишком велик, чтобы точно определить, движутся ли две молекулы совместно (то есть, образуют домен) или независимо. STED-микроскопия с размером «зоны наблюдения» всего 50 нм (справа) позволила установить существование холестерольно-сфингомиелиновых доменов на живых клетках, положив конец спору о существовании рафтов в живых клетках.
Внизу. Принцип STED-методики сходен с конфокальной флуоресцентной микроскопией, но здесь, кроме возбуждающего лазерного импульса (слева), запускающего свечение молекул-флуорофоров, используется также кольцевой формы гасящий импульс (в центре), уменьшающий эффективный радиус зоны возбуждения флуорофоров до ≈50 нм (справа; это в 4–5 раз меньше пресловутого «дифракционного барьера»).
| Метод | Что наблюдает | Пространственное / временное разрешение | Пояснение |
|---|---|---|---|
| Спектроскопия скоррелированной флуоресценции (FCS) | Подвижность флуорофора и латеральная гетерогенность | ~250 нм / ~1 мкс | Чувствителен к кластеризации; использование нескольких цветов |
| Флуоресцентно-резонансный перенос энергии (FRET) | Сближенность донора и акцептора | ~5–10 нм (расстояние между флуорофорами) / <1 с | Идентификация кластеров в нанометровом диапазоне |
| Отслеживание одиночных частиц (SPT) | Траектории наночастиц (золото, квантовые точки) | ~ 250 (10а) нм / <25 мкс | Чувствительность для одиночных молекул, идентификация кластеров |
| Флуоресцентная микроскопия одиночных молекул (SMFI) | Флуоресценция отдельных молекул | ~ 250 (20а) нм / <30 мс | Различает, входят ли в обесцвеченный лазером участок одиночные молекулы или димеры |
| Картирование тепловых движений (TNI) | Частица, прикрепленная к компоненту мембраны, «захватывается» лазером | ~10 нм / ~1 мкс | Исследуется движение частицы, «захваченной» лучом лазера |
| Микроскопия подавления индуцированного излучения (STED) | Флуоресцентный или FRET-сигнал | ~50 нм / 1 мс | «Область обзора» эффективно сужается за счет гасящего импульса |
| a — Точность в определении центра изображения |
Кластеризация липидов in silico
Современные методы молекулярного моделирования позволяют изучить процесс самоорганизации липидных смесей с разной степенью детализации. Расчеты молекулярной динамики (МД; [7], [22]) модельных мембран, в которых все атомы липидов и окружающего растворителя представлены в явном виде, дают наиболее полную информацию. И хотя при таком подробном рассмотрении системы, доступные для моделирования даже на современных суперкомпьютерах, ограниченны в своих размерах (102–103 молекул липида) и длительности наблюдения за их динамическим поведением (<10−6 c), получаемые результаты дают атомарную картину возникновения мембранных неоднородностей в наномаштабе. Даже в случае однокомпонентной липидной мембраны ее поверхность не является однородно полярной, как это можно предположить из схематического представления липидов в виде «шариков с хвостиками» — часть этих «хвостиков» всплывает на границу вода—мембрана и формирует гидрофобные участки (рис. 6). В итоге мы имеем мозаично организованную поверхность, на которой в полярном «море» рассредоточены гидрофобные «островки» размером до нескольких нм2 [23].
Рисунок 6. Мозаичная организация поверхности простейшей однокомпонентной мембраны. Слева представлена идеальная модель мембраны, справа — поверхность полноатомной мембраны (ДОФС), раскрашенной по гидрофобности.
Рисунок 7. Предпочтительная локализация трансмембранных пептидов WALP23 в Ld-фазе. Модельная мембрана состоит из липидов ДЛФХ, ДПФХ и холестерола.
При смешивании двух компонентов, например насыщенного (дипальмитоил-) и ненасыщенного (диолеил-) фосфатидилхолинов (ДПФХ и ДОФХ, соответственно), картина усложняется, и наблюдается обособление более «твердой» фазы (ДПФХ) в стабильные нанокластеры, распределенные диффузно в плоскости мембраны [24]. При моделировании трехкомпонентных мембран, в состав которых входят холестерол, сфингомелиеин и ДОФХ даже на небольших временах МД (2×10−7 с) наблюдается настоящее фазовое разделение, при котором «тугоплавкий» сфингомелеин формирует островок, по границе которого располагается холестерол, обращенный своей «щетинистой» стороной во внешнюю фазу «легкоплавкого» ДОФХ [25].
Увеличить время наблюдения за поведением многокомпонентных мембран in silico, а также размер моделей, позволяет упрощенное («крупнозернистое») описание молекул. Атомы объединяют в обособленные группы — «зерна» (обычно 3–4 атома), — для которых производят расчет МД. Такая методика позволила впервые «увидеть» разделение Lo/Ld фаз в мембране из нескольких тысяч молекул, содержащей 40% насыщенного ДПФХ, 30% ненасыщенного дилинолеилфосфатидилхолина (ДЛФХ) и 30% холестерола, моделируемых в течение 20 мкс [26]. Более того, если к такой модельной мембране добавить трансмембранные спиральные пептиды (минимальные «строительные блоки» большинства мембранных белков), то можно наблюдать, как происходит их сортировка между фазами — моделируемые фрагменты белка предпочитают находиться в более жидкой Ld-фазе (ДЛФХ) и избегают упорядоченной Lo-фазы ДПФХ (рис. 7) [27].
Стоит отметить, что возникновение латеральной гетерогенной структуры в мембране наблюдается не только при смешивании «тугоплавких» и «легкоплавких» липидов, но также любых других отличающихся по своим физико-химическим свойствам — например, заряду полярной головки и склонности образовывать водородные связи с соседями. В частности, в модельной бактериальной мембране, содержащей 70% фосфатидилэтаноламина (ФЭ) и 30% отрицательно зараженного фосфатидилглицерола (ФГ) также наблюдается формирование нанодоменов, — за счет того, что молекулы ФЭ эффективно взаимодействуют друг с другом и вытесняют «невыгодного» партнера ФГ. На «крупнозернистых» моделях была показано, что такая латеральная организация мембран бактерий используется в процессе связывания антимикробными пептидами, которые при этом вызывают рост доменов ФГ и возникновение фазового разделения [28].
Что ограничивает размер рафтов в биомембранах
В реальных экспериментальных системах наблюдается достаточно парадоксальный контраст с искусственными мембранами, разделение фаз Lo/Ld в которых наблюдали неоднократно и при разных условиях. В живой клетке это удалось сделать непосредственно лишь недавно, да и то — используя самые современные технологии субдифракционного наблюдения [21]. В чем же причина такого разительного отличия?
Ведь на границе рафтовой фазы создается поверхностное (линейное) натяжение, а значит, присутствует избыточная свободная энергия, снизить которую можно путем слияния отдельных «плотиков» в одну большую макрофазу. Примерно то же самое наблюдается в супе, мелкие капли жира на поверхности которого постепенно объединяются в более крупные пятна. Фактически, это самое и происходит в искусственных мембранах (например, в мембранных везикулах) — самопроизвольный термодинамический процесс толкает к глобальному разделению Lo и Ld фазы. Но это обозначает, что отсутствие в живой клетке крупных Lo-кластеров — следствие активных процессов, протекающих с затратой энергии. (Возвращаясь к аналогии с супом, мы никогда не увидим одного большого пятна жира в кипящей кастрюле.) С одной стороны, это может происходить «само», поскольку мембрана, как и сама жизнь, — система, далекая от термодинамического равновесия. С другой стороны, эволюция физико-химических свойств мембраны могла направленно выработать такое приспособление, поскольку оно позволяет мембранам выполнять свои функции более эффективно.
Так или иначе, в мембранах протекает ряд процессов, постоянно «дробящих» рафты, — именно поэтому их так долго и не могли с достаточной степенью уверенности «нащупать». Это постоянный обмен веществом и энергией — ведь мембраны представляют собой открытые системы: помимо многочисленных разновидностей везикулярного транспорта, отдельные фрагменты мембраны постоянно «заглатываются» внутрь клетки и после какой-то переработки возвращаются обратно. Кроме этого, специальные белки делят мембрану, подобно «заборчикам», на отдельные участки. С одной стороны, это способствует компартментализации, с другой — также препятствует росту рафтов.
Анализ огромного массива биохимических и биофизических данных относительно липидных доменов в биомембранах, накопившихся за последние 15 лет, привел ученых к выводу, что состав липидного матрикса мембран эволюционно подобран, чтобы при физиологических условиях всегда находиться вблизи фазового перехода (рис. 8). Это способствует образованию в мембранах мезофазы (рафтов), которые, несмотря на свой малый размер и динамическую природу, играют важную (хотя не до конца еще изученную) роль. Какую? Читайте в заключительной части статьи.
Рисунок 8. Динамическая модель рафтов. Домены «жидкой упорядоченной» фазы (Lo) в мембране гетерогенны как по размеру, так и по времени существования (0,1 мс — 1 с, показано цветом): это зависит от размера, липидного состава и «захваченных» белков, способных стабилизировать рафт. (Длина пунктирных стрелок, изображающих латеральную подвижность доменов, пропорциональна времени жизни.) Маленькие Lo-домены формируются спонтанно и диффундируют в плоскости мембраны (a). Захватив ГФИ-заякоренный или другой рафтовый белок (b), такой домен становится стабильнее и образует комплекс (c), способный или просто распасться (d), или, слившись с другим, увеличить размер (e). Такие столкновения могут привести к формированию более крупного и стабильного Lo-белкового комплекса (f), либо через какое-то время распадающегося самостоятельно, либо захватываемого в эндоцитозный пузырек (h) и «разбираемого» на исходные составляющие (i). Таким образом, рафтовые платформы в биомембранах, хотя и выполняют важные функции, являются динамическими структурами, постоянно возникающими и пропадающими вновь.
Биологическая роль наноразмерных неоднородностей в мембране
Роль такого сложного фазового поведения липидного матрикса мембран еще только предстоит понять в полной мере. Впрочем, сегодня ясно главное — такие свойства позволяют группировать (сортировать) разные белки в частично изолированные области, что позволяет им выполнять предназначенные функции. Также эти свойства определяют то, каким образом мембраны делятся и сливаются, — а это и деление самих клеток, и везикулярный транспорт, и жизненный цикл вирусов, и способность многих токсинов проникать внутрь клеток. Рассмотрим несколько примеров биологической роли рафтов немного более подробно [20]:
- Передача сигналов при дифференциации Т-лимфоцитов. В основе приобретенного иммунитета лежит процесс «обучения» Т-лимфоцитов распознавать определенные антигены и уничтожать их. Это происходит при непосредственном контакте антиген-презентирующей клетки (АПК) с «наивным» лимфоцитом, который, «обучившись», многократно делится и дает начало целой колонии идентичных Т-лимфоцитов, способных распознавать именно этот антиген.
Что интересно, рецепторы Т-клеток, которые распознают «заряженный» антигеном главный комплекс гистосовместимости на поверхности АПК, кластеризуются именно в рафтовой фазе, и дополнительно скрепляются актиновыми нитями со стороны цитоплазмы. Это скопление рецепторов обеих клеток формирует иммунологический синапс (область плотного контакта) между Т-лимфоцитом и АПК.
В лабораторных экспериментах подтверждено, что участие рафтовой фазы в формировании иммунологического синапса принципиально: изъятие из мембран холестерола или модификация некоторых участвующих в процессе белков, чтобы они теряли сродство к рафтам, приводит к тому, что презентирования антигена не происходит, и иммунитет не образуется. - «Почкование» вирусных частиц. Многие вирусы, покидая зараженную ранее клетку, облачаются в липидную оболочку — часть мембраны клетки-хозяина. Некоторые из них, в частности ВИЧ и вирус гриппа, «отпочковываются» от рафтовых участков мембраны, что приводит к тому, что вокруг их собственного нуклеокапсида образуется липидная «скорлупа», состоящая целиком из рафтовых липидов. Делается это, видимо, затем, чтобы в оболочку попали вирусные гликопротеины и не попадали ненужные вирусу мембранные белки клетки-хозяина.
Опять же, эксперименты показывают, что «почкование» — процесс, зависящий от наличия холестерола и сфинголипидов, что подтверждает участие рафтовой фазы. - Участие рафтов в мембранном транспорте. Секреция секретируемых и доставка мембранных белков начинаются с эндоплазматического ретикулума (ЭР) с «промежуточной остановкой» в комплексе Гольджи. В этом транспорте на основе все тех же принципов разделения фаз в липидных системах играет роль жидкая упорядоченная фаза (рафты). На примере ЭР дрожжей установлено, что существует три различных сайта выхода везикул с белковым «грузом» из ЭР: два из них отвечают за транспорт растворимых секретируемых и мембранных белков, а третий является «портом отправления» ГФИ-заякоренных белков, в мембране клетки расположенных внутри рафтов. Так вот уже на стадии ЭР эти белки транспортируются в везикулах, по составу близких к рафтам (насыщенных холестеролом и церамидами).
Аналогичная ситуация наблюдается и с комплексом Гольджи, откуда к мембране идут везикулы, либо покрытые клатриноподобной белковой оболочкой, либо состоящие из рафтовых липидов. Кстати, сама гипотеза рафтов была выдвинута в связи с наблюдением процесса сортировки белков и липидов в комплексе Гольджи: оказалось, что к апикальным поверхностям эпителиальных клеток отправляются пузырьки, несущие строго определенные белки.
Дополнительно подтверждая роль жидкой упорядоченной фазы в мембранном транспорте, было установлено, что некоторые ферменты, участвующие в синтезе холестерола и сфинголипидов, необходимы для доставки рафтовых белков в мембрану клетки. - Некоторые рафтовые липиды — «троянские кони» для бактериальных токсинов и вирусов. В частности, шигатоксин (токсин бактерий, вызывающих дизентерию [30]) и холерный токсин, формируя пентамерный «бублик», захватывают рафтовые гликосфинголипиды под названием ганглиозиды Gb3 и GM1, что провоцирует образование «впячиваний» мембраны в виде трубочек, что лежит в основе токсического действия этих микроорганизмов. Аналогичным образом в клетку проникает вирус SV40: он связывается с ганглиозидом GM1 и кластеризует его; это приводит к образованию мембранного «впячивания» и захвата вируса в эндосому, направляющуюся в сторону ЭР.
«Троянская» роль ганглиозидов подтверждается отсутствием токсичности и способности вируса проникать внутрь клетки при действии на синтетические аналоги этих ганглиозидов, имеющие более короткий жирный «хвост» и сортирующиеся не в рафтовую, а в жидкую неупорядоченную фазу (Ld, или, проще говоря, «обычную» мембрану).
Интересно, что у бактерий тоже есть липид мембраны (называемый липидом-II), действующий в роли троянского коня для некоторых антибиотиков, однако этот липид не имеет отношения к рафтам, а является предшественником клеточной стенки, без которой бактерии погибают.
Перспективы биофизического изучения мембран
Кажущаяся простота липидного «океана» осталась в прошлом, и сейчас исследователи лишь приблизительно представляют все молекулярные тонкости образования кластеров в липидах. Точно так же далек от понимания и механизм «сортировки» одних белков в рафтовую фазу, а других — в более жидкую область мембраны. Между тем, это понимание дало бы возможность создать стратегию рафт-селективной доставки в клетку различных веществ, — в том числе, лекарств.
Все рассказанное в этой статье относится в первую очередь к мембранам эукариот, — но это еще не обозначает, что у бактерий нет ничего подобного (раз нет и холестерола). Изучение латеральной неоднородности бактериальных мембран может привести к созданию новых поколений антибиотиков, избирательно уничтожающих патогенные микроорганизмы, и свободных от проклятия резистентности, давно уже нависшего над «традиционными» антибактериальными средствами.
История с изучением липидного матрикса мембран в очередной раз показывает, что живая материя устроена значительно сложнее, чем представлялось ранее, и изобретение новых высокоточных методик наблюдения лишь усугубляет эту сложность.
Статья написана в соавторстве с Антоном Полянским и при поддержке РФФИ (конкурс на написание научно-популярных статей), № проекта: 11-04-11516-с. В сокращенном виде она опубликована в «Природе» [31].
Литература
- К вопросу о происхождении жизни;
- Антонов В.Ф. (1996). Биофизика мембран. Соросовский образовательный журнал. 6;
- S. J. Singer, G. L. Nicolson. (1972). The Fluid Mosaic Model of the Structure of Cell Membranes. Science. 175, 720-731;
- Luis A. Bagatolli, John H. Ipsen, Adam C. Simonsen, Ole G. Mouritsen. (2010). An outlook on organization of lipids in membranes: Searching for a realistic connection with the organization of biological membranes. Progress in Lipid Research. 49, 378-389;
- Gerrit van Meer, Dennis R. Voelker, Gerald W. Feigenson. (2008). Membrane lipids: where they are and how they behave. Nat Rev Mol Cell Biol. 9, 112-124;
- Антимикробные пептиды — возможная альтернатива традиционным антибиотикам;
- Компьютерные игры в молекулярную биофизику биологических мембран;
- Иммунологическая Нобелевская премия (2011);
- Толл-подобные рецепторы: от революционной идеи Чарльза Джейнуэя до Нобелевской премии 2011 года;
- Эволюция между молотом и наковальней, или Как микробиология спасла эволюцию от поглощения молекулярной биологией;
- Гигантские вирусы: 4-й домен жизни?;
- Наночастицами — по «плохому» холестерину!;
- T. Cavalier-Smith. (2009). Predation and eukaryote cell origins: A coevolutionary perspective. The International Journal of Biochemistry & Cell Biology. 41, 307-322;
- Y.H. Itoh, A. Sugai, I. Uda, T. Itoh. (2001). The evolution of lipids. Advances in Space Research. 28, 719-724;
- Mari Gotoh, Ayae Sugawara, Kazunari Akiyoshi, Isamu Matsumoto, Guy Ourisson, Yoichi Nakatani. (2007). Possible Molecular Evolution of Biomembranes: from Single-Chain to Double-Chain Lipids. C&B. 4, 837-848;
- Daniele Piomelli, Giuseppe Astarita, Rao Rapaka. (2007). A neuroscientist’s guide to lipidomics. Nat Rev Neurosci. 8, 743-754;
- Kai Simons, Elina Ikonen. (1997). Functional rafts in cell membranes. Nature. 387, 569-572;
- John F. Hancock. (2006). Lipid rafts: contentious only from simplistic standpoints. Nat Rev Mol Cell Biol. 7, 456-462;
- Ken Jacobson, Ole G. Mouritsen, Richard G. W. Anderson. (2007). Lipid rafts: at a crossroad between cell biology and physics. Nat Cell Biol. 9, 7-14;
- Kai Simons, Mathias J. Gerl. (2010). Revitalizing membrane rafts: new tools and insights. Nat Rev Mol Cell Biol. 11, 688-699;
- Christian Eggeling, Christian Ringemann, Rebecca Medda, Günter Schwarzmann, Konrad Sandhoff, et. al.. (2009). Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 457, 1159-1162;
- Молекулярная динамика биомолекул. Часть I. История полувековой давности;
- Anton A. Polyansky, Pavel E. Volynsky, Alexander S. Arseniev, Roman G. Efremov. (2009). Adaptation of a Membrane-active Peptide to Heterogeneous Environment. II. The Role of Mosaic Nature of the Membrane Surface. J. Phys. Chem. B. 113, 1120-1126;
- Darya V. Pyrkova, Natalya K. Tarasova, Timothy V. Pyrkov, Nikolay A. Krylov, Roman G. Efremov. (2011). Atomic-scale lateral heterogeneity and dynamics of two-component lipid bilayers composed of saturated and unsaturated phosphatidylcholines. Soft Matter. 7, 2569;
- Sagar A. Pandit, Eric Jakobsson, H.L. Scott. (2004). Simulation of the Early Stages of Nano-Domain Formation in Mixed Bilayers of Sphingomyelin, Cholesterol, and Dioleylphosphatidylcholine. Biophysical Journal. 87, 3312-3322;
- H. J. Risselada, S. J. Marrink. (2008). The molecular face of lipid rafts in model membranes. Proceedings of the National Academy of Sciences. 105, 17367-17372;
- L. V. Schafer, D. H. de Jong, A. Holt, A. J. Rzepiela, A. H. de Vries, et. al.. (2011). Lipid packing drives the segregation of transmembrane helices into disordered lipid domains in model membranes. Proceedings of the National Academy of Sciences. 108, 1343-1348;
- Anton A. Polyansky, Rajesh Ramaswamy, Pavel E. Volynsky, Ivo F. Sbalzarini, Siewert J. Marrink, Roman G. Efremov. (2010). Antimicrobial Peptides Induce Growth of Phosphatidylglycerol Domains in a Model Bacterial Membrane. J. Phys. Chem. Lett.. 1, 3108-3111;
- Jan Domański, Siewert J. Marrink, Lars V. Schäfer. (2012). Transmembrane helices can induce domain formation in crowded model membranes. Biochimica et Biophysica Acta (BBA) — Biomembranes. 1818, 984-994;
- Огурцы-убийцы, или Как встретились Джим Уотсон и Гордон Мур;
- Чугунов А.О., Полянский А.А., Ефремов Р.Г. Липидный фундамент жизни. «Природа». 3, 3–12.