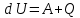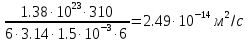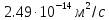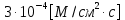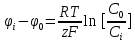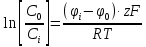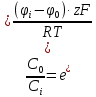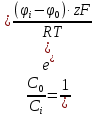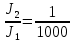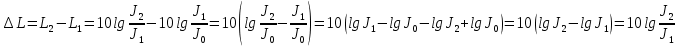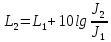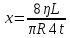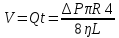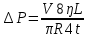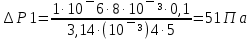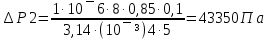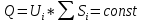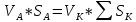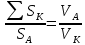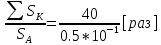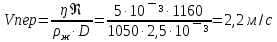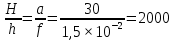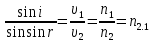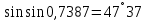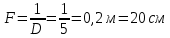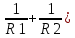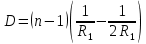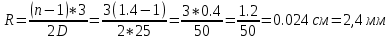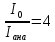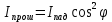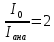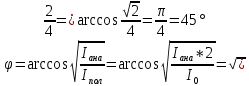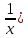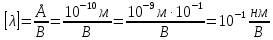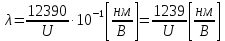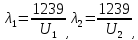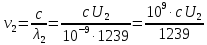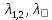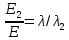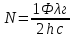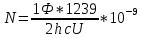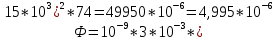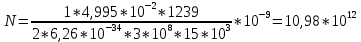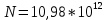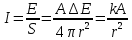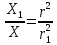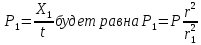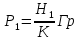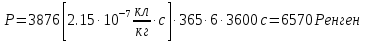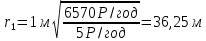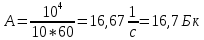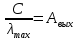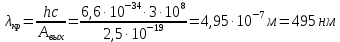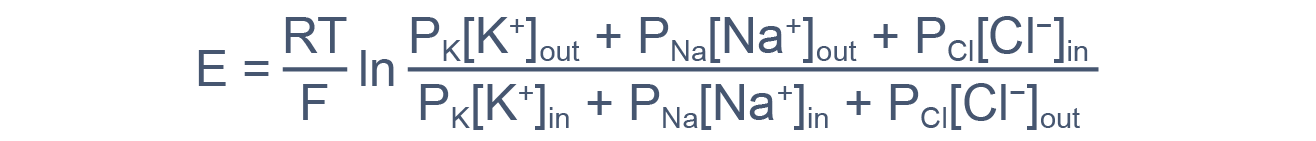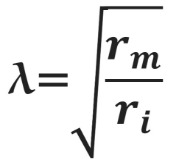Удельная электрическая емкость мембраны аксона равна

---

Подборка по базе: Судебное решение для курсовой.docx, ПР№1 Решение.docx, 1 Планируемые изменения инфраструктуры.docx, Дело 12-0272_2021. Решение по жалобе_протесту на постановление (, Квадратные уравнения. Решение неполных кв.ур..ppt, !!! готовое решение задач с формулами.doc, Бухгалтерский баланс ЗАО Стэк и решение.docx, Готовое решение_ Как произвести увольнение работника по медицинс, ОБОБЩЕНИЕ ПО ТЕМЕ Изменения с вещвами.docx, раздаточный материал к уроку решение задач на дроби.docx

---

1.Термодинамической системе было передано тепло в количестве 140 Дж, а также над ней была совершена работа в 65 Дж. Как изменилась внутренняя энергия системы в этом процессе?

Дано: Q=140 Дж. A=65 Дж. Найти: dU=?

Решение: Запишем формулу изменения внутренней энергии:

Где A — работа совершенная над газом (Работа внешних сил), Q — кол-во теплоты, переданное данной системе. Осталось посчитать:

dU=140+65=205 Дж=0.205кДж.

Ответ: dU=0.205кДж

2. Определите калорический коэффициент кислорода при окислении глюкозы, если из экспериментов с калориметрической бомбой известно, что при окислении 1 г глюкозы выделяется 15,7 кДж теплоты.

Задача 3. Сколько полезной работы может быть получено при сжигании 12*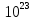 молекул глюкозы, если предположить, что тело человека работает как тепловая машина с КПД 50%?

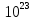
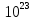
Дано: V = 12* / 6,022* = 2 моль n=50%=0.5 КПД
Найти- А (полезную)
Решение: Теплота сгорание глюкозы Q=2800 кДж/моль. согласно справочнику
КПД (n) = A Q *100%

Na=Число Авогадро 6,022*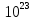
Q- Количество теплоты полученное рабочим телом от нагревателя
А — полезная работа, совершаемая рабочим телом за цикл
Тогда A=nQV=0,5*2800*2=2800 кДж.

Ответ: 2800 кДж.

4. Спортсмен, пробегая дистанцию, выделяет за 1 мин 90 л воздуха, в котором содержится
12% кислорода и 8% углекислого газа. Каков расход энергии спортсмена за 5 мин
дистанции?

Дано: t1=1час, V=90л, VO2=12%, VCO2=8%, t2=5 мин
Найти: E-?
Решение: В 100мл 21% O2 и 0,003 CO2
Расход O2 на 100мл VO2= 21-12=9%=9мл O2
Расход CO2 на 100мл VCO2=8%=8мл CO2
ДК-дыхательный коэффициент ДК= VCO2/ VO2=8/9=0,88
КК-калорический коэффициент ДК=0,88=КК=20,515 кДЖ
В 100мл – 9 мл В 90000мл- Хмл
Х=90000 х 9/100= 8100мл
За 1 минуту 1000 мл – 20,515кДЖ
8100мл- Х
Х= 20,515 х 8100/1000=166кДЖ
За 5 минут Е=166кДЖ х 5= 830кДЖ
Ответ: Е= 830 кДЖ

5. Удельная электрическая емкость мембраны аксона, измеренная внутриклеточным микроэлектродом, оказалась равной 0,5 мкФ/см^2. По формуле плоского конденсатора оценить толщину гидрофобного слоя мембраны с диэлектрической проницаемостью равной 2.

Дано: C=0,5 мкФ/см^2 E=2
Найти: h-?
Решение: C=Eo*E*S/h-выражение для емкости плоского конденсатора, где С-емкость
Е-относительная диэлектрическая проницаемость
Ео=8,85*10^-12 Ф/м-диэлектрическая постоянная
S-площадь обкладки конденсатора (мембраны аксона)
h-толщина гидрофобного слоя мембраны
Cуд.=C/S=0,5*10^-6/(10^-2 м)^2=0,5*10^-2 Ф/м^2
Е=Ео/Е>1
выражаем h:
h=EoES/C=EoE/Cуд.= 2*8,85*10^-12/0,5*10^-2=35,4*10^-10=3,5 Нм
Ответ: 3,5 Нм 

6. Используя уравнение Эйнштейна Sкв = 2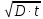 ; где D — коэффициент латеральной

диффузии, определите, какое расстояние на поверхности мембраны эритроцита проходит

молекула фосфолипида за 1 секунду в результате латеральной диффузии? D принять равным 10-

12 м^2с.Сравните с окружностью эритроцита диаметром 8 мкм.
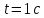
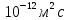
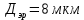
Дано: D = Найти : l За 1 сек. -?

Решение:

Sкв = 2

Sкв=2 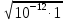= 2

l) (длина окружности)=2ПR=2Пd (п-число пи, d-диаметр

1секунда=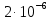 (м)

x =3.14*8

решаем пропорцию

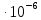
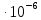
x=(3,14*8 ) / (2 )

x=12,28 с Ответ: 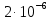(м) x=12,28c
7. Микровязкость мембраны эритроцита при температуре 37С равна 6 Пз. Найти величину коэффициента диффузии для ионов кальция. Если радиус негидратированного иона кальция 1,5 нм.
Дано: Т=37С, n=6 Пз, r=1,5 нм, k(постоянная Больцмана)=1, 38х10^-23Дж/К, число пи=3,14

Найти: D=? – величину коэффициента диффузии

Решение:

1.) Т=37С=310К, n(микровязкость)=6 Пз, k(постоянная Больцмана)=1, 38х10^-23Дж/К, r(радиус)=1,5нм, пи(число)=3,14.

3.) Найдем искомое по формуле: =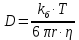

Ответ: D=

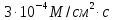
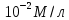
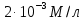
8. Бислойная липидная мембрана (БЛМ) толщиной 10 нм разделяет камеру на две части. Плотность потока метиленового синего через БЛМ постоянна и равна причём концентрация его с одной стороны мембраны равна , а с другой . Чему равен коэффициент проницаемости этого вещества через БЛМ?
Дано: h = 10 нм = 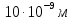J =

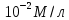
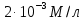
С0 = М Сi =
Найти: D-?

Решение:
Воспользуемся уравнением Фика:
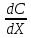
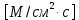
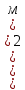
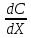
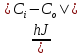
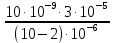
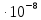
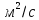
J = — D где J – плотность потока диффундирующего вещества , D – коэффициент диффузии, ]

— производная от концентрации диффундирующего вещества по направлению х (проекция градиента концентраций на направление х). C0,Ci-концентрация внутри и снаружи мембраны,

D= = = 3.75
Ответ: 3.75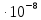

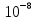
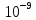
9. Концентрация глюкозы в клетке равна моль/л, а вне клетки моль/л. Температура 20’С. Найти приращение химического потенциала при транспорте 10 моль глюкозы в клетку и из клетки.

Дано:

[Гл]_i=10^-8 моль/л [Гл]_o=10^-9 моль/л T=20^о C=293К N=10 моль

Найти: Δµ (в клетку) Δµ (из клетки)

Решение: µ=µ₀+RT*lnC

µ-химический потенциал, Дж/моль µ_о-стандартный химический потенциал, Дж/моль

R=8,3 – газовая константа, (Дж/(моль*К) T_(к)-температура С [число молей]-концентрация

В клетку: Δµ=µ_о-µ_i=µ_0o+RT*lnC_o-µ_0i + RT*lnC_i=RT*ln(C_o/C_i)=8,3*293*ln(10^-9/10^-8)=-2432*2,3lg10=-5594 [Дж/моль]

-5,6 [кДж/моль] < 0 (Пассивная диффузия)

Из клетки: Δµ=µ_i— µ_о= µ_0i+RT*lnC_i — µ_0o+RT*lnC_o=8,3*293*ln(10^-9/10^-8)=2432*2,3lg10=5594 Дж/моль5,6 кДж/моль>0 (Только активный транспорт)

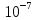
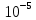
10. Найти приращение электрохимического потенциала при транспорте кальция из клетки и в клетку, если концентрация кальция в клетке равна моль/л, вне клетки моль/л, при температуре 20С. Величина мембранного потенциала (-60)мВ

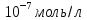
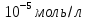
Дано: Ci(Ca)= Co(Ca)=
T=20C=293K L(фи)=(-60)мВ
Найти:
u1-? u2-?
Решение: u=R•T•ln•(-Co/Ci) +ZF(Lo+L1)
u- химический потенциал
R=8,3 [Дж/моль•К] газовая постоянная
F= постоянная Фарадея
Z= 2 валентность ионов
Со=внеклеточная концентрация иона
Сi= внутриклеточная концентрация иона

M=Mo+R•T•ln 10-5/10-7 + 2•9,6 •60= 8,3•293• ln 10^2 +2•9,6•60=11186,74+1152=
12338,7 Дж/моль=12,3 КДж/моль. 

11. Концентрация ионов натрия в клетке 1 ммоль/л, вне клетки 180 ммоль/л. Разность потенциалов на мембране (- 80 мВ). Можно ли осуществить активный транспорт ионов натрия при помощи натрий-калиевого насоса из клетки на наружную поверхность мембраны, при температуре 37 С, изменение свободной энергии при гидролизе 1 моль АТФ = (- 45) кДж/моль, КПД насоса 50%.

Дано: {Na}i= 1мМ {Na}o=180 мМ t=37

Разность потенциалов 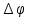= -80мВ 1М(Атф)= -45 кДж/моль КПД=50%

12. Концентрация глюкозы в плазме крови 3,5 мМ/л, концентрация глюкозы в

эритроците 5 мМ/л. Концентрация ионов Na+ в эритроците 4 мМ/л, а в плазме 140

мМ/л, температура 37С. Можно ли транспортировать молекулу глюкозы в

эритроцит, используя вторичный активный транспорт. Разность потенциалов на

мембране эритроцита (-60) мВ.

13. Какое количество одновалентных ионов нужно переместить на наружную поверхность мембраны из клетки, чтобы сохдать потенциал покоя 120мВ? Площадь поверхности мембраны 10-9 м2, удельная электроёмкость мембраны Суд=10-2 Ф/м2.

Дано: 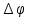=120мВ; S=10-9м2; Суд=10-2Ф/м2;

Решение:

-потенциал покоя; S-площадь поверхности мембраны; Суд-удельная электроёмкость

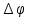
1. С=Суд*S=10-2*10-9=10-11Ф — электроёмкость мембраны.

2. Заряд поверхности мембраны находим через ёмкость: q=C*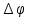 =10-11*0,12=10-12Кл.

3. Число ионов, образующих такой заряд, рано n=q/e=10-12/1,6*10-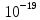 =6,2*106.

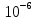
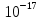
Ответ: n=6,2* ; моль ионов.

14. Найдите, какой должна быть концентрация ионов калия в клетке, при которой
величина равновесного калиевого потенциала равна (-100) мВ, при температуре 37оС,
[K+]o = 6х10-3 моль/л

Дано:

Найти: Сi — ?

Решение:

моль/л

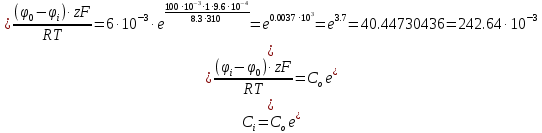
15. Определите равновесный мембранный потенциал при отношении концентраций

натрия снаружи и внутри а) 1:1; б) 10:1; в) 100:1, температура Т = 310 К

Дано:

[Na+]o/[Na+]i=1/1

[Na+]o/[Na+]i=10/1

[Na+]o/[Na+]i=100/1

T=37°C

Найти:

 Дельта фи 
Решение:

(Фи) yi-yo=RT/ZF•ln[Na+]o/[Na+]i
R- 8,3 [дж/моль•К°] газовая константа 

T[К°]- температура 

Z[1]- валентность иона

F-  9,6•10^4 [кл/моль]

yi-yo- равновесный потенциал [B]
RT/ZF=8,3•310/1•9,6•10^4=268•10^4=268•10^1•10^-3=27[мВ]

а)yi-yo=27ln1/1=0 [мВ]

б)yi-yo=27ln10/1=27•2,3lg10=62 [мВ]

в)yi-yo=27ln100/1=27•2,3lg10^2=124 [мВ]

16. Чему равна напряженность электрического поля на мембране в состоянии покоя,

если концентрация ионов калия внутри клетки 125 ммоль/л, снаружи – 2,5 ммоль/л, а

толщина мембраны 8 нм?
Дано:[К+]i=125 ммоль/л [К+]о=2,5 ммоль/л

h=8 нм=8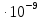 м

Найти: Е-?
Решение:

Е= — (Фi-Фо)/h

Фi-Фо=RT/ZF * ln(Co/Ci)

Фi-Фо= ((8,31*310)/(1*96485)) * ln ((2.5*10^-3)/(125*10^-3))=-0,105 Вольт

Е= (0,105/8*10^-9)= 0,013 *10^-9 В/м

*Пояснения*

Е — напряжённость эл.поля

Фi-Фо разность потенциалов

h — толщина мембраны

R- газовая постоянная(8,31дж/моль*К)

Т — температура (310 К)

С- концентрация
17. Определите равновесный мембранный потенциал митохондрий, если при 37 ͦС внутри митохондрий pH=9, а в окружающей среде рН=7.
Дано: T=37°C = 310 K
pH(i) = 9 pH(o)= 7
Найти:
∆(фи)=?
Решение:
Равновесный мембранный потенциал можно рассчитать с помощью формулы Нернста:
1) ∆(фи) = (фи i) — (фи o) = RT/ZF * Ln C(o)/C(i),
где (фи i) — потенциал на внутренней части мембраны, (фи o) — потенциал на внешней части мембраны, R — газовая постоянная, Т-температура, Z- валентность ионов, F — постоянная Фарадея, Со-концентрация ионов снаружи клетки, Сi- концентрация ионов внутри клетки.
Водородный показатель рН определяется как
2) рН=-lg[H^+],
где величина [Н^+] имеет размерность моль/л и по своей сути является концентрацией. Вычислим концентрацию протонов (ядер атомов водорода) по величине рН:
3) C=[H^+]=10^-pH.
Тогда объединение (1) — (3) позволяет записать:
4) ∆(фи) =RT/ZF * ln * 10^-pHo / 10^-pHi ==RT/ZF * ln * 10^pHo / 10^pHi =RT/ZF * ln * 10^(pHi — pHo) = RT/ZF*(pHi — pHo) * ln10
Подставим числа в выражение (4) :
∆(фи) =(8.31 Дж/моль*К * 310 К / 1*96500Кл/моль ) *(9-7) ln10=0,123 Дж/К =123мВ
Ответ: ∆(фи) = 123 мВ

18. Рассчитайте амплитуду потенциала действия нервного волокна при следующих
концентрациях ионов: К+ i = 15510-3моль/л, К+о = 410-3моль/л, Na+i = 12 10-
3моль/л, Na+o = 145 10-3моль/л, температура Т = 310 К.

19. Определите среднюю силу, действующую на барабанную перепонку уха человека !!!! (была 3, которая неправильная)

(площадь S = 66 мм2) для двух случаев: а) порог слышимости; б) порог болевого

ощущения. Частота равна 1кГц.

Дано: S=66мм²; n=1кГц

Найти: F₀-?; F_бол-?

Решение:

I=ΔP²/(2p(

ро)V) I-интенсивность; P-плотность среды; p(ро)-плотность среды; V-скорость звука

I₀=10^-12 Вт/м² — Р₀=20*10^-5Па

I_б=10 Вт/м² — Р_б=60Па

L_р=20lg P/P₀ (дБ)

P=F/S

F₀=P₀S=2*10^-5*66*10^-6=132*10^-11=1,32*10^-9Н=1,32мН

F_б=P_бS=60*66*10^-6=3960=3,96*10^-3Н=3,96мН

Ответ: F₀=1,32мН; F_б=3,96мН
20. Уровень громкости звука частотой V(ню) = 5000 Гц равен Е = 50 фон. Найдите

интенсивность этого звука.

Дано: V(ню)=5000Гц; Е=50 фон

Найти: I=? (Вт/м²)
Решение: V(ню) – частота, Е – уровень громкости звука, I – интенсивность звука, I₀ – порог слышимости, L – уровень интенсивности
Е=10 Lg I/I₀ (фон), т.к. V ≠1000 Гц, то используем изофоны
1) L=52 дБ
L=10 Lg I/I₀
Lg I/I₀ = L/10
I/I₀ = 10 ^L/10
I = I₀ *10 ^L/10
I = 10^-12 * 10^52/10 = 10^-6.8 Вт/М²
Ответ : 10^-6.8 Вт/М²

21. Шум на улице, которому соответствует уровень интенсивности звука L1 = 50 дБ,

слышен в комнате так, как шум L2 = 30 дБ. Найдите отношение интенсивности звука на

улице и в комнате.
Дано: L1= 50 дБ = 5 Б, L2= 30 дБ=3Б.

Найти: I₁/I₂=?
Решение: L1= lg I₁/I₀ ; L2= = lg I₂/I₀
L-уровень интенсивности (дБ), I – интенсивность (Вт/м²), I₀ – порог слышимости = 10^-12 Вт/м²
5 = lg I₁/I₀ 3=lg I₂/I₀
I₁ = I₀ * 10⁵ I₂ = I₀ *10³
10⁵/10³ = 100
Ответ : 100

22. Отношение интенсивностей двух источников звука равно: I2/I1=4. Чему равна

разность уровней интенсивностей этих звуков?

Дано: I₂/I₁=4 .

Найти: L2-L1 -?
Решение:

L=10lg I/I₀
L-уровень интенсивности (дБ), I – интенсивность (Вт/м²), I₀ – порог слышимости = 10^-12 Вт/м²
L2-L1=10lg I₂/I₀ – 10lg I₁/I₀= 10 (lg I₂ –lg I₀ – (lg I₁ – lg I₀))= 10(lg I₂ – lg I₁)= 10 lg I₂/I₁= 10 lg 4 ≈6
Ответ: 6 (дБ?)

23. В лабораторном цехе уровень интенсивности шума достигла 80 дБ. С целью

уменьшения шума было решено обить стены этого помещения материалом поглощающим

звук, который уменьшает интенсивность звука в 1000 раз. Какой уровень интенсивности

шума станет после этого в этом помещении?

Дано: L1=80дБ ;

Найти: L2-?

Решение: определим интенсивность звука

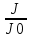
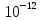
L1=10lg , где J0-условный нулевой уровень интенсивности звука(J0= Вт/м^2)

При изменении интенсивности звука изменение уровня интенсивности будет равно:

Ответ: 50дБ

24. Скорость пульсовой волны в артериях составляет 8 м/с. Чему равен модуль

упругости этих сосудов, если известно, что отношение радиуса просвета к толщине стенки

сосуда равное 6, а плотность сосудистой стенки равна 1,15 г/см3.

Дано: V=8м/с; р

(ро)=1,15г/см Найти: I₁/I₂=?
Решение: L1= lg I₁/I₀ ; L2= = lg I₂/I₀
L-уровень интенсивности (дБ), I – интенсивность (Вт/м²), I₀ – порог слышимости = 10^-12 Вт/м²
5 = lg I₁/I₀ 3=lg I₂/I₀ I₁ = I₀ * 10⁵ I₂ = I₀ *10³
10⁵/10³ = 100
Ответ : 100

25. Какова должна быть разность давлений Р на концах капилляра радиуса r = 1 мм и

длины L = 10 см, чтобы за время t = 5 с через него можно было пропустить объем V = 1

см3 воды (коэффициент вязкости η1 = 10-3 Па·с) или глицерина (η2 = 0,85 Па·с)?

Дано: r =1мм= 10¯³м, L=1см=0,1м, t=5с, V=1см³=1·10¯⁶м³, ŋ1=10¯³Па·с, ŋ2=0,85Па·с

Найти: ∆Р-?

Решение: Q=∆Р/x

t-время, ŋ-вязкость, x-гидравлич сопротивление, Q- обьем, L-длина, R-радиус

26. Наблюдая под микроскопом эритроциты в капилляре, можно измерить скорость

течения крови: υ1 = 0,5 мм/с. Средняя скорость тока крови в аорте составляет υ2 = 40 см/с.

На основании этих данных определить, во сколько раз суммарная площадь сечений

функционирующих капилляров больше площади сечения аорты.

Условие неразрывности струи было получено для трубки тока переменного сечения

Дано: V_кап=0,5мм/с; V_{аорт.средн}=40см/c;

Найти: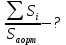

Решение:

27. При атеросклерозе, вследствие образования бляшек на стенках сосуда, критическое

значение числа Рейнольдса может снизиться до 1160. Определить скорость, при которой

возможен переход ламинарного течения крови в турбулентное в сосуде диаметром 2,5 мм.

Плотность крови 1050 кг/м3, вязкость крови 5. 10-3Па·с.

Дано: d=2,5мм=2,5·10¯³м, ρ=1050кг/м³, ŋ=5·10¯³Па·с, Re=1160

Найти: Vперехода-?

Решение: ρж-плотность жидкости,Vпер-скорость перехода, D-диаметр сосуда, ŋ-коэф вязкости

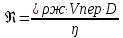
28. Во сколько раз изображение предмета на сетчатке глаза меньше самого предмета,

находящегося на расстоянии 30 м от наблюдателя? Фокусное расстояние оптической

системы глаза принять равным 1,5 см.

Дано: а=30 м; F=1,5 см

Решение:

H F

а h

Из рисунка следует ,что изображение будет перевернутым, уменьшенным и действительным.

Составим пропорцию:

Ответ: Изображение предмета на сетчатке глаза меньше самого предмета в 2000 раз
29. При максимальной аккомодации радиус кривизны передней поверхности

хрусталика изменяется от 10 до 5,5 мм, задней – соответственно от 6 до 5,5 мм. На

сколько, при этом увеличится оптическая сила хрусталика. Показатель преломления

хрусталика 1,424, в окружающей среде 1,336.

Дано: R₁=10mm; R₁¹=5,5mm; R₂=6mm; R₂¹=5,5mm; n_хр=1,424; n_ср=1,336

Найти:

Решение: при максимально аккомодации изменяется кривизна хрусталика. Он становится более выпуклым(F уменьшается) и его оптическая сила возрастает т.е. D₂>D₁

Оптическая плотность линзы вычисляется по формуле: D=(n_1;2-1)(± )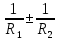

D-оптическая сила [ ]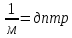

R₁ и R₂— радиусы кривизны ограничивающих сферических поверхностей.

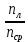
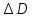
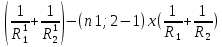
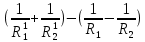
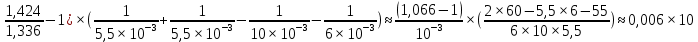
n_1;2 = – относительный показатель преломления для вещества лизны отностительно окр.среды. знак + берется для выпуклой поверхности. а- для вогнутой, т.к. хрусталик двояко выпуклая линза, обе кривизны положительного знака

= D₂-D₁=(n_1;2-1)x = (n_1;2-1)x =( ³ 6 дптр

Ответ: при максимальной аккомодации оптическая сила хрусталика увеличена примерно на 6 дптр

30. Показатели преломления двух сред равны 1,5263 и 1,1275. Найти предельный угол преломления.

Дано: n1=1.5263 n2=1.1275

Найти: ?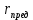

Решение:

закон преломления света Ф. Снеля

r-угол преломления, i-угол падения, n1 – показатель преломления 1 среды, n2 — показатель преломления 2 среды

Выразим: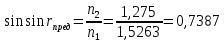

Ответ:

31. Оптическая сила линзы составляет 5 дптр. Чему равно фокусное расстояние линзы?

Дано: D=5 дптр. Найти: F -?

Решение: 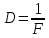– оптическая сила

Ответ: 20cm фокусное растояние линзы
32. Оптическая сила хрусталика для человека с нормальным зрением равна 25 дптр.

Показатель преломления 1,4. Вычислите радиусы кривизны хрусталика, если известно,

что один радиус кривизны в 2 раза больше другого.

Дано: D = 25 дптр N = 1,4 R2= 2R1

Найти: R1 — ? R2 — ?

Решение: Хрусталик можно считать тонкой линзой, поэтому для него будет справедлива формула тонкой линзы 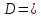(n-1)(

Где D – оптическая сила хрусталика F – фокусное растояние n – относительный показатель преломления хрусталика, R1 и R2 – радиусы кривизны поверхностей хрусталика.

Используя условие задачи R2=2R1, получаем

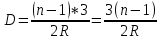
R2=2.4*2=4.8мм
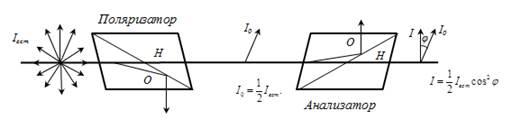
33. Чему равен угол между главными плоскостями поляризатора и анализатора, если интенсивность естественного света, прошедшего через эти призмы, уменьшилась в 4 раза? Поглощением света пренебречь.

Дано:

Найти: -?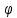

Решение:

Закон Маллюса

I_ана-интенсивность поляризованного света прошедшего анализатор

I_пад-интенсивность поляризованного света падающего на анализатор

-угол между плоскостями поляризации поляризатора и анализатора

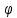
Интенсивность естественного света, прошедшего поляризатор, уменьшается в 2 раза, то есть

Ответ:45

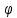
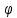
34. Главные плоскости двух призм Николя, поставленных на пути луча, образуют между собой угол 1=60°. Как изменится интенсивность света, прошедшего через эти призмы, если угол между их плоскостями поляризации станет равным 2=300?

Дано: φ1=60°, φ2=30°
Найти: как изменится интенсивность света?
РЕШЕНИЕ: 1) I (прош)=I под cos²φ
2) a = I прош / I под = cosφ1
b = I прош / I под = cosφ2
3) b/a= cos²φ2 / cos²φ1 = cos²20/ cos²60 = ( )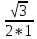
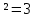
ОТВЕТ: Интенсивность света, прошедшего через призмы, если угол между их плоскостями поляризации станет равным φ2=30° увеличившись в 3 раза.
35. Коэффициент пропускания раствора τ=0,3. Чему равна его оптическая плотность? Если известна оптическая плотность раствора D=0,08, чему равен коэффициент пропускания?
Дано: T=0.3 D=0.08 Найти: D=?

Решение: 1) D=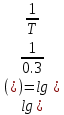 )=0.522

2) 0,08=lg(

T-коэффициент пропускания

D-оптическая плотность

Ответ: оптическая плотность раствора 0,83

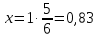
36. Чему равен молярный показатель поглощения вещества, если при прохождении света через раствор с концентрацией 0,5 моль интенсивность света уменьшилась в 10 раз? Длина кюветы 0,3 см.
Дано: С=0,5 моль l=0,3 см Найти: Е-?

Решение: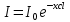

Оптическая плотность раствора или вещества это отношение падающего и преходящего света

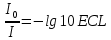
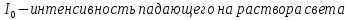
lg I-интенсивность света проходящего через раствора

Е – молярный коэф.поглощения

С – Концентрация окрашенного вещества, моль/л

l-длина кюветы

lg10=E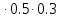

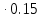
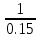
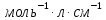
1=E E= =6.7

Ответ: Молярный показатель поглощения вещества Е=6.7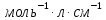

37. Найдите границу тормозного рентгеновского излучения (частоту и длину волны) для напряжений и1=2 кВ и и2=20 кВ. Во сколько раз энергия фотонов этих излучений больше энергии фотона, с длиной волны λ =760 нм.

Эксперимент показывает, что приложенное к регненовской трубке напряжение U, связано с длинной волны λ

λ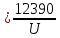 где λ – в ангстремах, U – в вольтах.

Частоты для этих длин волн:

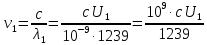
C – скорость света.

Теперь сравним энергии фотонов с длинами волн

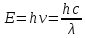
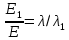
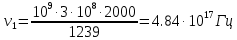
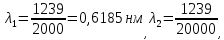
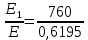
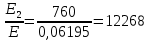
Энергия фотона h- постоянная планка, ν – частота

= 0,06195 нм

=1226,8

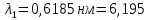
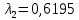
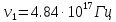
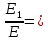
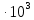
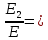
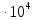
Ответ: длины волн Å Å,

1,23 1,23
38. Найдите поток рентгеновского излучения при разности потенциалов на

рентгеновской трубке 15 кВ и силе тока 3 мА. Анод изготовлен из вольфрама. Скольким

фотонам в секунду соответствует этот поток, если допустить, что излучается

электромагнитная волна, длина которой равна 1/2 от длины волны, соответствующей

границе спектра тормозного рентгеновского излучения.

Поток Ф излучения от ренгеновской трубки починяется соотношению:

где, k= ,I-сила тока,U-напряжение между электродами, Z – порядковый номер элемента анода. Количество N фотонов, которым соответствует длина , при частоте ν

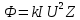
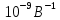
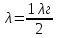
N=Ф/hν , где h – постоянная планка. Связь частоты с длиной волны имеет вид

ν=с/λ , где с – скорость света

N = Фλ/hc =>

=>

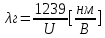
Ответ: поток 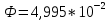Дж, число фотонов

39. Мощность экспозиционной дозы γ-излучения на расстоянии R = 1 м от точечного источника составляет р=2,15*10^-7 Кл/кг. Определите минимальное расстояние от источника, на котором можно ежедневно работать по 6 ч без защиты. Предельно допустимой эквивалентной доз при профессиональном облучении считать 5*10-2 Дж/кг в течение года. Поглощение γ -излучения воздухом не учитывать.

I – интенсивность электромагнитных волн

А – активность элемента Е – энергия порции излучения R – радиус сферы

Далее можно посчитать величину заряда в слое толщиной 1 см

. =>

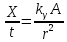
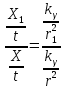
Следовательно, мощность экспозиционной дозы

Тогда

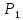
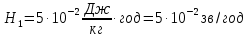
Величина за год определяется значением эквивалентной дозы

, переведем зиверты в греи

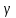
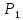
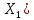
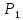
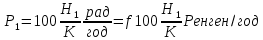
Тут К=1, так как в условии задачи сказано об источнике -излучения, далее нужно перевести величина в дозу экспозиционную ( . Если мощность дозы выражена в радах/год, то в случае мягких тканей её значение числено будет равно ренгенам/год. Так как на данный момент размерность Грей, нужно умножить

Где f = 1

Возьмем р=2,15*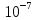 Кл/кг. За секунду, Так как 1кл/кг = 3876 Р, поэтому за 1 год

Ответ: нужно удалиться от источника 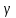-излучения на расстояние около 36 метров чтобы безопасно работать по 6 часов в день без использования защитного костюма

40. Какова активность препарата, если в течение 10 мин распадается 10 000 ядер этого вещества?

По определению активностью препарата называется число распавшихся ядер за единицу времени (секунду, минуту, час). Если препарат имеет период полураспада больше суток, то можно считать, что количество распадов за единицу времени остается постоянным, при недолгом наблюдении за препаратом. Тогда искомая активность А будет равна

Где ∆N – число распавшихся атомов за время ∆t

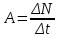
Ответ: активность препарата А = 16,7 Бк.

41. Работа выхода электрона из лития А = 2,5 эВ. Будет ли фотоэффект при освещении

лития монохроматическим светом с длиной волны 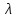= 50 нм?

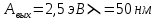
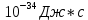
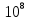
Дано: h = 6,6* С = 3* м/c

Найти: Будет ли фотоэффект?

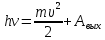
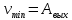
Решение: h h

Ответ: λ<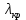 Да, будет

Вы в первый раз на нашем сайте?

Для входа нужно использовать логин и пароль от личного кабинета ВУЗа http://www.kstu.ru/ds/eu_21.jsp?id=0

На данном сайте ваши пароли не хранятся, т.к. используется единая система управления доступом ВУЗа (LDAP-сервер), Менять пароли и восстанавливать нужно через личный кабинет http://www.kstu.ru/ds/eu_21.jsp?id=0

Вопрос
23.Назовите метод, с помощью которого
можно изучать подвижность липидных
молекул в

мембране.

Варианты
ответа:

1.
Электронная микроскопия.

2.
Дифракция рентгеновских лучей.

3.
Флуоресцентный анализ

4.
Электронный парамагнитный резонанс
(ЭПР).

Электронный парамагнитный резонанс (эпр).

Вопрос
24.Какие физические методы, из перечисленных
ниже, пригодны для оценки фазового

состояния
липидов в мембране?

a)
Дифракция рентгеновских лучей.

b)
Флуоресцентный анализ

c)
Электронная микроскопия.

d)
Электронный парамагнитный резонанс
(ЭПР).

Варианты
ответа:

1.
a,c,d

2.
a,c

3.
b,c,d

4.
b,d

a,c,d

Вопрос
25.Характерное время переноса молекулы
фосфолипидов из одного положения
равновесия в другое при их диффузии:

Варианты
ответов: Флип-флоп

1.
Примерно 1 час

2.
10-7-10-8 с

3.
10 – 50 с

Примерно 1 час

Вопрос
26. При фазовом переходе мембранных
фосфолипидов из жидкокристалли-ческого
состояния

в
гель толщина бислоя изменяется. Как при
этом изменяется электрическая ёмкость

мембраны?

Варианты
ответа:

1.
Увеличивается

2.
Уменьшается

3.
Увеличивается в несколько раз

4.
Уменьшается в несколько раз

Уменьшается

Вопрос
27. Где вязкость выше: у поверхности
мембраны или в её центре?

Варианты
ответа:

1.
В центре

2.
У поверхности

У поверхности

Вопрос
28.Удельная электрическая ёмкость
мембраны аксона:

Варианты
ответа:

1.
0,5.10-4 Ф/м2 3. 0,5.10-2 Ф/см2

2.
0,5.10-2 Ф/м2 4. 0,5.10^-12
Ф/м2

0,5.10^-12
Ф/м2

Вопрос
29.Как влияют белки на фазовые переходы?

Варианты
ответа:

1.Увеличивают
температуру фазового перехода.

2.
Уменьшают температуру фазового перехода.

3.
Не влияют на температуру фазового
перехода.

Не
влияют на температуру фазового перехода.

Вопрос
30.Какими способами можно измерить
фазовые переходы или установить
критическую температуру?

Варианты
ответа:

1.Электронная
микроскопия.

2.Дифракция
рентгеновских лучей.

3.
Дифференциальная калориметрия.

4.Электронный
парамагнитный резонанс (ЭПР).

Дифференциальная
калориметрия.

Вопрос
31.В чём заключается основная роль
актиновых микрофиламентов в клетке?

Варианты
ответов:

1.
поддержание и адаптация формы клетки
ко внешним воздействиям,

2.
обеспечивают активный внутриклеточный
транспорт

Поддержание
и адаптация формы клетки ко внешним
воздействиям,

Вопрос
32.Назовите авторов, которые предложили
белково-кристаллическую модель
строения
биологических мембран.

Варианты
ответа:

1.
В 1925 году Гортер и Грендел

2.
В 1935 году Ф. Даниэлли и Г. Доусон

3.
В 1966 году Ленард и С. Сингером

4.
В
1970 году
G. Vanderkooi, D. Green

В
1970 году
G. Vanderkooi, D. Green

Вопрос
33.Назовите метод, с помощью которого
можно оценить микровязкость липидной
фазы

мембраны.

Варианты
ответов:

1.
Электронная микроскопия.

2.
Дифракция рентгеновских лучей.

3.
Флуоресцентный анализ

4.
Электронный парамагнитный резонанс
(ЭПР).

Электронный
парамагнитный резонанс (ЭПР).

Вопрос
34.Продолжите фразу «Высокая подвижность
липидных молекул обусловливает движение
…

Варианты
ответов:

1.
вокруг центра симметрии фосфолипида.

2.
вдоль поверхности мембраны.

3.
флип-флоп.

флип-флоп.

Вопрос
35.Назовите метод, с помощью которого
была определена скорость перескоков
молекул с

одной
поверхности мембраны на другую.

Варианты
ответов:

1.
Дифракция рентгеновских лучей.

2.
Флуоресцентный анализ.

3.
Метод спиновых меток.

4.
Электронный парамагнитный резонанс
(ЭПР).

Метод
спиновых меток.

Вопрос
36.При фазовом переходе мембранных
фосфолипидов из жидкокристаллического
состояния в гель толщина бислоя
изменяется.

Как
при этом изменяется напряжённость
электрического поля в мембране?

Варианты
ответа:

1.
Увеличивается

2.
Уменьшается

3.
Увеличивается в несколько раз

4.
Уменьшается в несколько раз

Увеличивается

Вопрос
37.Толщина биологической мембраны

Варианты
ответа:

1.
10 А0 3. 0,1 мкм

2.
10 нм 4. 10 мкм

10
нм

Вопрос
38.Фазовый переход липидного бислоя
мембран из жидкокристаллического
состояния в гель

сопровождается:

Варианты
ответа:

1.
Утоньшением мембраны

2.
Толщина мембраны не меняется

3.
Утолщением мембраны

Утолщением
мембраны

Вопрос
39. Назовите виды белков, которые не
способны создать и поддерживать белок-
мембранный комплекс.

Варианты
ответа:

1.
α-спиральные структуры

2.
амфифильные

3.
пептидные гормоны

4.
глобулярные белки

Пептидные
гормоны

Вопрос
40.Укажите сравнительные скорости
движения фосфолипидов в мембране:

Vлатеральная,
Vфлип-флоп, Vвращение.

Варианты
ответа:

1.
Vлатеральная<Vфлип-флоп<Vвращение

2.
Vфлип-флоп<Vлатеральная<Vвращение

3.
Vвращение<Vлатеральная<Vфлип-флоп

Vфлип-флоп<Vлатеральная<Vвращение

Вопрос
41. Для градиента химического потенциала
можно записать следующее уравнение –

Варианты
ответа: 3

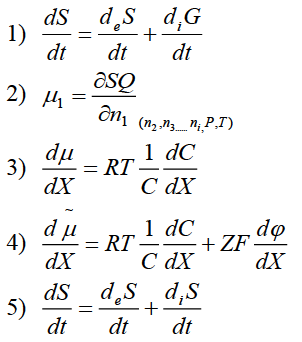
Вопрос
42. Для конечного приращения свободной
энергии системы в результате изменения

концентрации
незаряженных молекул можно записать
следующее уравнение Варианты ответа:
3

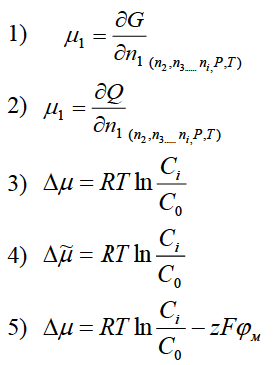
Вопрос
43. Na⁺
– Ca⁺²
обмен – это

Варианты
ответа:

1.
вторично-активный транспорт ионов Са²⁺
за счёт энергии химического потенциала
ионов Nа²⁺

2.
первично-активный транспорт ионов Са2+
за счёт энергии электрохимического
потенциала ионов Nа²⁺

3.
вторично-активный транспорт ионов Nа2+
за счёт энергии электрохимического
потенциала ионов Cа²⁺

4.
вторично-активный транспорт ионов Са2+
за счёт энергии электрохимического
потенциала ионов Nа²⁺

5.
пассивный транспорт ионов Са²⁺
и Nа²⁺

Вторично-активный
транспорт ионов Са2+ за счёт энергии
электрохимического потенциала ионов
Nа²

Вопрос
44. Активный транспорт ионов осуществляется
за счет

Варианты
ответа:

1)
латеральной диффузии молекул в мембране

2)
процессов диффузии ионов через мембраны

3)
переноса ионов через мембрану с участием
молекул-переносчиков

4)
энергии гидролиза макроэргических
связей АТФ

5)
электродиффузии ионов

Соседние файлы в предмете Биофизика

• #
• #

Химический состав живых клеток отличается от внешней среды, причем различия есть не только в сложных молекулах, таких как белки и нуклеиновые кислоты, но и в ионах. Например, во внеклеточной среде преобладают ионы натрия, а в клетке — ионы калия, причем последних на порядок больше. Сама по себе плазматическая мембрана клеток практически непроницаема для ионов, и поэтому для их переноса через мембрану существуют специальные транспортные механизмы — встроенные в мембрану белки. В геноме человека более 800 генов ионных каналов и транспортеров, а общую долю генов, вовлеченных в трансмембранный транспорт, оценивают в 10 % от всех генов, кодирующих белки^[1]. В этой серии статей мы рассмотрим механизмы трансмембранного переноса ионов и разнообразие реализуемых ими клеточных функций. Мы также уделим внимание патологиям, вызванным мутациями в генах, кодирующих соответствующие каналы и транспортеры.

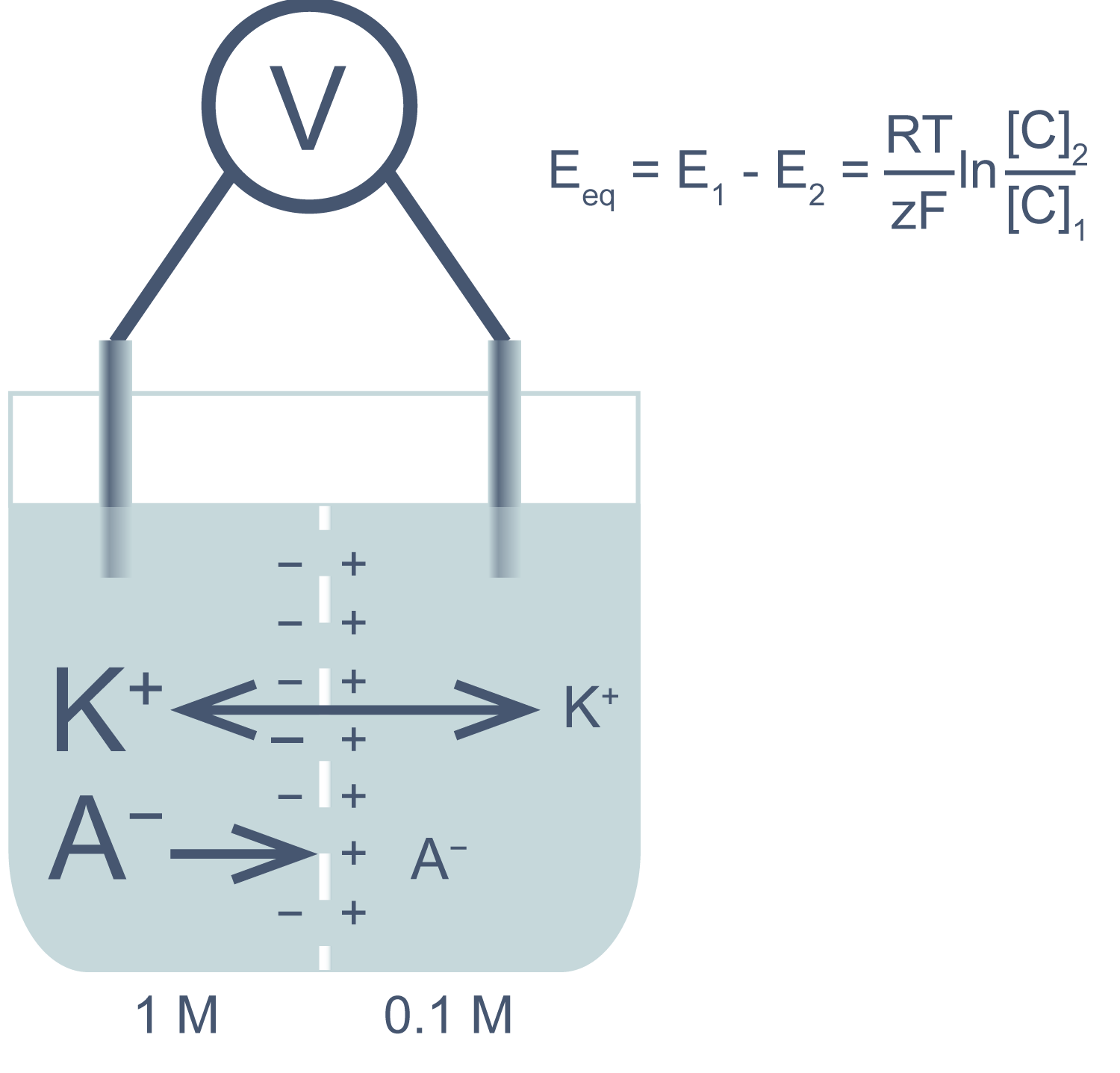
Представим себе электрохимическую ячейку — сосуд, разделенный пополам полупроницаемой мембраной, в левой части которого находится 1,0 М раствор KCl, а в правой — 0,1 М KCl. Через мембрану могут проходить катионы K⁺, но не анионы Cl⁻. Ионы K⁺ в результате процесса диффузии будут переходить из левого отсека в правый по градиенту концентрации*, тогда как ионы Cl⁻, неспособные последовать за катионами, останутся в исходном отсеке. Благодаря такому разделению зарядов на мембране будет накапливаться электрохимический потенциал: избыток анионов с левой стороны мембраны и избыток катионов с правой. Этот потенциал можно измерить, опустив в отсеки электроды, подсоединенные к вольтметру.

Асимметричный поток катионов не будет продолжаться бесконечно: накопленный электрический потенциал (с избытком положительного заряда с левой стороны мембраны) будет противодействовать диффузии ионов калия в левый отсек. Через некоторое время поток ионов K⁺ из правого отсека в левый сравняется по скорости с потоком из левого отсека в правый, и система достигнет равновесия. Для математического описания подобного равновесия применяют уравнение Нернста (рис. 1).

Рисунок 1 | Электрохимическая ячейка. V — вольтметр. Справа приведено уравнение Нернста, где E_eq — равновесный потенциал; E₁ – E₂ — разность потенциалов по обе стороны мембраны; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура (в кельвинах); F = 96485,55 Кл·моль^–1 — константа Фарадея; z — степень окисления иона (его заряд); [C]_{1, 2} — равновесные концентрации ионов по обе стороны мембраны.

Если принять, что равновесные концентрации ионов K⁺ в нашем примере равны начальным, разность потенциала на мембране при 25 °C приблизительно равна –58 мВ.

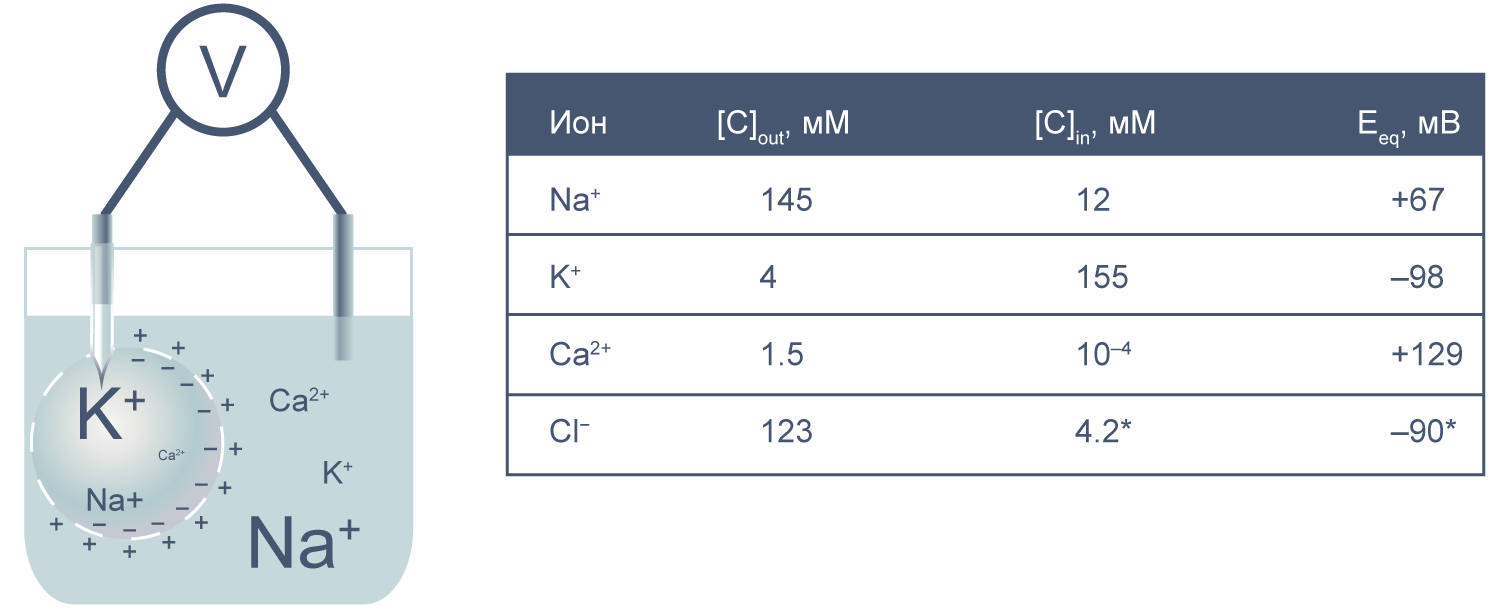
Рисунок 2 | Клетка как электрохимическая ячейка. Справа приведены концентрации основных ионов внутри и вне клетки^[2].

Теперь представим, что левая часть нашей электрохимической ячейки — это живая клетка, а правая — внешняя среда. Добавим к этой картине концентрации других физиологически значимых ионов. На мембране клетки также будет накапливаться электрохимический потенциал. Величину электрической составляющей мембранного потенциала измеряют относительно потенциала вне клетки, принимая его за ноль.

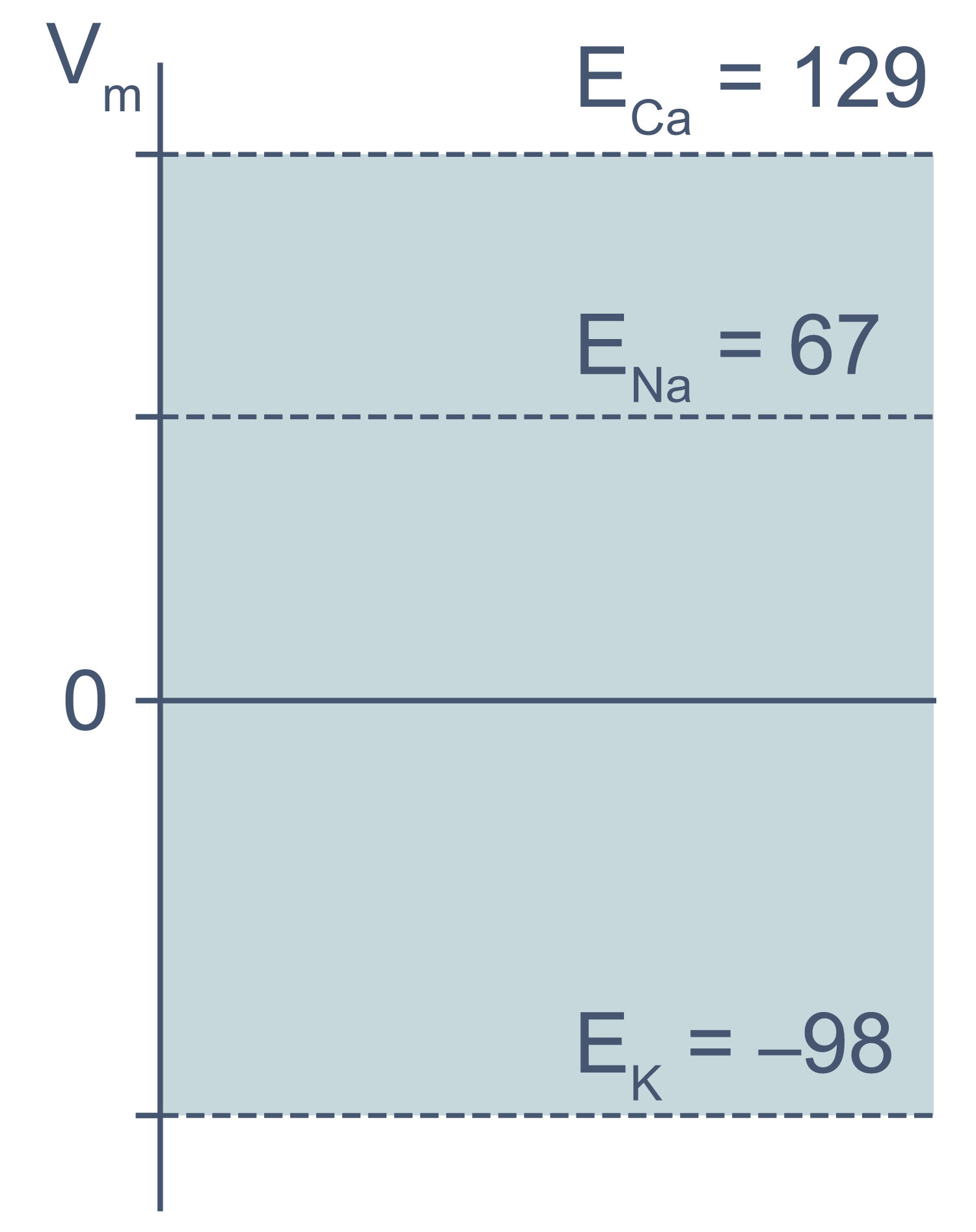
В первом приближении можно сказать, что мембрана клетки проницаема для калия и непроницаема для других катионов (Na⁺, Ca²⁺) и анионов (в первую очередь для Cl^– и отрицательно заряженных участков макромолекул). Ионы калия, выходя из клетки, создают потенциал покоя. Его величина достаточно близка к значению равновесного потенциала для K⁺, однако строго не равна ему, поскольку в реальности другие катионы и Cl^– могут участвовать в формировании потенциала покоя в различных типах клеток. Вычислив равновесные потенциалы для основных ионов, мы получим динамический диапазон величины потенциала на мембране клетки: он не может быть более отрицательным, чем E_K, и не может достигать более положительных значений на пике потенциала действия, чем E_Ca. Причина такого поведения кроется в том, что система стремится к равновесию, и при малейших отклонениях мембранного потенциала в сторону более отрицательных значений, чем E_K, K⁺ будет двигаться по электрохимическому градиенту внутрь клетки, возвращая мембранный потенциал к равновесному потенциалу для калия.

Рисунок 3 | Диапазон возможных значений мембранного потенциала от Е_K до E_Ca (показан голубым цветом).

Величина потенциала покоя зависит от типа клеток и равна около –30 мВ в невозбудимых клетках и около –80 мВ в возбудимых клетках (нейроны, мышечные и эндокринные клетки). Когда мембранный потенциал более отрицателен, чем потенциал покоя, говорят, что мембрана гиперполяризована, а когда он приближается к нулю или даже принимает положительные значения, говорят о деполяризации мембраны.

В общем случае мембранный потенциал можно вычислить согласно уравнению Гольдмана-Ходжкина-Катца, которое принимает в расчет все основные катионы и анионы:

где E — мембранный потенциал; R = 8,314 Дж/(моль·K) — универсальная газовая постоянная; T — абсолютная температура; F = 96485,55 Кл·моль^–1 — константа Фарадея; P_X — проницаемость мембраны для иона X; [C]_{in, out} — равновесные концентрации ионов внутри и вне клетки. N.B.: для анионов внеклеточная концентрация стоит в знаменателе, а внутриклеточная — в числителе.

Что же обеспечивает проницаемость мембраны для ионов? Заряженные частицы не могут самостоятельно пересекать гидрофобный внутренний слой плазматической мембраны, и поэтому требуются специальные белки, образующие гидрофильную пору, через которую ионы могут двигаться через мембрану. Такие белки называются ионными каналами. Основной вклад в поддержание потенциала покоя вносят калиевые каналы семейств K_ir (inward rectifying K⁺ channels — калиевые каналы внутреннего выпрямления) и K_2P (two—pore domain K⁺ channels — калиевые каналы с двумя поровыми доменами, которые часто называют каналами утечки), а каналы других семейств могут обеспечивать быстрое изменение мембранного потенциала в возбудимых клетках. Каналы могут селективно пропускать определенный тип ионов, например, K⁺ (как каналы семейства K_ir), или более широкий спектр веществ, как, например, коннексины — белки щелевых контактов.

Каналы бывают потенциал-зависимые (потенциал-управляемые), лиганд-зависимые, термо- и механочувствительные — в зависимости от стимула, который управляет открытием и закрытием канала. В роли стимула, таким образом, могут выступать изменения мембранного потенциала, химические агенты, температура, свет, механические и другие стимулы. Один и тот же канал может открываться под действием различных эндо- и экзогенных стимулов. Так, канал TRPV1 активируется повышением температуры более 43 °C^[3], кислым pH^[4] и разнообразными химическими веществами: капсаицином (алкалоид из перцев рода Capsicum)^[3], эндоканнабиноидом анандамидом^[5], окситоцином^[6] и др.

Физиологическая роль каналов крайне важна. К примеру, мутации в генах, кодирующих белки ионных каналов, лежат в основе патогенеза многих заболеваний человека: некоторых видов эпилепсии^[7], муковисцидоза^[8], некоторых аритмий^{[9, 10]} и др. Ионные каналы служат мишенями действия многих лекарств, ядов и токсинов.

Однако для формирования потенциала покоя недостаточно одних лишь каналов, ведь нужно создавать и поддерживать концентрационные градиенты на мембране. Основной механизм поддержания градиентов концентрации калия и натрия — это Na/K-АТФаза, фермент, за счет гидролиза одной молекулы АТФ переносящий три Na⁺ наружу и два K⁺ внутрь клетки. Она осуществляет электрогенный транспорт: в каждом транспортном цикле при переносе одного дополнительного положительного заряда наружу генерируется некоторая разность потенциалов на мембране. Чтобы оценить этот вклад Na/K-АТФазы в поддержание потенциала покоя, можно заблокировать работу фермента алкалоидом оубаином. Тогда мембрана деполяризуется примерно на 10 мВ^[11].

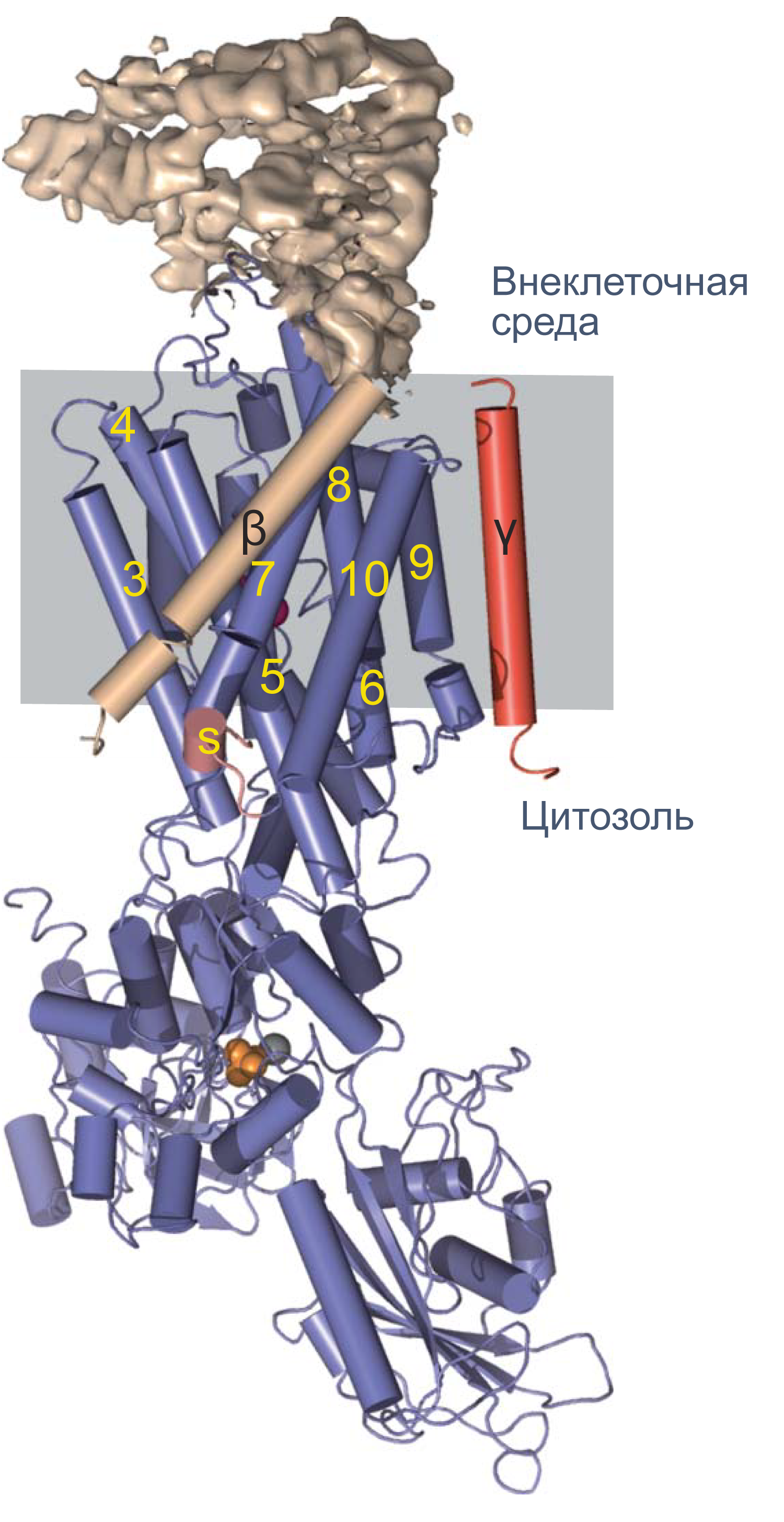
Рисунок 4 | Структура Na/K-АТФазы, полученная методом рентгеновской кристаллографии. Синим цветом показана α-субъединица, красным — γ-субъединица; β-субъединица показана бежевым цветом. Внеклеточная часть β-субъединицы показана в виде электронной плотности. Альфа-спирали изображены цилиндрами, бета-слои — плоскими стрелками^[12].

Активный и пассивный транспорт веществ через мембрану

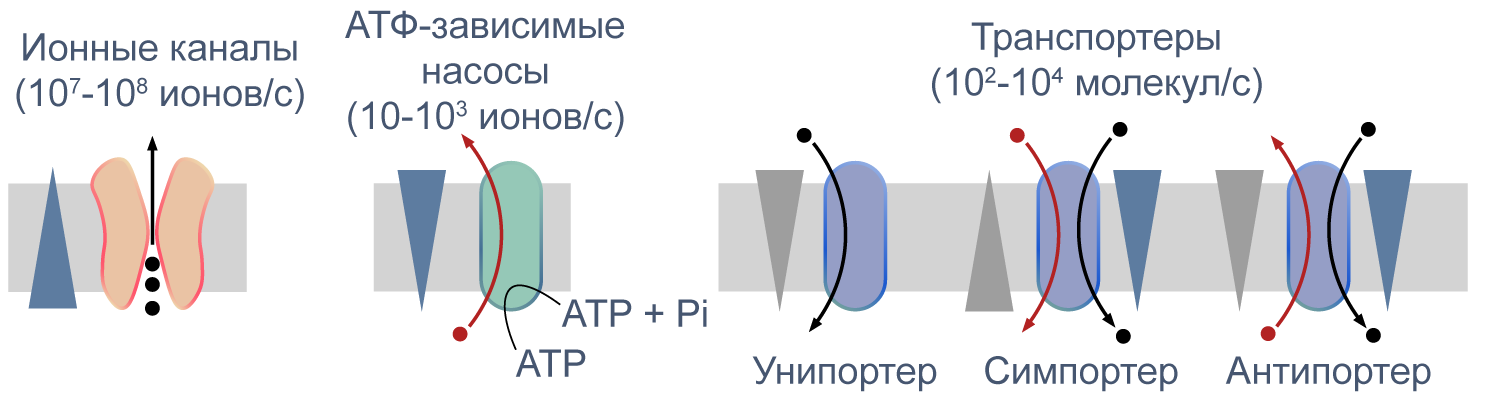
Процессы транспорта веществ через мембрану можно классифицировать по источнику энергии для транспорта. Пассивный транспорт — это движение вещества через канал или транспортер по градиенту концентрации*, то есть за счет энергии электрохимического градиента. Таким способом через калиевые каналы пассивно движутся ионы калия, или осуществляется перенос глюкозы через транспортер GLUT4 (такой тип транспорта еще называют облегченной диффузией, а транспортеры, переносящие только один субстрат — унипортерами). Кроме пассивного транспорта, существует активный транспорт, при котором субстраты переносятся против градиента концентрации с затратой энергии, запасенной клеткой в виде АТФ (например, Na/K-АТФаза).

Некоторые транспортеры сопрягают перенос ионов или молекул против градиента концентрации с движением ионов по градиенту концентрации. Симпортеры переносят различные частицы в одном направлении (например, KCC2 — K—Cl cotransporter 2 — K/Cl котранспортер 2), а антипортеры, или обменники, — в противоположных (например, NHE-1 — Na/H exchanger 1 — Na/H обменник, участвующий в поддержании клеточного pH). Такой транспорт называется вторично-активным.

Рисунок 5 | Пассивный и активный транспорт веществ через мембрану. Треугольниками показаны концентрационные градиенты. Черными стрелками показано движение по градиенту концентрации, красными — против градиента концентрации. По [13], с изменениями.

В старой литературе можно встретить концепцию «белков-переносчиков»: до открытия молекулярной идентичности многих каналов и транспортеров (т. е. какая молекула опосредует данный ионный ток и какой ген ее кодирует) существовало представление о переносчиках как о челноках, связывающих субстраты с одной стороны мембраны, диффундирующих через мембрану и высвобождающих субстраты с другой стороны. Однако, когда стали известны аминокислотные последовательности транспортных белков, стало понятно, что все они часто содержат многочисленные трансмембранные домены и образуют сквозной путь через мембрану.

Различия между каналами, транспортерами и насосами заключаются в механизме их работы и регуляции. Каналы представляют собой более или менее селективную пору, через которую ионы могут свободно диффундировать, не вызывая конформационных изменений в белке канала. При токе через отдельный канал в 1 пА по нему проходят 6×10⁶ одновалентных ионов в секунду. Транспортер, связываясь с субстратом, изменяет свою конформацию для переноса субстрата. При ко-транспорте повышается аффинность транспортера в новой конформации к второму субстрату, и субстраты переносятся через мембрану сопряженно. Насосы, также называемые АТФазами, (ауто)фосфорилируются АТФ, и это фосфорилирование значительно изменяет их конформацию и приводит к транслокации субстратов через мембрану. Электрическая проводимость насосов очень мала: Na/K-АТФаза переносит всего около 300 Na⁺ и 200 K⁺ в секунду.

Граница между молекулами каналов и транспортеров не всегда строга. Например, семейство хлоридных каналов и транспортеров ClC (англ. Chloride Channel) включает в себя гомологичные друг другу каналы (ClC-1, 2, Ka и Kb) и Cl/H-обменники (ClC-3–7), которые можно превратить в каналы, внеся мутацию в единственный остаток глутамата (т. н. gating glutamate — воротный глутамат) [14]. Na/K-АТФазу также можно превратить в простую пору, например, с помощью палитоксина^[15]. Хлоридный канал CFTR относится к группе ABC-транспортеров, однако он использует энергию АТФ не для транспорта ионов, а для регуляции открытия и закрытия канала^[16]. Кроме того, существуют данные о том, что везикулярный транспортер глутамата VGLUT1 кроме обмена глутамата на протоны также опосредует не сопряженный с обменом ток Cl^{− [17]}.

Клеточная мембрана как электрическая цепь

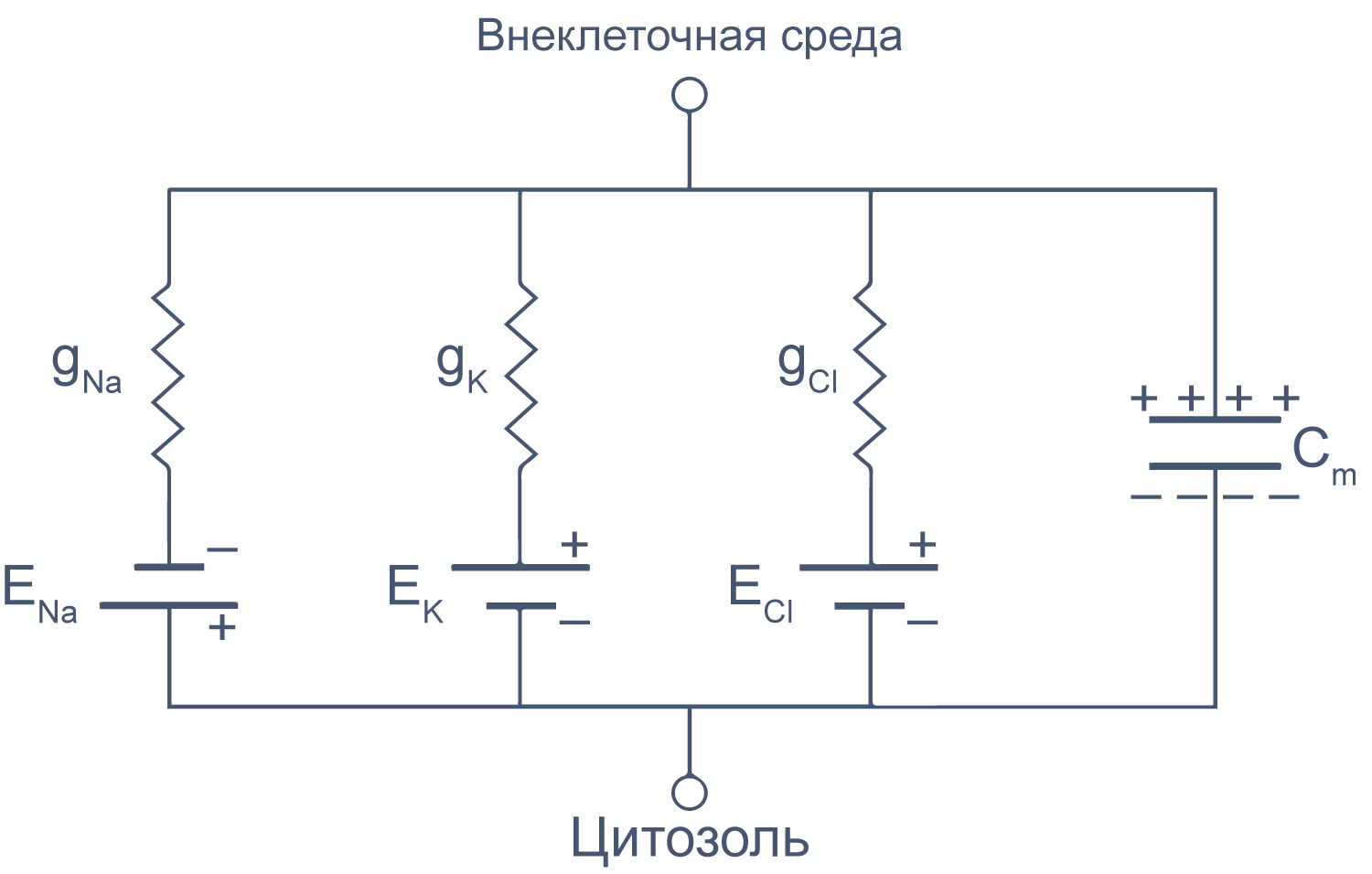
Липидный бислой мембраны можно представить как резистор (сопротивление) и конденсатор (емкость), соединенные параллельно. Величина сопротивления зависит от плотности каналов в мембране и их функционального состояния. Электроемкость возникает из-за разделения зарядов по обе стороны мембраны тонким слоем диэлектрика (гидрофобными хвостами фосфолипидов).

Рисунок 6 | Плазматическая мембрана, представленная в виде RC схемы. g_Na, g_K, g_Cl — проводимость** мембраны для ионов Na⁺, K⁺ и Cl^–, соответственно; E_Na, E_K, E_Cl — электродвижущая сила, или равновесные потенциалы для соответствующих ионов, С_m — электроемкость мембраны.

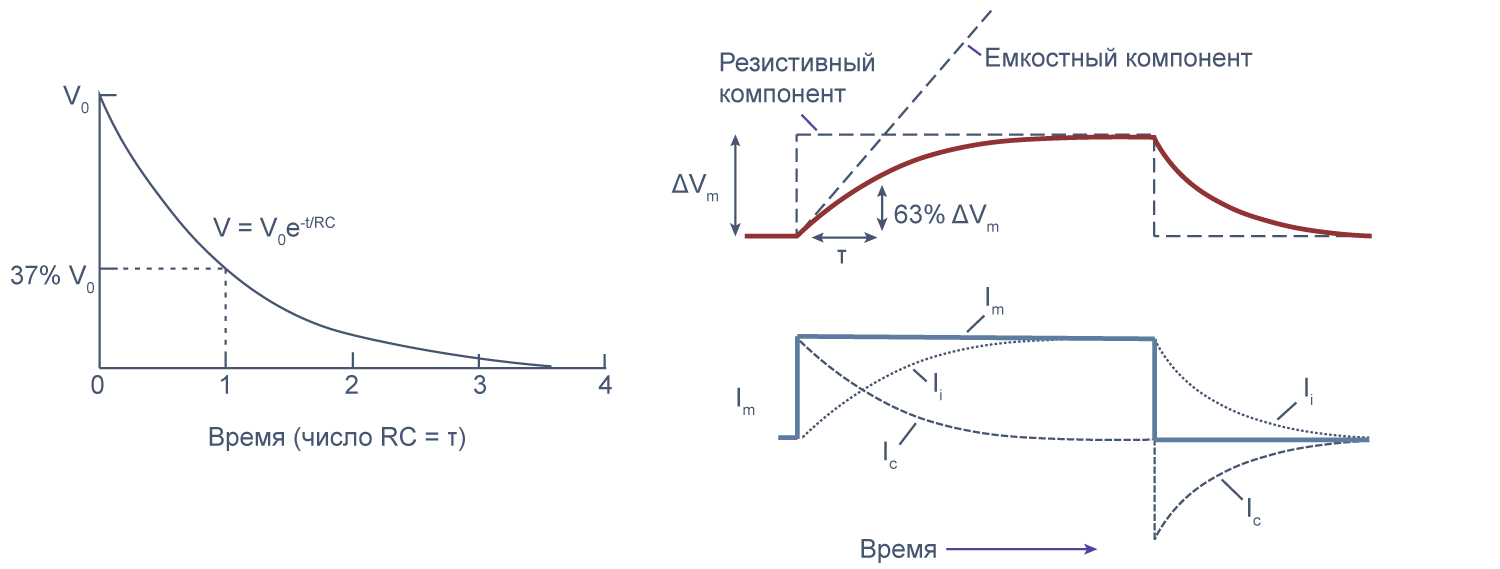
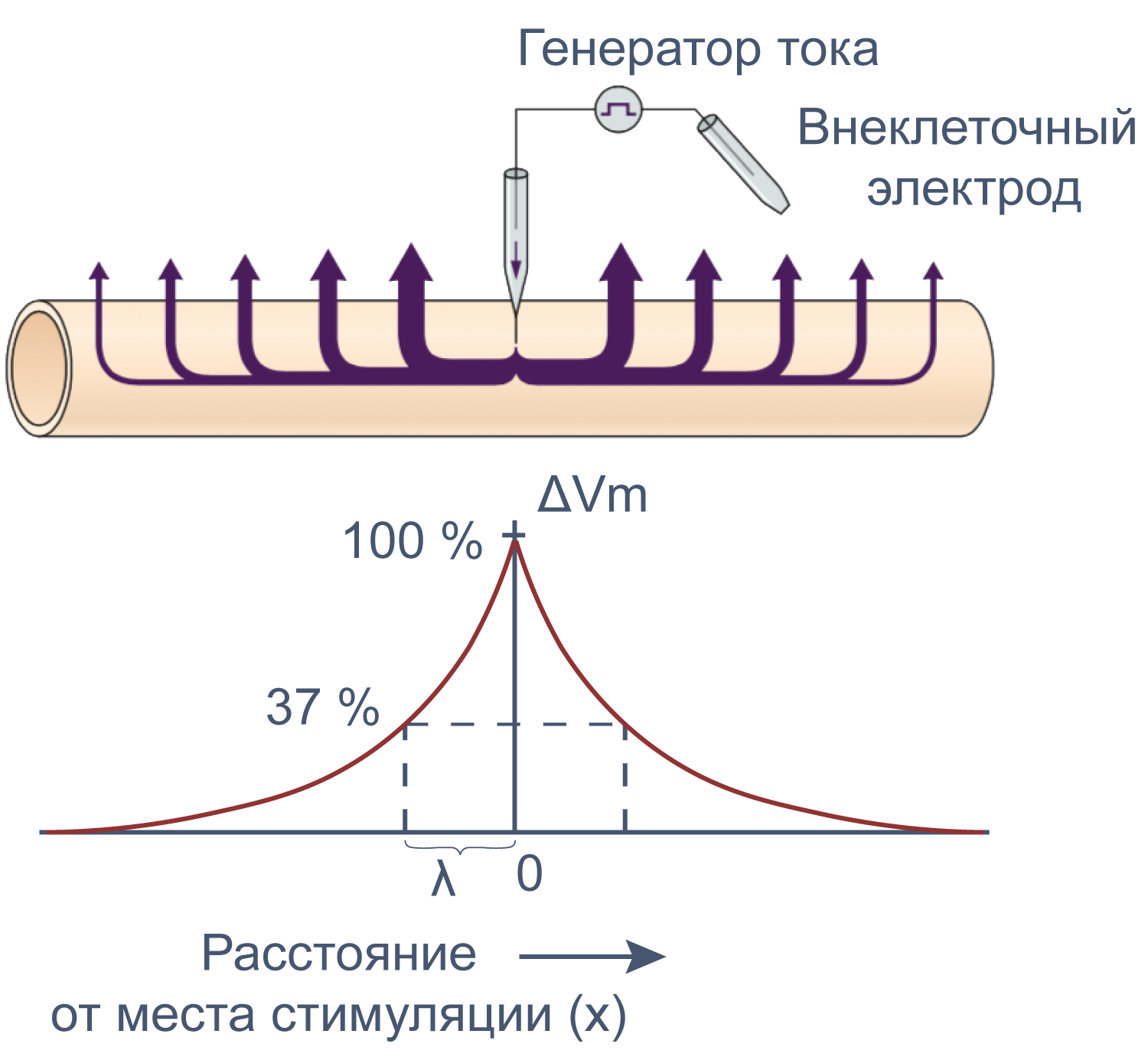
Можно считать, что проводимость (величина, обратная сопротивлению, измеряемая в сименсах) характеризует проницаемые для ионов компоненты структуры мембраны, а емкость — не проницаемые для ионов структуры. Удельная емкость мембраны составляет приблизительно 1 мкФ/см² или 0,01 пФ/мкм²*** и мало зависит от типа клеток^[2]. Это позволяет оценить размер клетки по ее электрическим характеристикам. Высокая электроемкость клеточных мембран задерживает изменения потенциала в ответ на ток. Эту задержку можно выразить через постоянную времени τ, которая равна произведению емкости и параллельно соединенного с ней сопротивления (RC). Если конденсатор зарядить на некоторую величину, а затем дать ему разрядиться через резистор, то потенциал будет убывать экспоненциально согласно формуле V = V₀e^–t/RC, то есть за каждые τ = RC секунд потенциал будет падать в 1/e раз (на 37 % от исходной величины). Этот расчет применим и к клеточной мембране: падение напряжения при разрядке мембраны будет подчиняться экспоненциальному закону. То есть, если приложить гипер- или деполяризующий стимул, то мембранный потенциал через время τ достигнет 63 % конечного сдвига.

Рисунок 7 | Падение напряжения при разрядке мембраны. Изменение мембранного потенциала при деполяризации мембраны на ΔV_m ^[22], I_c — емкостный ток, I_i — ионный ток, I_m — суммарный ток через мембрану. Пояснения в тексте.

Потенциал действия 

Возбудимые клетки могут быстро изменять потенциал на мембране и этим запускать внутриклеточные процессы, например, мышечное сокращение или экзоцитоз везикул. Кратковременный локальный скачок мембранного потенциала от приблизительно –80 мВ (значения потенциала покоя) до 0…+20 мВ за счет изменения проницаемости мембраны для ионов называется потенциалом действия.

Для начала рассмотрим потенциал действия в аксонах нейрона на примере гигантского аксона кальмара. Выбор столь экзотического объекта обусловлен историческими причинами. Современная микроэлектродная техника — использование тонких стеклянных микропипеток, заполненных раствором электролита, — была предложена лишь в 1949 году Дж. Лингом и Р. Джерардом^[18]. До этого поместить электрод, представлявший собой тонкую проволоку, внутрь клетки, не разрушив ее, можно было только в случае ее крупных размеров. Гигантский аксон кальмара стал идеальным модельным объектом для изучения потенциала действия: его диаметр может достигать 0,5–1 мм. Этот отросток служит для быстрой передачи нервных импульсов у беспозвоночных, у которых отсутствует миелинизация. Внутренним содержимым аксона легко манипулировать, заменяя ионный состав внутриклеточного раствора, а внутрь такого аксона можно поместить электрод для регистрации мембранного потенциала.

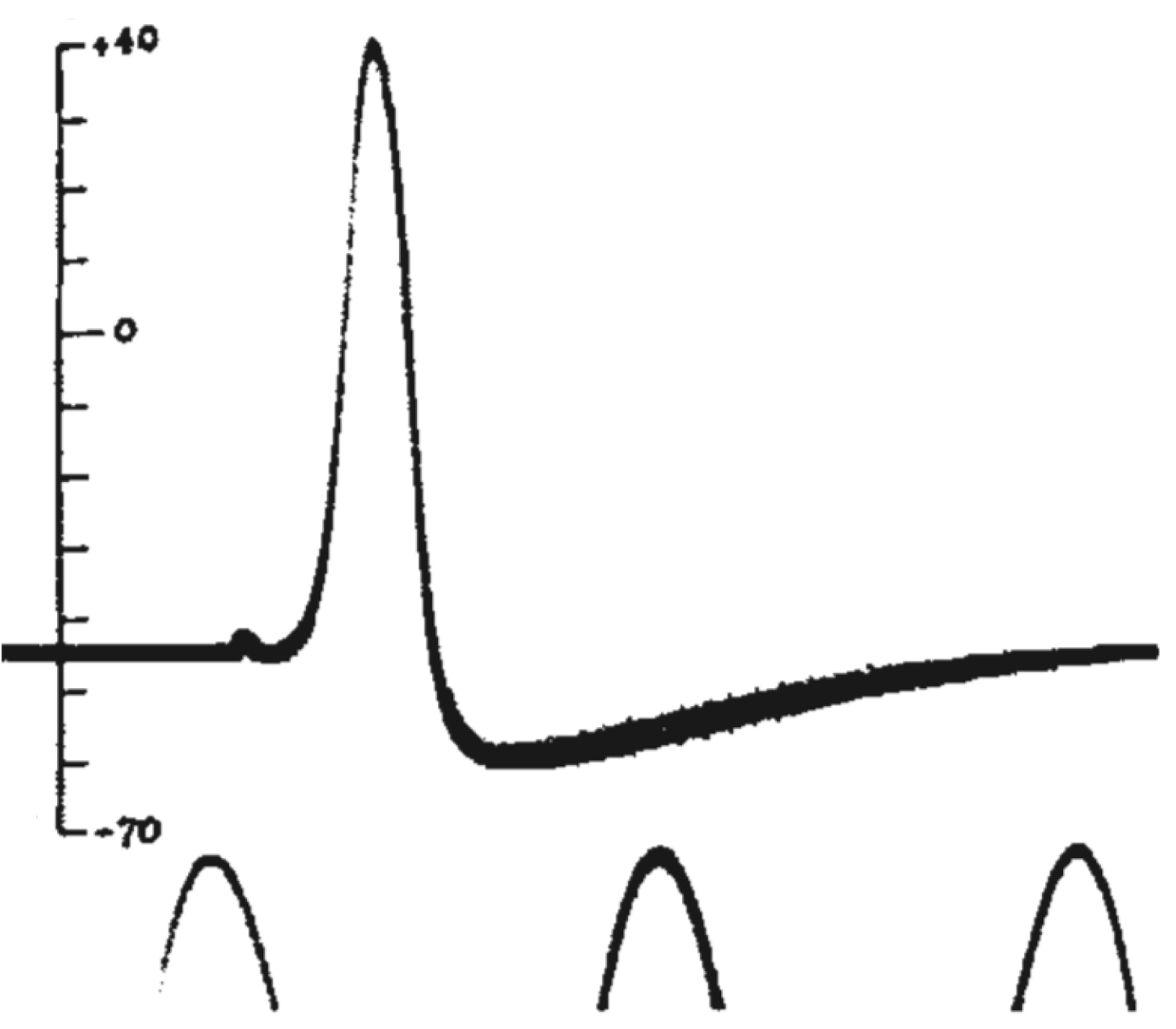
Так, в 1939 году А. Ходжкин и Э. Хаксли опубликовали в журнале Nature короткую заметку «Потенциалы действия, зарегистрированные внутри нервного волокна»^[19], в которой они описали первый эксперимент по внутриклеточному измерению мембранного потенциала на гигантском аксоне кальмара. Посмотрим на потенциалы действия, которые зарегистрировали исследователи.

Рисунок 8 | Потенциал действия из статьи А. Ходжкина и Э. Хаксли 1939 года^[19]. Потенциал действия был зарегистрирован как разность потенциала между внутренней средой аксона и внешней средой. Пики внизу рисунка — это фрагменты синусоидального сигнала с частотой 500 Гц. Вертикальной чертой отмечен потенциал внутреннего электрода в милливольтах, потенциал морской воды снаружи аксона был принят за ноль.

Мы видим резкую деполяризацию мембраны до положительных значений, а затем более плавное возвращение потенциала к отрицательным значениям, зачастую более отрицательным, чем величина потенциала покоя. Из этих наблюдений следовало два важных вывода: 1) потенциал действия генерируется мембраной клетки, что не было очевидно в 1930-е годы; 2) поскольку измеренная амплитуда потенциала действия была больше величины мембранного потенциала, генерация потенциала действия — это активный процесс, который нельзя объяснить временным «пробоем» в мембране (каким бы наивным такое представление нам не казалось сегодня, в 1930-е так думали многие физиологи). В том же году К. С. Коул и Х. Дж. Кертис^[20] зарегистрировали кратковременное изменение проводимости мембраны с 1 мСм/см² до 40 мСм/см² при генерации потенциала действия. Эти данные также свидетельствовали о тонкой регуляции этого процесса.

После Второй мировой войны Ходжкин и Хаксли вернулись к своим исследованиям. В 1945 году они опубликовали статью с несколькими дополнительными экспериментами, подтверждающими сформулированные ранее выводы. Но и тогда ионные механизмы потенциала действия оставались неясными.

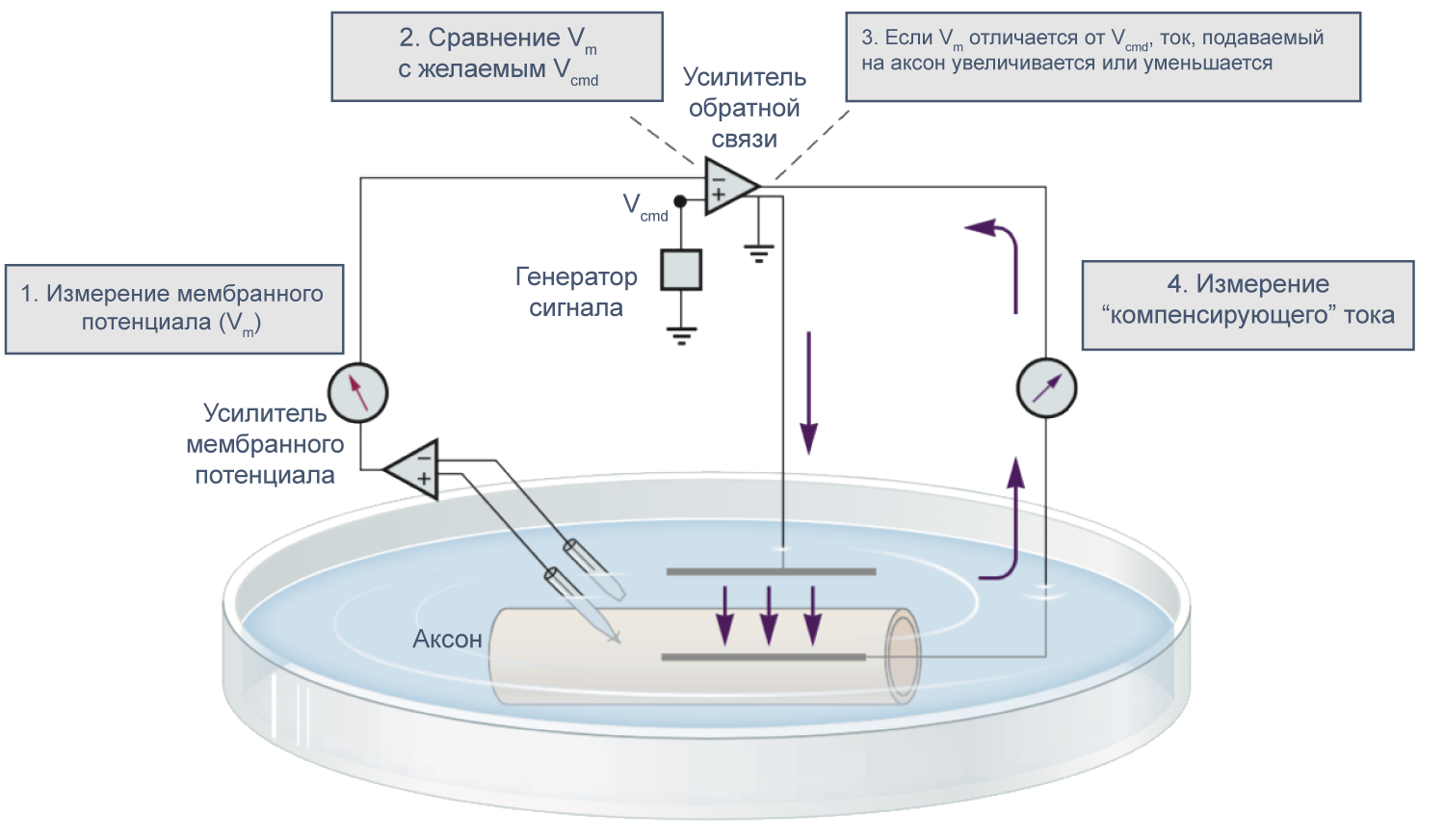
В 1952 году вышла серия статей, посвященных разгадке механизма генерации потенциала действия. Ведущую роль в этом открытии сыграл новый метод фиксации потенциала с помощью двух электродов (в англоязычной литературе TEVC — two-electrode voltage clamp), разработанный в конце 1940-х годов К. С. Коулом и Дж. Мармонтом^[21]. Этот метод позволяет измерять не только потенциал, но и токи при заданном значении мембранного потенциала. Как же осуществляется фиксация потенциала с помощью двух электродов на заданном уровне (V_cmd — «командный потенциал»)? В клетку помещают два электрода, один из которых измеряет потенциал (относительно внеклеточного электрода сравнения) и передает его значение на специальный усилитель, который сравнивает измеренный потенциал со значением командного потенциала. Это устройство вычисляет ток, необходимый для компенсации этой разницы, и подает через второй внутриклеточный электрод ток такой величины, чтобы потенциал на мембране клетки стал равен V_cmd (V_m = V_cmd). Из амплитуды тока, необходимого для компенсации сдвига потенциала до V_cmd, можно сделать вывод о токе через мембрану при данном значении мембранного потенциала. Ток при данном значении потенциала равен току, подаваемому на второй электрод, взятому с обратным знаком.

Рисунок 9 | Схема фиксации потенциала с помощью двух электродов^[21].

В 1970–80-х годах Эрвин Неер и Берт Сакман (Erwin Neher, Bert Sakmann) предложили метод локальной фиксации потенциала (англ. patch clamp), позволяющий работать с мелкими клетками и токами малой амплитуды и даже регистрировать активность отдельных каналов. Тем не менее, метод фиксации потенциала двумя электродами в микроэлектродной конфигурации используется и сегодня при работе с такими крупными клетками, как ооциты лягушки Xenopus laevis.

Временной ход потенциала действия

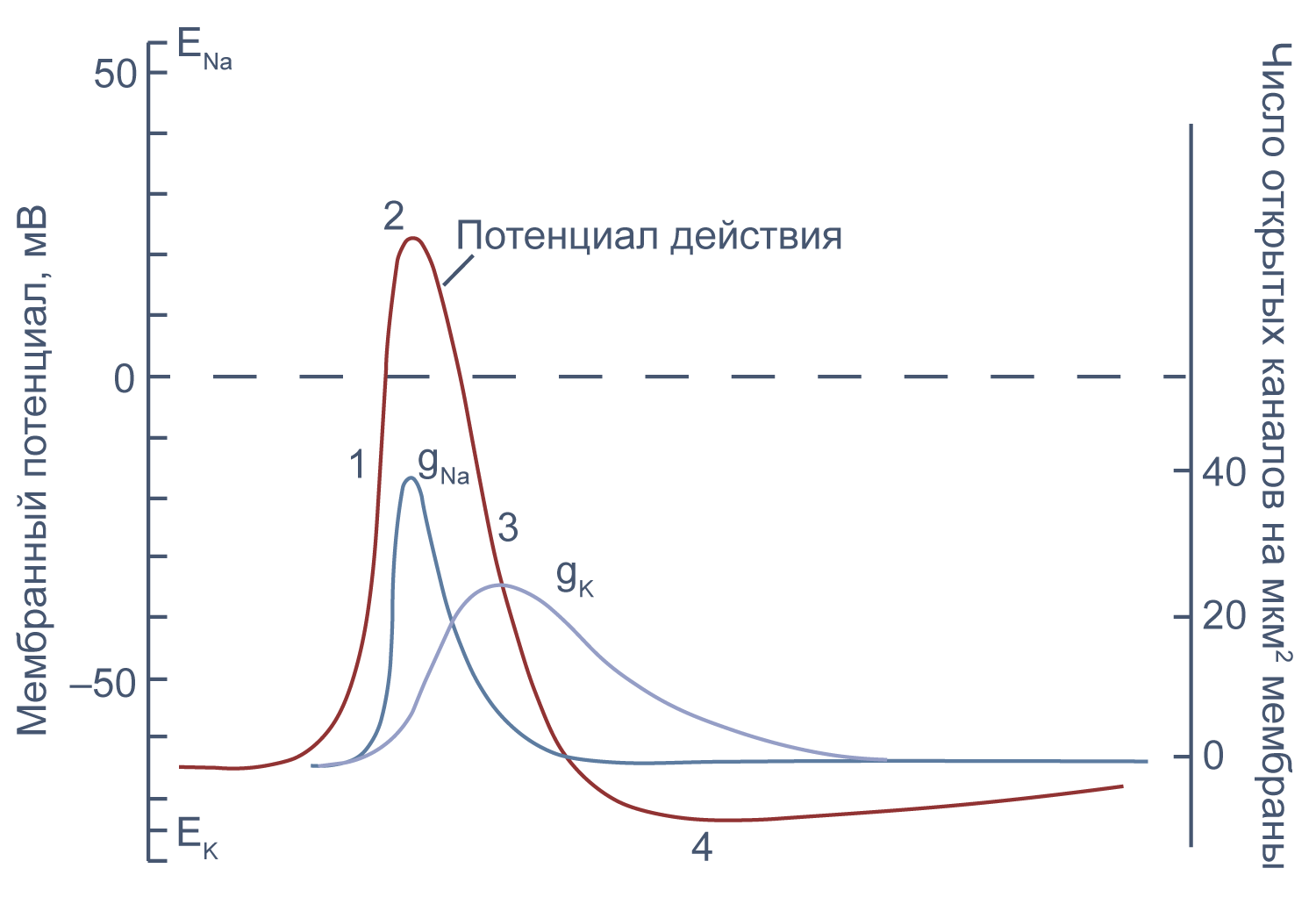
Потенциал действия в аксоне можно разделить на 1) фазу быстрой деполяризации до 2) положительных значений (овершута, от англ. overshoot), 3) фазу реполяризации, в которой потенциал возвращается к потенциалу покоя или даже до несколько более отрицательных значений — 4) следовая гиперполяризация.

Рисунок 10 | Потенциал действия и изменения проводимости мембраны для Na⁺ и K⁺ в гигантском аксоне кальмара. Из [22], с изменениями.

Изменяя ионный состав внутри- и внеклеточного раствора, можно изолировать ионные токи, которые опосредуют изменение мембранного потенциала при потенциале действия. Так, помещая аксон в раствор, в котором натрий заменен на холин, можно изолировать натриевый и калиевый компонент потенциала действия, то есть отдельно измерить калиевый ток^[20]. Этого же можно достичь применением блокаторов потенциал-зависимых натриевых и калиевых каналов — тетродотоксина и тетраэтиламмония (TEA).

Чтобы понять взаимосвязь ионных токов и вызванных ими изменений потенциала, рассмотрим всю цепь событий при генерации потенциала действия. Сначала мембрана деполяризуется под действием внешнего стимула: поступления в клетку катионов через лиганд-управляемые каналы, закрытия калиевых каналов или электрической стимуляции в эксперименте. Если деполяризация достигает порогового значения для потенциалзависимых натриевых каналов (Na_v), они открываются, натрий по градиенту своей концентрации входит в клетку, и мембрана деполяризуется еще сильнее. Дальнейшая деполяризация влечет за собой лавинообразное открытие все новых натриевых каналов, ток через которые приводит к еще большей деполяризации. Однако эта петля положительной обратной связи не работает бесконечно: открывшись на некоторое время, натриевые каналы инактивируются и не могут открыться вновь, пока мембранный потенциал не вернется к отрицательным значениям.

Механизм инактивации был предложен еще в математической модели Ходжкина и Хаксли^[23] на основании кинетических характеристик тока. Они предположили, что в натриевом канале есть три активационные частицы m и одна инактивационная частица h. Когда стала известна аминокислотная последовательность канала, выяснилось, что канал на самом деле имеет четыре гомологичных активационных домена и один инактивационный, однако один из активационных доменов срабатывает значительно медленнее остальных трех, и его влияние на кинетические характеристики тока маскируется происходящей в то же время инактивацией канала (например, [24]).

В то же время деполяризация мембраны приводит к активации потенциал-зависимых калиевых каналов (K_v), которые открываются медленнее, чем натриевые, калий выходит из клетки, и потенциал возвращается к потенциалу покоя и может даже временно стать более отрицательным: пока натриевые каналы инактивированы, потенциал становится ближе к калиевому равновесному потенциалу, и это явление называется следовой гиперполяризацией.

Генерация потенциала действия происходит по принципу «все или ничего». Если деполяризующий стимул не достиг порогового значения, потенциал действия не генерируется. Если же порог был достигнут, положительная обратная связь обеспечивает открытие всех доступных натриевых каналов, и потенциал действия достигает своей максимальной амплитуды.

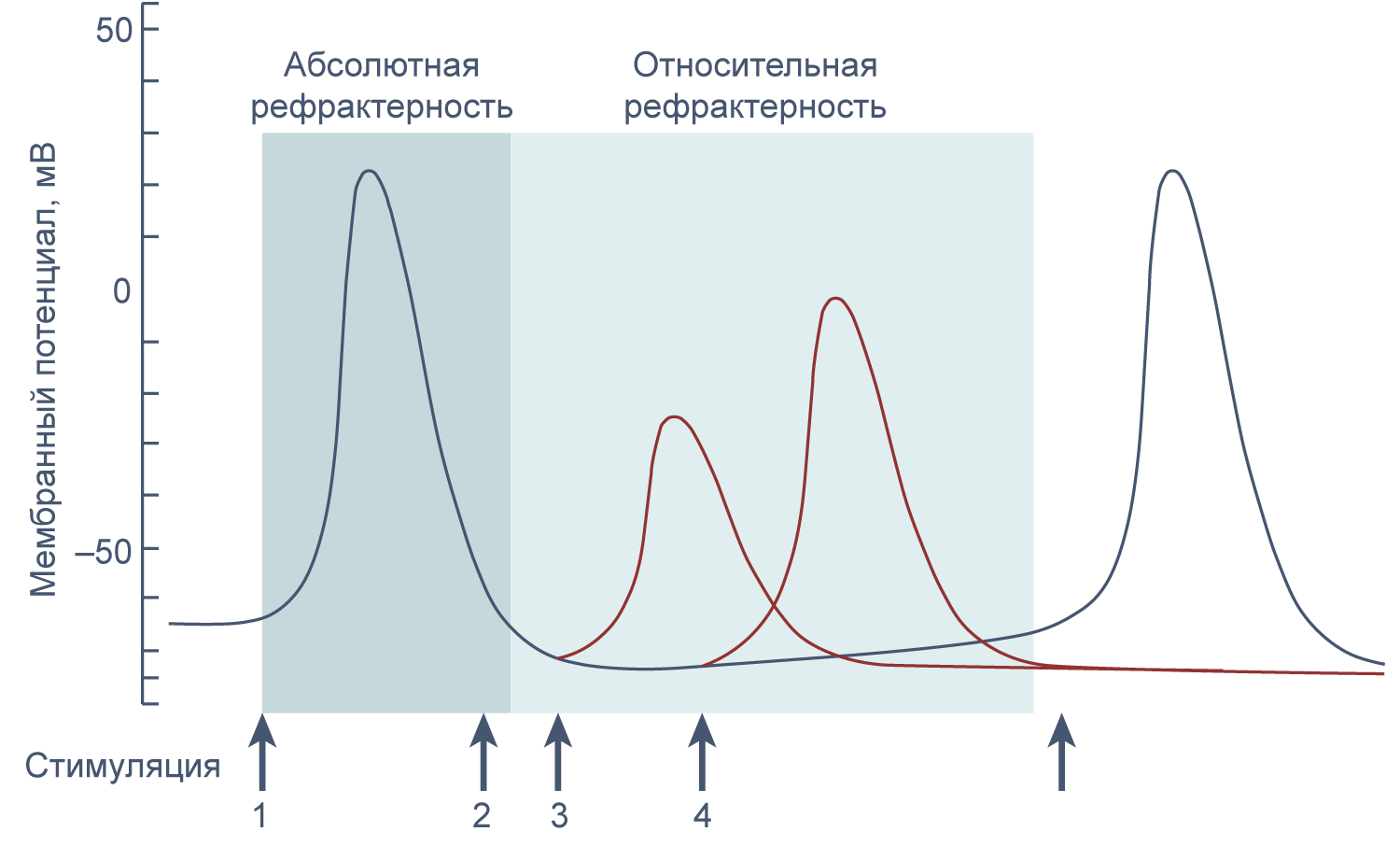
Если новый стимул приходит во время или сразу после генерации потенциала действия, второй потенциал действия не возникает или обладает меньшей амплитудой, чем первый. Это явление называется рефрактерностью. Стимул, возникший в период абсолютной рефрактерности, не вызывает генерации потенциала действия, а пришедшийся на период относительной рефрактерности вызывает потенциал действия уменьшенной амплитуды, так как часть натриевых каналов все еще инактивирована.

Рисунок 11 | Абсолютная и относительная рефрактерность. Стимуляция в период абсолютной рефрактерности (2) не ведет к генерации потенциала действия, а стимуляция в период относительной рефрактерности (3 и 4) приводит к генерации потенциала действия сниженной амплитуды.

Стоит отметить, что внутриклеточная концентрация физиологически значимых ионов при генерации потенциала действия не меняется, и ионные токи задействуют пренебрежимо малую долю от общего числа Na⁺ и K⁺. Это можно проиллюстрировать следующим примером. Рассчитаем число ионов, которое должно пересечь мембрану для деполяризации на 100 мВ. Заряд на мембране равен произведению емкости мембраны и потенциала: Q = C_mV_m. Удельная емкость мембраны близка к 1 мкФ/см², а сдвиг потенциала в нашем случае равен 0,1 В. Тогда количество разделенных зарядов равно Q = 10−6 Ф/см² × 0,1 В = 10−7 Кл/см². Величина заряда одного иона Na⁺ или K⁺ (элементарного заряда) равна 1,6 × 10−19 Кл, тогда количество переносимых через мембрану ионов равно 10−7 Кл/см² / 1,6 × 10−19 Кл = 6,25 × 1011 ионов/см², или 6250 ионов/мкм². Для клетки диаметром 10 мкм площадь поверхности мембраны будет приблизительно равна 4πr² = 314 мкм² (в этом расчете для простоты мы считаем клетку гладкой сферой), а объем — 4πr³/3 = 524 мкм³. При внутриклеточной концентрации Na⁺ 10 мМ, а K⁺ 150 мМ содержание этих ионов в цитозоле будет равно 3,2 × 109 и 4,7 × 1010 соответственно. В течение одного потенциала действия приблизительно 314 мкм² × 6,250 ионов/мкм² ≈ 2 000 000 ионов Na⁺ входит в клетку в фазе деполяризации и примерно столько же ионов K⁺ выходит из клетки в фазе реполяризации, что составляет всего 0,06 % от общего числа ионов натрия в клетке. Токи такой величины обычно не изменяют макроскопические концентрации ионов в клетке, поскольку работа Na/K-АТФазы компенсирует эти незначительные изменения. Однако при определенных условиях концентрации Na⁺ и K⁺ все же могут измениться, например, при продолжительной стимуляции аксонов с малым диаметром^[25].

Распространение возбуждения по аксону

Электрические свойства мембраны помогают понять изменения мембранного потенциала не только во времени, но и в пространстве. Пассивное, или электротоническое распространение возбуждения по мембране происходит без изменения проводимости потенциал-зависимых каналов. Для распространения потенциала действия важен как активный (изменение проводимости натриевых и калиевых каналов), так и пассивный механизмы, поскольку деполяризация, вызывающая открытие новых потенциал-зависимых натриевых каналов, должна достигнуть нового невозбужденного участка аксона, и происходит это благодаря электротоническому распространению возбуждения.

Рисунок 12 | Электротоническое распространение возбуждения. Пояснения в тексте [22].

Сдвиг потенциала в точке, отстоящий на x от места стимуляции, можно вычислить как E_x = E₀e^–x/λ, где E₀ — это сдвиг потенциала в точке стимуляции, а λ — постоянная длины.

Постоянная длины возрастает с увеличением сопротивления мембраны (r_m) и уменьшается с возрастанием сопротивления аксоплазмы (r_i), которое в свою очередь зависит от концентрации подвижных зарядов в объеме аксона. Знание этих закономерностей позволяет понять зависимость скорости распространения возбуждения от радиуса (R) аксона. Сопротивление мембраны r_m пропорционально 1/2πR, сопротивление аксоплазмы r_i — 1/πR², а емкость мембраны C_m пропорциональна R. По мере увеличения радиуса аксона и r_m, и r_i уменьшаются, но r_i уменьшается сильнее. Постоянная длины увеличивается, следовательно, сдвиг потенциала может распространяться по более крупному аксону дальше. Кроме того, увеличение радиуса аксона ведет к увеличению емкости мембраны, однако этот эффект нивелируется тем, что емкость с увеличением радиуса растет линейно, а уменьшение r_i пропорционально квадрату радиуса. Таким образом, проводимость аксоплазмы увеличивается быстрее (при снижении r_i), чем растет емкость мембраны, и это позволяет току быстрее достигать невозбужденных участков мембраны более крупного аксона.

Зависимость скорости распространения потенциала действия по аксону от его диаметра объясняет необходимость в гигантских аксонах у кальмара. Однако у позвоночных гигантских аксонов нет, и достаточная скорость проведения нервных импульсов достигается с помощью миелинизации аксонов. Миелиновые оболочки образованы специальными глиальными клетками: олигодендроцитами в центральной нервной системе и клетками Шванна в периферической. Эти клетки оборачивают аксон, образуя вокруг него плотный чехол из десятков слоев плазматической мембраны, который работает как изолятор. Под миелиновой оболочкой очень мало или почти нет натриевых каналов. Они оказываются расположены на небольших участках мембраны аксона между двумя соседними шванновскими клетками или олигодендроцитами — в перехватах Ранвье. Миелиновая оболочка увеличивает скорость проведения потенциала действия благодаря повышению сопротивления мембраны r_m. При этом снижаются потери тока через мембрану, и деполяризация может пассивно распространяться на бо́льшие расстояния. Кроме того, из-за снижения емкости мембраны C_m, меньшая доля тока тратится на перезарядку мембраны. Миелинизация делает передачу потенциала действия не только быстрее, но и эффективнее, поскольку натриевые каналы располагаются только в перехватах Ранвье, благодаря чему меньшее количество ионов натрия входит в клетку и меньше энергии требуется на работу Na/K АТФ-азы для поддержания концентрационного градиента.

Потенциалы действия в других возбудимых клетках

Минималистичный натриево-калиевый потенциал действия характерен только для аксонов нейронов. В других частях нейрона и в иных типах возбудимых клеток в генерации потенциала действия принимают участие разнообразные ионные каналы, в том числе калиевые каналы других семейств и кальциевые каналы плазматической мембраны и эндоплазматического ретикулума (ЭПР является внутриклеточным депо кальция; общая концентрация Ca²⁺ в нем достигает миллимолярных значений, а концентрация свободного кальция находится в микромолярном диапазоне^[26]; эти значения на несколько порядков выше, чем 100 нМ свободного Ca²⁺ в цитозоле в состоянии покоя). Различия в экспрессии генов ионных каналов в различных типах возбудимых клеток порождают разнообразие потенциалов действия, различающихся ионными механизмами, длительностью (от 1,5 мс в аксонах до 500 мс в кардиомиоцитах желудочков), необходимостью внешнего стимула для генерации или наличием собственного ритма. Многие ионные каналы, не участвуя напрямую в генерации потенциала действия, влияют на возбудимость клеток и таким образом вносят вклад в разнообразие электрической активности клеток.

* Принятое в физиологической литературе употребление фраз «по» или «против градиента концентрации» расходится с физическим понятием градиента. В математике и физике градиент направлен в сторону наибольшей скорости возрастания функции или величины; так, если вещество движется в направлении этого вектора, то физиологи говорят о движении «против градиента концентрации», а если в противоположном направлении — то «по градиенту концентрации». Такое словоупотребление прочно закрепилось в литературе, но пусть оно не сбивает вас с толку, когда вы размышляете, откуда взялся минус перед градиентом концентрации в уравнении диффузионного потока (уравнении Фика): J = — D dC/dx, где J — диффузионный поток [моль∙см^-2∙с^-1], D — коэффициент диффузии [см²∙с^-1], а dC/dx— градиент концентрации.

** Проводимость (g = 1/R) — это характеристика скорости движения любых зарядов через мембрану, а проницаемость (P) отражает, насколько легко частицы могут двигаться через мембрану независимо от того, движутся они или нет. Для ионов эти величины связаны. Например, в фазе быстрой деполяризации при потенциале действия возрастает как проводимость, так и проницаемость мембраны для ионов натрия. Однако зачастую, если проницаемость канала для какого-то иона высока из-за высокого сродства участков поры канала для этого иона, такие ионы будут двигаться через канал медленнее, и проводимость будет ниже, чем для других ионов, для которых канал менее проницаем.

*** Удельная емкость чистого липидного бислоя составляет около 0,8 мкФ/см², разница между электроемкостью мембраны и липидного бислоя возникает из-за обилия встроенных в мембрану белков.

Библиография

1. Hediger M.A. et al. The ABCs of membrane transporters in health and disease (SLC series): Introduction // Mol. Aspects Med. 2013. Vol. 34. P. 95–107.
2.  Hille B. Ion Channels of Excitable Membranes. Third edit. Sinauer Associates, Inc., 2001.
3. Caterina M.J. et al. The capsaicin receptor: A heat-activated ion channel in the pain pathway // Nature. 1997. Vol. 389, № 6653. P. 816–824.
4. Jordt S.-E., Tominaga M., Julius D. Acid potentiation of the capsaicin receptor determined by a key extracellular site // Proc. Natl. Acad. Sci. 2000. Vol. 97, № 14. P. 8134–8139.
5. Smart D. et al. The endogenous lipid anandamide is a full agonist at the human vanilloid receptor (hVR1) // Br. J. Pharmacol. 2000. Vol. 129, № 2. P. 227–230.
6. Nersesyan Y. et al. Oxytocin Modulates Nociception as an Agonist of Pain-Sensing TRPV1 // Cell Rep. 2017. Vol. 21, № 6. P. 1681–1691.
7. Berkovic S.F. et al. Human epilepsies: interaction of genetic and acquired factors // Trends Neurosci. 2006. Vol. 29, № 7. P. 391–397.
8. Welsh M.J., Smith A.E. Molecular mechanisms of CFTR chloride channel dysfunction in cystic fibrosis // Cell. 1993. Vol. 73, № 7. P. 1251–1254.
9. Ruan Y., Liu N., Priori S.G. Sodium channel mutations and arrhythmias // Nat. Rev. Cardiol. 2009. Vol. 6, № 5. P. 337–348.
10. Giudicessi J.R., Ackerman M.J. Potassium-channel mutations and cardiac arrhythmias — Diagnosis and therapy // Nat. Rev. Cardiol. Nature Publishing Group, 2012. Vol. 9, № 6. P. 319–332.
11. Thomas R.C. Electrogenic sodium pump in nerve and muscle cells // Am. J. Physiol. 1972. Vol. 52, № 3. P. 563–594.
12. Morth J.P. et al. Crystal structure of the sodium-potassium pump // Nature. 2007. Vol. 450, № 7172. P. 1043–1049.
13. Lodish H. et al. Molecular Cell Biology (5th edition) // Biochemistry and Molecular Biology Education. 2003.
14. Scheel O. et al. Voltage-dependent electrogenic chloride/proton exchange by endosomal CLC proteins // Nature. 2005. Vol. 436, № 7049. P. 424–427.
15. Artigas P., Gadsby D.C. Ouabain affinity determining residues lie close to the Na/K pump ion pathway. // Proc. Natl. Acad. Sci. U. S. A. 2006. Vol. 103, № 33. P. 12613–12618.
16. Li, C., Ramjeesingh, M., Wang, W., Garami, E., Hewryk, M., Lee, D., Rommens, J. M., Galley, K., Bear, C. E. ATPase Activity of the Cystic Fibrosis Transmembrane Conductance Regulator // Journal of Biological Chemistry. 1996. № 45 (271). P. 28463–28468.
17. Martineau M. et al. VGLUT1 functions as a glutamate/proton exchanger with chloride channel activity in hippocampal glutamatergic synapses // Nat. Commun. Springer US, 2017. Vol. 8, № 1.
18. Ling G., Gerard R.W. The normal membrane potential of frog sartorius fibers // J. Cell. Comp. Physiol. Wiley-Blackwell, 1949. Vol. 34, № 3. P. 383–396.
19. Hodgkin A.L., Huxley A.F. Action potentials recorded from inside a nerve fibre // Nature. 1939. Vol. 144. P. 710–711.
20. Cole K.S., Curtis H.J. Electric Impedance of the Squid Giant Axon During Activity // J. Gen. Physiol. 1939. Vol. 22, № 5. P. 649–670.
21. Cole K.S. Mostly membranes // Annu. Rev. Physiol. 1979. Vol. 41, № 1. P. 1–24.
22. Kandel E.R. et al. Principles of Neural Science. Fifth Edit. The McGraw-Hill Companies, Inc., 2013. 1709 p.
23. Hodgkin A.L., Huxley A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve // J. Physiol. 1952. Vol. 117. P. 500–544.
24. Capes D.L. et al. Domain IV voltage-sensor movement is both sufficient and rate limiting for fast inactivation in sodium channels // J. Gen. Physiol. 2013. Vol. 142, № 2. P. 101–112.
25. http://www.physiologyweb.com/lecture_notes/neuronal_action_potential/neuronal_action_potential_na_and_k_concentrations_do_not_change_during_an_action_potential.html
26. Bygrave F.L., Benedetti A. What is the concentration of calcium ions in the endoplasmic reticulum? // Cell Calcium. Churchill Livingstone, 1996. Vol. 19, № 6. P. 547–551.